Material Sciences
Vol.07 No.01(2017), Article ID:19528,10
pages
10.12677/MS.2017.71011
The Design and Calculation of Optical Anti-Reflected and Reflected Multilayer Film
Songyou Lian1, Yunpeng Yu1, Shunhui Lin1, Gang Lin2, Congkang Xu3, Jiangyong Wang1
1Shantou University, Shantou Guangdong
2Shantou Goworld-Display Co., Ltd., Shantou Guangdong
3Wuxi Shumatianke New Energy Technology Co., Ltd., Wuxi Jiangsu

Received: Dec. 28th, 2016; accepted: Jan. 13th, 2017; published: Jan. 16th, 2017
Copyright © 2017 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
This paper gives a brief introduction about the four methods for the structural design of the optical multilayer films, such as the alternated high and low refractive index method, the symmetrical imitated method, the periodic method and the gradient method. Three methods for calculation of the multilayered optical properties are reviewed, including the recursive method, the Fresnel coefficient matrix method and the characteristic matrix method. These three methods are applied to calculate the reflectivity of the anti-reflected and the reflected multilayer film. By using the recursive method, the reflectivity of the anti-reflected multilayer film is obtained as a function of the film thickness and refractive index.
Keywords:Optical Multilayer Film, Design Concept, Fresnel Formula, The Optical Properties, The Recursive Method

光学增透和增反多层膜的设计与计算
连松友1,余云鹏1,林舜辉1,林钢2,徐从康3,王江涌1
1汕头大学,广东 汕头
2汕头超声显示器有限公司,广东 汕头
3无锡舒玛天科新能源技术有限公司,江苏 无锡

收稿日期:2016年12月28日;录用日期:2017年1月13日;发布日期:2017年1月16日

摘 要
本文概括了四种常用的光学增透和增反多层膜结构的设计理念,如高低折射率交替设计、对称等效法、周期性薄膜设计、渐变式薄膜设计等。总结了计算多层膜光学特性的三种方法,包括递推法、菲涅尔系数矩阵法和特征矩阵法。利用MATLAB程序计算了三种方法典型的增透膜与增反膜的反射率,并且利用递推法,分别以薄膜厚度与折射率为自变量,计算了多层增透膜的反射率。
关键词 :光学多层膜,设计理念,菲涅尔公式,光学特性,递推法

1. 引言
1873年麦克斯韦发表了《论电与磁》,奠定了分析薄膜光学问题的理论基础。1835年以前人们用化学湿选法淀积了银镜膜,这是世界上最早制备的光学薄膜,1930年真空蒸发设备的诞生使制备光学薄膜技术得到了长足的发展,随后光学薄膜得到了越来越广泛的应用,特别是在光通信和信息显示技术方面。了解光学薄膜的特性对我们设计薄膜有着很大的帮助,薄膜的光学特性主要以反射率和透射率为主 [1] [2] [3] 。光学薄膜的设计最初主要采用试凑法、图解法 [4] ,接着又发展了各种优化设计方法,如针形算法、遗传算法、单纯形算法等。80年代导纳矩阵法的出现使得多层膜的光学特性的问题解决更加方便 [5] 。本文先对多层膜光学特性计算及初始结构的设计理念做一个简单的介绍,然后利用MATLAB程序计算了多层增透膜与增反膜的反射率,计算结果表明,三种计算方法得出的结果一致。
2. 初始结构的设计理念
2.1. 高低折射率交替性薄膜
该设计理念是在衬底上交替的镀上高低折射率薄膜。Willey [6] 提出了一个很有用的经验公式,用于估算最低的反射率平均值,和带宽(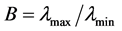 )、膜厚总厚度(T)、最外层薄膜的折射率L、以高低折射率差值(
)、膜厚总厚度(T)、最外层薄膜的折射率L、以高低折射率差值(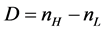 )有关。
)有关。
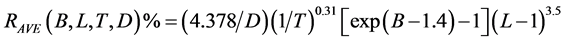 (2.1)
(2.1)
由此公式,Willey指出为实现相当宽波长范围内的增透,必须增加整个膜层的总厚度。而郑臻荣 [7] 等则利用TiO2/MgF2两种材料组成了八层结构的超宽带减反射膜。
2.2. 对称等效性设计
1952年埃普斯坦(L. I. Epstein)首先从数学上对周期性对称膜系进行了分析,并提出了比较完善的等效折射率的概念。单层薄膜的特征矩阵为
 (2.2)
(2.2)
对于多层膜其特征矩阵为各个单层膜的连乘积,考虑三层膜系pqp有
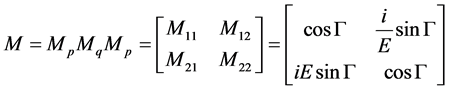 (2.3)
(2.3)
重复这个过程,直到所有膜层都被替换,于是最终又形成一个等效单层膜。若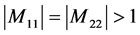 时,等效位相厚度
时,等效位相厚度 是虚数,
是虚数,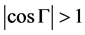 ,
, ,又由式子
,又由式子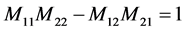 ,知等效折射率
,知等效折射率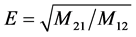 是虚数,这些波段对应膜系的截止带。只有E和
是虚数,这些波段对应膜系的截止带。只有E和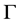 都是实数时,对应的是透射带。唐晋发 [2] 利用对称等效原理,只用高低折射率两种膜料设计了一个39层的反射带宽B达到10的超带宽减反射膜。但是等效折射率通常存在显著的色散,需对薄膜厚度做进一步优化。当给出了高低折射率(
都是实数时,对应的是透射带。唐晋发 [2] 利用对称等效原理,只用高低折射率两种膜料设计了一个39层的反射带宽B达到10的超带宽减反射膜。但是等效折射率通常存在显著的色散,需对薄膜厚度做进一步优化。当给出了高低折射率(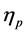 和
和 ),等效折射率E (位于高低折射率的区间范围内)以及位相厚度
),等效折射率E (位于高低折射率的区间范围内)以及位相厚度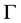 ,即可根据等效特征矩阵求得
,即可根据等效特征矩阵求得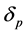 和
和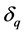 。
。
2.3. 渐变式薄膜设计
理论上渐变折射率薄膜可以设计出满足任何光谱特性的光学薄膜,且渐变式薄膜具有良好的光学致密性以及高的抗激光损伤阈值。对于渐变折射率膜,其实现的基础是共蒸发技术 [8] ,即在成膜时采用两个蒸发源同时蒸发,一个蒸发高折射率膜料,另一个蒸发低折射率膜料。控制两个蒸发源的蒸发速率比,理论上可以得到上述高、低折射率值之间的任意折射率。根据折射率轮廓的不同,可分为褶皱滤光片(图1)、混合渐变膜(图2)、折射率任意变化的光学薄膜(图3),图中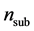 表示基底的折射率,
表示基底的折射率,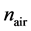 表示空气的折射率。H. Bartzsch用反应脉冲磁控溅射方法制备了440~620 nm的混合渐变增透膜 [9] 。
表示空气的折射率。H. Bartzsch用反应脉冲磁控溅射方法制备了440~620 nm的混合渐变增透膜 [9] 。
B. G. Bovard [10] 指出在渐变折射率介质中,光波的透过率和薄膜折射率轮廓的关系如下
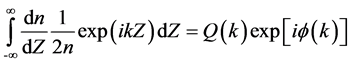 (2.4)
(2.4)
其中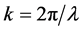 ,
,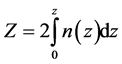 是从薄膜中心到z处的两倍的光程,
是从薄膜中心到z处的两倍的光程,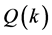 是由光波的透过率
是由光波的透过率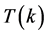 构造的偶函数。式(2.4)中,
构造的偶函数。式(2.4)中,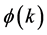 代表位相因子。
代表位相因子。
2.4. 周期性薄膜
目前很多多层减反射膜是由1/4波长层或半波长层构成,可以看做是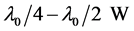 形膜和
形膜和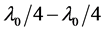 V形膜的改进。对于W形膜,可以将半波长层分成折射率稍微不同的两个
V形膜的改进。对于W形膜,可以将半波长层分成折射率稍微不同的两个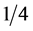 波长层。有利于降低反射率的凸峰 [11] ;也可以在靠近基地处添加一层低折射率的半波长层,以增加低反射区的宽带 [12] ;同样当在V形膜的中间插入半波长的薄膜层,则会使得反射曲线平滑并展宽地反射带的宽度,当用两个折射率代替该半波长膜后,其低反射区的宽带得到进一步的改善 [11] 。如(
波长层。有利于降低反射率的凸峰 [11] ;也可以在靠近基地处添加一层低折射率的半波长层,以增加低反射区的宽带 [12] ;同样当在V形膜的中间插入半波长的薄膜层,则会使得反射曲线平滑并展宽地反射带的宽度,当用两个折射率代替该半波长膜后,其低反射区的宽带得到进一步的改善 [11] 。如(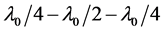 )三层减反射膜结构
)三层减反射膜结构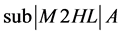 ,其中M为
,其中M为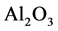 ,H为
,H为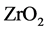 ,L为
,L为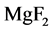 ,其结构如图4所示,其透射率如图5 [13] 。
,其结构如图4所示,其透射率如图5 [13] 。
当将中间的半波长层替换成两个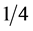 波长的薄膜层厚,典型结构为
波长的薄膜层厚,典型结构为 ,其中L1为
,其中L1为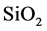 ,M为
,M为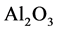 ,H为
,H为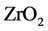 ,L为
,L为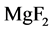 ,其透射率如图6,其透射带得到明显展宽 [13] 。
,其透射率如图6,其透射带得到明显展宽 [13] 。

Figure 1. The refractive index change of fold filter
图1. 褶皱滤光片的折射率变化

Figure 2. The refractive index of a hybrid gradient membrane
图2. 混合渐变膜的折射率

Figure 3. Arbitrary refractive index change of gradient film refractive index
图3. 折射率任意变化的渐变膜的折射率

Figure 4. Diagram of three layers cycle reflected films
图4. 三层周期减反射膜示意图

Figure 5. Transmittance curves of three layers reflected films
图5. 三层周期减反射膜透射率曲线
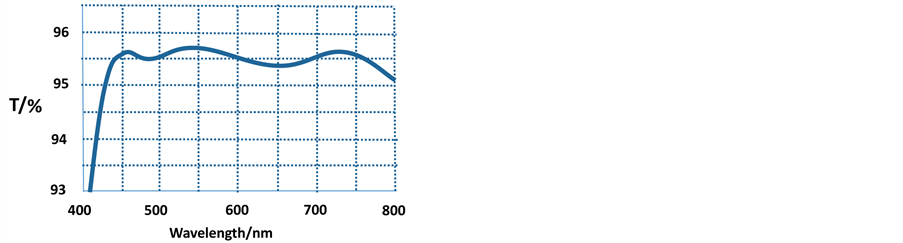
Figure 6. Transmittance curves of four layers cycle reflected films
图6. 四层周期减反射膜透射率曲线
3. 光学特性的确定
3.1. 递推法
单层膜时,光束干涉原理如图7所示,则有
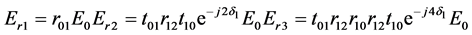
其中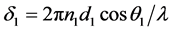 ,
,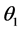 为膜的相位差,
为膜的相位差,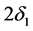 则表示两相邻光束间的相位差。
则表示两相邻光束间的相位差。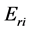 表示反射光。
表示反射光。 和
和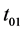 分别表示从第0层(即空气)入射到第1层薄膜的反射系数和透射系数。其和振幅为:
分别表示从第0层(即空气)入射到第1层薄膜的反射系数和透射系数。其和振幅为:
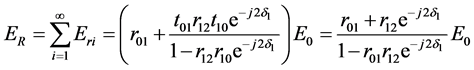 (3.1)
(3.1)
反射系数:
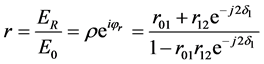 (3.2)
(3.2)
由上面的推导可以看到,薄膜可以等效为一个界面,这个界面的的反射系数为 ,如图8所示。而递推法就是将前面所有膜层等效为一个界面,首先从基底最近的薄膜开始,将薄膜的两个界面等效为一个界面,逐层往上,直至第一个界面,如图9所示。
,如图8所示。而递推法就是将前面所有膜层等效为一个界面,首先从基底最近的薄膜开始,将薄膜的两个界面等效为一个界面,逐层往上,直至第一个界面,如图9所示。
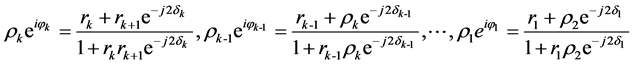
假设各膜层厚度为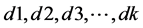 ,入射角为
,入射角为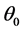 ,由折射定律(
,由折射定律(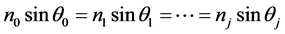 )可得各膜层中光的入射角
)可得各膜层中光的入射角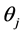 。则在各膜层的间产生的相位差为
。则在各膜层的间产生的相位差为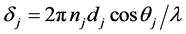 。由菲涅尔系数公式求出各界面的反射透射系数,并用逐次迭代求出由所有薄膜所等效成的一个界面的反射率透射率。
。由菲涅尔系数公式求出各界面的反射透射系数,并用逐次迭代求出由所有薄膜所等效成的一个界面的反射率透射率。

Figure 7. Multiple beam interference figure of single films
图7. 单层膜时多光束干涉图

Figure 8. The equivalent interface figure
图8. 等效界面图
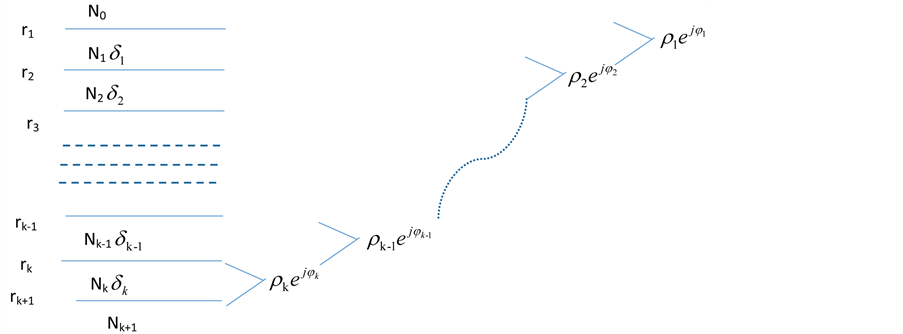
Figure 9. Recursive method to obtain the Fresnel coefficient
图9. 递推法求解菲涅尔系数
在光学薄膜发展的初期阶段,递推法曾经是进行多层薄膜计算的主要方法。随着计算机的发展,矩阵法逐渐取代了递推法。在计算薄膜时,矩阵法分为菲涅尔系数矩阵法和特征矩阵法两种,首先我们介绍菲涅尔系数矩阵方法。
3.2. 菲涅尔系数矩阵确定光学性质
用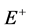 ,
,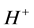 表示正向传播的电场矢量和磁场矢量的切向分量,
表示正向传播的电场矢量和磁场矢量的切向分量, ,
,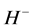 表示反向传播的电场矢量和磁场矢量的切向分量 [12] 。光入射单层膜时,其电场示意图如图10所示,则有
表示反向传播的电场矢量和磁场矢量的切向分量 [12] 。光入射单层膜时,其电场示意图如图10所示,则有
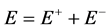 ,
,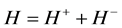 (3.3)
(3.3)
由电磁场的边界连续性条件,以及在同一层膜内侧,靠近上边界与靠近下边界两点间的电磁场复振幅强度仅相差一个位相因子,正向传播时位相因子为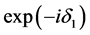 ,负向传播时位相因子为
,负向传播时位相因子为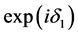 ,可得
,可得
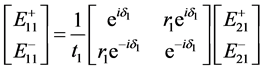 (3.4)
(3.4)

Figure 10. The diagram of the electric field when incident light is perpendicular to the interface (the direction of the arrow is corresponding to the propagation direction of light field. Electric field within 1-2 boundary denotes as E1, down direction of the electric field remembers as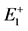 ; the sum of all electric field near the boundary 1 expresses as E11; the sum of all electric field near the border 2 denotes as E12.)
; the sum of all electric field near the boundary 1 expresses as E11; the sum of all electric field near the border 2 denotes as E12.)
图10. 光垂直入射单层膜时的电场表示(箭头的方向是与电场相对应的光的传播方向。在1-2边界内的电场均记为E1,向下记为 ,靠近边界1的所有电场和记为E11,靠近边界2的所有电场和的记为E12)
,靠近边界1的所有电场和记为E11,靠近边界2的所有电场和的记为E12)
依次类推,得
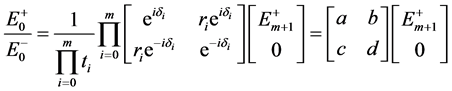 (3.5)
(3.5)
则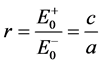 。且有
。且有
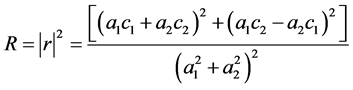 (3.6)
(3.6)
3.3. 特征矩阵法确定多层膜的光学性质
特征矩阵法是用膜层的特征量(如光学厚度,折射率等)来表征薄膜的光学性质。由式(3.3)、(3.4),并结合欧拉公式,可得
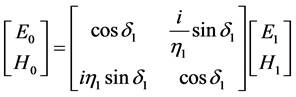 (3.7)
(3.7)
采用递推法,扩展至所有薄膜,则有
 (3.8)
(3.8)
令
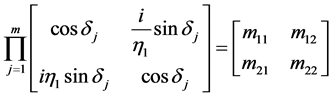 (3.9)
(3.9)
则反射系数为
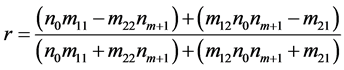 (3.10)
(3.10)
反射率为
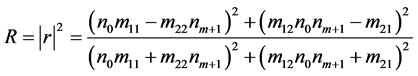 (3.11)
(3.11)
4. 反射率计算示例
4.1. 双层增透膜
我们利用三种多层膜反射率计算方式,通过MATLAB编程,得到了某类典型双层增透膜的反射率。入射光垂直入射时,假设入射光所在媒介折射率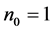 ,基底的折射率为
,基底的折射率为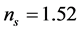 ,薄膜层1 (氟化镁)的折射率
,薄膜层1 (氟化镁)的折射率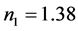 ,厚度为72.46 nm;薄膜层2 (氟化铝)的折射率
,厚度为72.46 nm;薄膜层2 (氟化铝)的折射率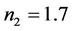 ,厚度为58.82 nm;入射波长为400 nm。三种方法计算得到的反射率均为0.00066%。
,厚度为58.82 nm;入射波长为400 nm。三种方法计算得到的反射率均为0.00066%。
以该增透膜为基础,运用递推法,分别以第一层薄膜厚度、第二层薄膜厚、第一层介质折射率、第二层介质折射率为自变量,其他参数保持不变,求其反射率。发现该增透薄膜的折射率与厚度基本为其最优解。从图11可知,当以第一层膜厚度为自变量时,膜厚取约70 nm时,其反射率具有最低值;当以第二层膜厚为自变量时,从图12可以看出,膜厚取约60 nm时,其反射率具有最低值;当我们以第一层的折射率为自变量时,其反射率与第一层的折射率关系如图13所示,当选择氟化镁时,具有较低的反射率;当以第二层的折射率为自变量时,其反射率与第二层的折射率关系如图14所示,当折射率取值1.7时,也同样具有较低的反射率。

Figure 11. The relationship between the first layer thin film thickness and reflectivity
图11. 反射率与第一层薄膜厚度的关系

Figure 12. The relationship between the second layer thin film thickness and reflectivity
图12. 反射率与第二层薄膜厚度的关系
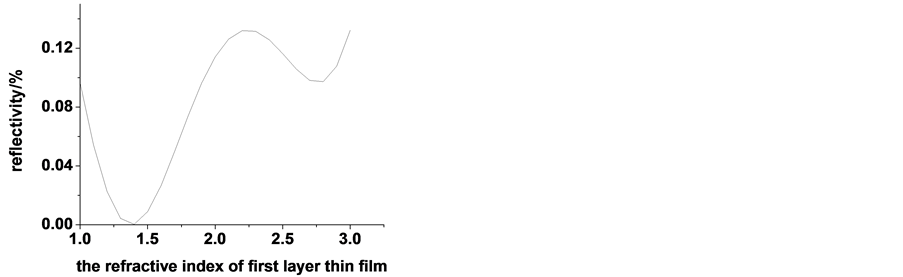
Figure 13. The relationship between the first layer thin film index and reflectivity
图13. 反射率与第一层折射率的关系
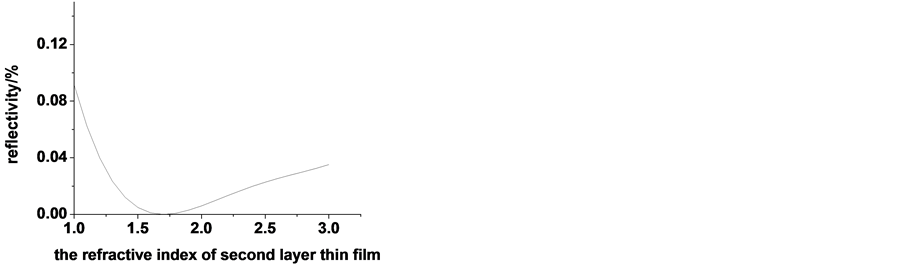
Figure 14. The relationship between second layer thin film index and reflectivity
图14. 反射率与第二层折射率的关系
4.2. 多层增反膜
设入射媒介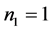 ,基地
,基地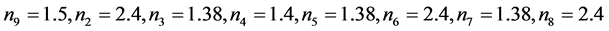 。入射波长为400 nm,薄膜厚度分别为41.68 nm,72.46 nm,41.68 nm,72.46 nm,41.68 nm,72.46 nm,41.68 nm。垂直入射时,用三种方法计算所得反射率均为96.31%。
。入射波长为400 nm,薄膜厚度分别为41.68 nm,72.46 nm,41.68 nm,72.46 nm,41.68 nm,72.46 nm,41.68 nm。垂直入射时,用三种方法计算所得反射率均为96.31%。
同时,本文利用MATLAB编程,以该多层薄膜结构为基础,求解膜厚。膜厚采用周期分布,即d1d2d1d2d1d2d1d2排列,首先令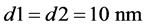 ,然后使d1处于
,然后使d1处于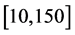 内,以1 nm为波长间距,求出其对应的反射率,得出最大反射率对应的厚度dm1,接着令d1 = dm1,且d2处于
内,以1 nm为波长间距,求出其对应的反射率,得出最大反射率对应的厚度dm1,接着令d1 = dm1,且d2处于 ,求出其对应的反射率,可获得最大反射率对应的厚度dm2,令d2 = dm2。如此反复多次,得到d1 = 42 nm,d2 = 150 nm,反射率为96.3%,该反射率基本与该结构的最佳反射率一致。通过此方法,能够大致求得较佳的膜厚。
,求出其对应的反射率,可获得最大反射率对应的厚度dm2,令d2 = dm2。如此反复多次,得到d1 = 42 nm,d2 = 150 nm,反射率为96.3%,该反射率基本与该结构的最佳反射率一致。通过此方法,能够大致求得较佳的膜厚。
5. 结论
本文利用递推法、菲涅尔系数矩阵法、特征矩阵法三种方法,计算了典型多层增透与增反膜的反射率,对于给定的多层膜结构,三种方法求得的反射率一致。以典型双层增透膜为例,分别以第一层厚度、第一层折射率、第二层厚度、第二层折射率为自变量,计算对应的反射率,验证了其结构的合理性。又以MATLAB程序计算获得了多层增反膜的合理膜厚,其反射率的计算结果与典型增反膜的计算结果基本一样。
文章引用
连松友,余云鹏,林舜辉,林 钢,徐从康,王江涌. 光学增透和增反多层膜的设计与计算
The Design and Calculation of Optical Anti-Reflected and Reflected Multilayer Film[J]. 材料科学, 2017, 07(01): 78-87. http://dx.doi.org/10.12677/MS.2017.71011
参考文献 (References)
- 1. 赵凯华, 钟锡华. 光学[M]. 北京: 北京大学出版社, 1984: 140-330.
- 2. 唐晋发, 郑权. 应用薄膜光学[M]. 上海: 上海科学技术出版社, 1983: 39-67.
- 3. Macleod, H.A. (2001) Thin Film Optical Filter. 3rd Edition, Institute of Physics Publishing, Bristol and Philadelphia, 37-55. https://doi.org/10.1201/9781420033236
- 4. 林永昌, 卢维强. 光学薄膜原理[M]. 北京: 国防工业出版社, 1990: 51-58.
- 5. 唐晋发, 顾培夫, 译. 多层膜设计中的计算机辅助技术[M]. 杭州: 浙江大学出版社, 1984: 9-14.
- 6. Willey, R.R. (1993) Predicting Achievable Design Performance of Broadband Anti-Reflection Coatings. Applied Optics, 32, 5447-5451. https://doi.org/10.1364/AO.32.005447
- 7. 郑臻荣, 顾培夫, 陈海星, 等. 超宽带减反射膜的设计和制备[J]. 光学学报, 2009, 29(7): 2026-2029.
- 8. 沈自才, 王英剑, 范正修, 等. 线性共蒸法制备渐变折射率薄膜的光学特性分析[J]. 中国激光, 2005, 32(6): 829- 834.
- 9. Bartzsch, H. and Lange, S. (2004) Graded Refractive Index Layer Systems for Anti-Reflective Coatings and Rugate Filter Deposited by Reactive Pulse Magnetron Sputtering. Surface & Coatings Technology, 180, 616-620. https://doi.org/10.1016/j.surfcoat.2003.10.105
- 10. Bovard, B.G. (1988) Derivation of a Matrix Describing a Rugate Dielectric Thin-Film. Applied Optics, 27, 1998-2005. https://doi.org/10.1364/AO.27.001998
- 11. 唐晋发, 顾培夫, 刘旭, 等. 现代光学薄膜技术[M]. 杭州: 浙江大学出版社, 2006: 61-81.
- 12. Macleod, H.A. (1986) Thin-Film Optical Filters. 2nd Edition, Adam Hilger Ltd., Bristol, 37-55. https://doi.org/10.1887/0750306882
- 13. 孙英杰. 500~1200 nm宽带减反膜的研制[D]: [硕士学位论文]. 长春: 长春理工大学, 2013: 15-17.