Computer Science and Application
Vol.
08
No.
11
(
2018
), Article ID:
27630
,
6
pages
10.12677/CSA.2018.811190
Application of Predictive Control Algorithm Based on T-S Fuzzy Model in Urban Rail Train Braking Control
Xiaokan Wang, Qiong Wang
Henan Mechanical and Electrical Vocational College, Xinzheng Henan
Received: Oct. 31st, 2018; accepted: Nov. 13th, 2018; published: Nov. 20th, 2018

ABSTRACT
Urban rail transit plays an increasingly important role in modern urban life because of its large carrying capacity, fast speed and zero blockage. Braking system performance directly affects the smoothness and safety of train operation, which is a time-varying, time-delay and nonlinear control system. A predictive control algorithm based on T-S fuzzy model is proposed. The simulation of urban rail train braking control system can realize fast and accurate synchronous braking, overcome the dynamics of uncertainties, hysteresis and time-varying of controlled objects. So it can achieve the desired control objectives and make the system have robust and stable performance.
Keywords:Predictive Control, T-S Fuzzy Model, Urban Rail Train, Algorithm
基于T-S模糊模型的预测控制算法在城轨列车制动控制中的应用
王晓侃,王琼
河南机电职业学院,河南 新郑
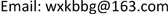
收稿日期:2018年10月31日;录用日期:2018年11月13日;发布日期:2018年11月20日

摘 要
城市轨道交通因其自身载运量大,速度快,零阻塞等诸多优点在现代城市生活中起着越来越重要的作用。制动系统性能直接影响到列车运行的平稳性和安全性,其是一个时变、时滞和非线性的控制系统。提出一种基于T-S模糊模型的预测控制算法,对城轨列车制动控制系统进行仿真,可以实现快速、精确同步制动,从而克服受控对象的不确定性、迟滞和时变等因素的动态影响,从而达到预期的控制目标,并使系统具有良好的鲁棒性和稳定性。
关键词 :预测控制,T-S模糊模型,城轨列车,算法

Copyright © 2018 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
伴随着我国城市化进程的加快,城市交通压力越来越大,为形成方便快捷的城市交通网络,越来越多的城市将建设城市轨道交通纳入计划。地铁作为城市轨道交通的主力军,其技术性能直接影响运载能力。制动技术作为保障列车运行的关键技术之一,一直备受关注。制动系统是列车操纵系统的组成部分,它用来调节车速和进行停车,是列车安全可靠运行的基础。现代城轨列车常用电空混合制动系统,它通过制动控制器协调电制动和空气制动的介入比例,基本能够保证在车速变化情况下一致的制动性能。
文献 [1] 基于模糊预测控制的方法,根据列车运行过程中几个优化控制目标确定其相应的评价函数,并建立多步预测控制模型,用多目标满意优化模型进行滚动优化。文献 [2] 设计了基于模糊预测控制的城轨列车PID速度控制器,使列车的跟踪性、舒适度等指标都有了明显的改善。文献 [3] 采用模糊预测控制算法,针对列车自动驾驶的性能指标建立对应的模糊隶属度函数,基于人工驾驶策略建立了相应的模糊控制规则,对惰行节能优化进行了曲线优化。文献 [4] [5] 提出的基于模糊预测控制的制动控制方法,利用模糊遗传算法进行滚动优化,获得了全局最优解作为预测控制控制器的输出,进而提高了系统控制快速性和稳定性。文献 [6] 提出了带有舒适度约束条件的模糊预测-PID复合控制方法,分情况进行制动距离的优化。由于制动系统本身存在时滞,会对闭环系统稳定性造成破坏,因此制动系统通常采取开环控制策略。然而,线路阻力的不确定性、闸瓦摩擦系数的非线性及制动系统所受随机扰动都会对制动系统带来不利影响。开环控制方法由于无法消除这些因素的影响,从而在一定程度上降低了制动系统的性能 [7] [8] [9] 。本研究拟对城轨列车制动控制这样一类具有非线性、时变性和迟滞特性的控制对象进行研究,通过分析其动态过程,以及相关因素对控制的影响,提出一种基于T-S模糊预测控制模型的制动控制方法,并进行仿真和优化设计,实现制动控制系统的快速和精确制动。
2. 基于T-S模糊模型的广义预测控制算法
广义预测控制算法(GPC)最初由Clarke和其合作者于1987年提出,在广义最小方差控制的基础上,采用传统的参数模型,引入了不相等的预测水平和控制水平,具有预测模型、滚动优化和反馈校正三个基本特征 [6] [7] [8] [10] 。该算法通过优化中引入的多步预测的思想,对于过程参数慢时变的系统,易于在线估计参数。通过对城轨列车制动系统分析,建立如图1所示的控制系统结构框图。
2.1. T-S模糊模型
作为非线性模型一种的模糊模型,可以方便的表达非线性系统的动态特性,能够任意精度逼近任意
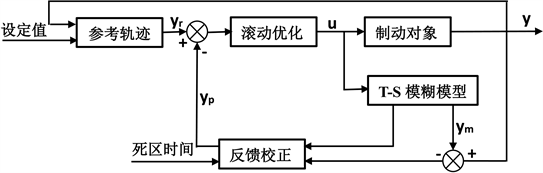
Figure 1. Structure diagram of train predictive control system based on T-S fuzzy model
图1. 基于T-S模糊模型的预测控制系统结构图
非线性系统。T-S模糊模型是由采用规则语句和多项式线性方程组成,规则语句是条件,多项式方程是结论。T-S模型是在表达非线性系统的输出时更优。将模糊变化量作为规则输入,所得结论是线性化结果,模糊建模实现全局线性化,克服了现实控制系统的高维问题,因此T-S模糊模型适合非线性复杂系统建模。多输入单输出T-S模型的可按如下:
(1)
(2)
式中, 表示第i条规则; 表示模糊子集空间; 表示第i条模糊规则输出; 表示结论参数。 为模糊系统的状态向量。 , 。
(3)
其中 ,为第i条规则的激活度。如果将 代入公式(3)可以得到:
(4)
T-S模糊模型的建立主要分为结构辨识和参数辨识。与结构辨识相比,模糊模型的参数辨识要相对容易和成熟的多,主要可以分为两个大类,一类是基于梯度学习与最小二乘法的方法,一类是基于模糊神经网络的学习方法。对于初始的模糊模型,可以采用梯度下降法来调整模糊模型所有前件参数和后件参数,对于前件的输入变量,可以采用三角形,梯形,高斯形等隶属度函数。对于三角形和梯形隶属度函数,由于在其特定的拐点处函数不可微,因此需要加入一定的约束条件,为了避免这种情况,一般采用高斯形隶属度函数。
2.2. T-S模糊预测模型建立及算法分析
T-S模糊模型的预测控制可以进行多步线性化预测控制,对变化相对较慢非线性系统控制效果较好。基于T-S模糊模型的预测控制算法的步骤如下:
1) 首先定义k时刻前提变量对应的模态
,利用近似线性化的系统设计预测控制律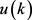 。
。
2) 利用得到的预测控制律 和系统模态 可以得到系统输出 。
3) 根据设计的模糊规则,结合 可以得到新的模型 。
4) 根据新的模型 ,得到 时刻的控制律 ,则可以根据 得到新的 。
在城轨列车的制动控制系统中,可以得到参考序列 ,其各阶段的控制值为恒值,在这里我们把 ,可以使用下列方程求解设定值 。
(5)
其中 。
模糊预测的控制的目的就是使控制对象的输出 尽可能的接近 。本文选取的性能指标函数如下:
(6)
式中,N是最大预测时域,M是控制时域; 是加权控制系数; 是控制加权序列; 是系统第j步的变化量,当 时, 。
假设定义 ,性能指标函数可以简化成:
(7)
可以得到使J取得最小值的控制律为:
(8)
(9)
假设将 矩阵的第一行定义为:
,且
则可以得到基T-S模糊预测模型为:
(10)
式中,
(11)
这样,我们就可以得到制动模糊预测控制模型的控制律为:
(12)
(13)
3. 基于T-S模糊模型的GPC算法仿真分析
基于上述分析,通过在电空制动的列车进行相关的数据采集,利用基于T-S模糊模型的GPC算法对列车的制动控制系统进行仿真,可以得到制动系统的仿真曲线如图2所示。
由图2和图3可知,在制动系统接到制动指令后,模糊预测控制能在最短时间400 ms内达到稳定,制动器的控制压力就可以基本稳定在260 kPa,基本无波动,其制动曲线更接近于目标值,制动更精确;在紧急制动(550 ms)时,模糊预测控制算法比其他算法最先恢复到稳定状态;可知,基于T-S模糊模型的
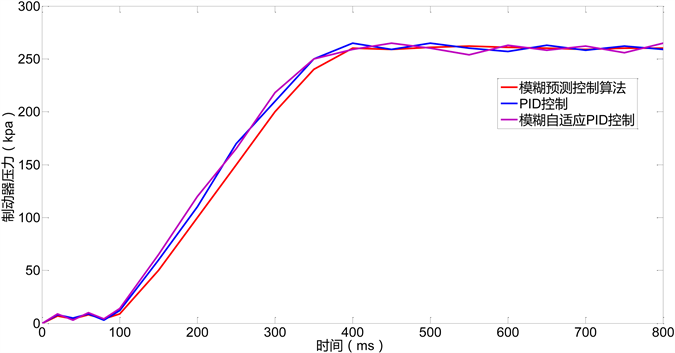
Figure 2. Relationship between brake pressure and time under different algorithms (Normal braking)
图2. 不同算法下制动器压力与时间关系(正常制动)
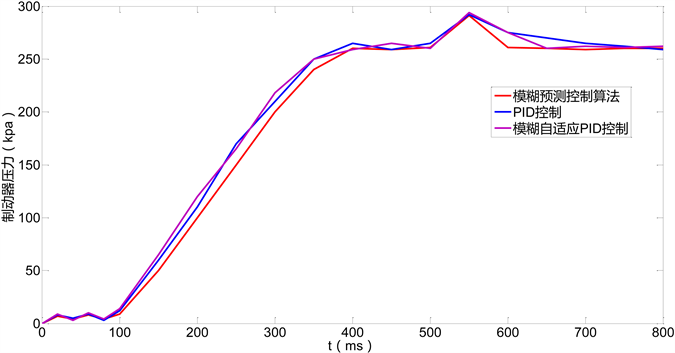
Figure 3. Relationship between brake pressure and time under different algorithms (Emergency braking)
图3. 不同算法下制动器压力与时间关系(紧急制动动)
GPC算法在控制精度上明显优于模糊自适应PID控制和PID 控制。但在上升过程中,100ms之前有一定的波动。经过分析,出现以上问题的原因主要是:(1)列车制动过程中进行的是滚动优化过程,其不同静态实验,会存在的随机性干扰,例如:恶劣的自然环境、实际列车运行过程中车体内的气动总风是变量,实时处于波动状态、制动控制的增量可能会受到预测误差的影响和其他的一些不稳定因素等。(2)列车制动控制系统本身具有很多特性误差。在制动控制中,每当气压上升或者下降达到目标值附近之后就会产生一个逆向的回落过程,这将导致系统收敛缓慢,精度不高,严重的可以直接导致系统无法制动缓解;用于控制制动的高速电空开关阀自身特性时刻也会影响着系统的控制精度;其他随机干扰和建模误差,甚至某些误差通过一般的反馈校正方法也无法有效的进行消除。
4. 结论
城轨列车制动系统受限于地面、环境、天气、人员等影响,具有复杂性、非线性、大迟滞、不确定性等因素,因此精确的数学模型难以获得,本研究提出的模糊预测控制算法则可以充分发挥其优势。根据列车制动的紧急情况进行分类模糊处理,可以实施进行制动力的调整,实施制动力的滚动优化,准确的预测列车下一步的动向。根据仿真结果可知,该算法当需要紧急制动时,压力反馈很难测量,采用模糊预测控制能够更好地避免压力反馈的实时性问题,更好地给出列车的下一步动向。仿真结果表明,该算法在制动力控制方面表现良好,可以在很大程度上减小了非线性因素的影响,同时增强了压力控制的响应可控性。因此,可以提高城轨车辆制动同步性、减小列车纵向力和保证车辆安全运营。
本研究提出的算法通过综合利用实时信息和模型信息,对目标函数不断进行滚动优化,并根据实际测得的对象输出修正或补偿预测模型。因此该算法适用于复杂的工业过程,并在可以在复杂工业过程控制中获得广泛的应用。但是由于原有滚动优化方法和反馈校正方法也会存在无法有效地克服受控对象的不确定性、迟滞和时变等因素的动态影响,从而达到预期的控制目标,并使系统具有良好的鲁棒性和稳定性。因此,需要结合其他智能控制方法,进一步实现列车制动系统制动量的精确、快速、稳定的控制,更好的实现列车的安全运行和提供优质服务。
基金项目
河南省科技攻关项目(172102210124);河南省高等学校青年骨干教师培养计划项目(2016GGJS-287);河南省高校重点科研项目(18B460003)。
文章引用
王晓侃,王 琼. 基于T-S模糊模型的预测控制算法在城轨列车制动控制中的应用
Application of Predictive Control Algorithm Based on T-S Fuzzy Model in Urban Rail Train Braking Control[J]. 计算机科学与应用, 2018, 08(11): 1720-1725. https://doi.org/10.12677/CSA.2018.811190
参考文献
- 1. 刘佳政, 徐娟. 基于模糊预测控制的列车自动驾驶控制算法研究[J]. 控制与信息技术, 2018(1): 7-11, 20.
- 2. 何少雯. 基于模糊预测控制的城轨列车速度控制器研究与仿真[J]. 工业控制计算机, 2017, 30(12): 61-63.
- 3. 何坤, 肖壮, 朱宇清, 毛畅海. 基于模糊预测控制的城轨列车自动驾驶[J]. 现代计算机(专业版), 2017(35): 28-34.
- 4. 戴成龙. 基于模糊预测控制的机车制动控制方法[J]. 现代国企研究, 2017(6): 143.
- 5. 陈洪满, 孙成慧. T-S模糊预测控制地铁车辆制动缸压力控制应用研究[J]. 现代制造技术与装备, 2017(1): 1-3.
- 6. 师黎, 王江涛. 模糊预测-PID复合控制在高速列车制动中的应用[J]. 计算机工程与应用, 2010, 46(31): 228-231.
- 7. Cao, Y., Ma, L. and Zhang, Y. (2018) Application of Fuzzy Predictive Control Technology in Au-tomatic Train Operation. Cluster Computing, No. 1, 1-10. https://doi.org/10.1007/s10586-018-2258-0
- 8. Cheng, L., Liu, W., Hou, Z.G., et al. (2017) An Adaptive Takagi-Sugeno Fuzzy Model Based Predictive Controller for Piezoelectric Actuators. IEEE Transactions on Industrial Electronics, 64, 3048-3058. https://doi.org/10.1109/TIE.2016.2644603
- 9. Zahaf, A., Bououden, S. and Chadli, M. (2017) Constrained Fuzzy Predictive Control Design Based on the PDC Approach. In: Recent Advances in Electrical Engineering and Control Applications, Springer Inter-national Publishing, 140-154.
- 10. Teng, L., Wang, Y., Cai, W., et al. (2017) Robust Model Predictive Control of Discrete Nonlinear Systems with Time Delays and Disturbances via T-S Fuzzy Approach. Journal of Process Control, 53, 70-79. https://doi.org/10.1016/j.jprocont.2016.11.012