Management Science and Engineering
Vol.05 No.04(2016), Article ID:19449,11
pages
10.12677/MSE.2016.54026
A Study of Linear Programming Modeling and Optimization on Operational Production Scheduling for Batch/Continuous Mixed Production in M Company
Yue Zhang
Beijing Lechun Commercial & Trading Co., Ltd., Beijing

Received: Dec. 8th, 2016; accepted: Dec. 27th, 2016; published: Dec. 30th, 2016
Copyright © 2016 by author and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
This article has set up a linear programming model to determine M company’s operational production planning, with an optimal output compared with the current manual scheduling operation. This model has chosen a typical line in the M production, which is a mix of batch and sequential production; it has used the evened weekly production plan as an input, the detailed operational production time/batch of all packaging machine and coating line as an output, and has performed a careful selection on modeling assumptions, target function and constraints. The model has used solver as a key solving tool, and has run an optimized result which would generate a minimum cost for production. On top of this, a correction and discussion on the results are performed based on production needs to better fit into the overall execution. This paper has also proposed a general rule to apply in similar productions, offered suggestions for future optimization, and therefore has great value in future applications in similar enterprises.
Keywords:Operational Production Planning, Linear Programming Model, Mathematical Modeling, Model Optimization

M公司批次/连续混合型生产作业计划中线性 规划模型构建及优化的应用研究
张悦
北京乐纯悠品商贸有限公司,北京

收稿日期:2016年12月8日;录用日期:2016年12月27日;发布日期:2016年12月30日

摘 要
本文结合M公司面临的内外部环境以及目标,选取了代表性的MD生产线,结合其半成品批次生产和包装成品连续生产的特点,建立了一套解决现存人工排产弊端的生产作业计划数学规划模型。模型以进行平衡化处理后的周产品计划作为输入,以各台包装机和关键工艺涂层间的具体作业计划作为输出,对其建模假设、目标函数和约束条件进行了仔细选择,利用线性规划和求解软件工具,实际模拟出了可以取得最小生产费用的优化结果。在此基础上,结合实际生产数据样本进行了结果探讨;并且从生产的实际情况出发,对优化结果进行了探讨和调整优化。最后,论文对类似企业的应用进行了应用前提的提炼,并对应用的进一步优化提出了建议。
关键词 :生产作业计划,线性规划模型,数学建模,模型优化

1. 引言
消费品生产企业与国计民生息息相关,在国民经济中有着举足轻重、不可替代的作用。随着国民日常生活水平的日益提高,外资企业对市场的培育,市场竞争日趋激烈,快速消费品的生产管理不断向纵深发展。特别是近几年来,外部压力不断增大,对于生产计划提出了更高的科学化发展要求。外部压力集中体现在:一、日趋复杂和分散的消费者需求;二、原材料价格上涨,市场和研发成本高居不下,导致对供应链成本降低的要求高;三、销售渠道向纵深化发展,对供应链提出了更高的要求。
然而,要实现准确、快速、灵活的生产计划,在企业当中面临着诸多挑战,主要来源于:一、为了建立竞争壁垒的日趋复杂的多层制作工艺。各工序之间虽有联系,但也相对独立,因此在生产主计划之外,其实还有多层半成品计划的应用需要。二、需求的不确定性;三、成本控制方面的要求,主要体现为库存控制的要求;四、人力安排的困境,加剧了管理者的挑战。如果不能妥当管理,将直接威胁到正常的运营和企业声誉。
快消企业在生产计划管理方面存在上述的挑战,但目前即使是大型跨国企业,也还在分别摸索之中,对于生产主计划乃至作业计划层面可供参考的理论体系和案例不够完善和丰富,对于广大中小企业来说更是其实现精细化管理的一大难题,直接关系到企业的盈利状况和未来发展的程度。
生产计划实践经过了半个多世纪的发展,基本理论和方法以及在各个方面的应用已经日趋成熟。在国内外对生产计划管理的众多研究主要集中在物流配送,现场排产的优化,生产计划仿真等方面。在面向精益生产的生产计划流程与优化模型中,已经有了与企业实践结合较紧密的研究。在计划模型系统中,线性规划模型得到了广泛的应用,涉及的行业包括石油、航空、轻工、机械等多个行业。从单产品计划优化的目标模型,以及多产品并行建造计划综合优化目标模型,已经在建模和算法上由了比较成熟的研究 [1] 。同时,也开始出现了结合离散随机需求的实际情况进行算法推演,以及实际算例验证的生产计划优化研究 [2] 。多厂生产计划模型实现了原来供应与产品限量平均分配、原料优化分配多厂模型、原料和产品分别优化分配的多厂模型等应用,进行实际排产 [3] ,并进行了多厂模型系统经济效益比较,使用后可以比单厂模型系统优化取得更大的经济效益,并且能够根据市场变化迅速调整公司计划,使企业可以实现快速反应与效益最大化的最佳平衡。对于小批量多品种的加工厂,线性规划也可以创造价值,然而在“均衡生产”的实现当中,依然需要依靠经验来实现。
20年代50年代后期,学术界涌现出了很多新的算法,不断完善对线性规划模型的研究。例如,1954年提出的对偶单纯形法,参数规划问题和灵敏度分析,1956年提出的互补松弛定理,以及之后的分解算法等。在生产计划和调度当中,实际用来解决生产计划问题的包括经典数学规划法、基于规则的方法、排序法、基于DEDS的解析模型方法、智能搜索算法(包括模拟退火算法、蚁群算法、遗传算法 [4] 、免疫算法 [5] 、禁忌搜索法)以及基于智能的调度方法等 [6] 。在实际的工业计划和调度问题当中,经典的间歇性生产规划问题主要采用分支定界和启发式调度解法。分支定界法通常会产生大量的整数变量,在实际的建模和求解过程当中都会花费大量的时间,因而不适合解决大规模的生产计划问题 [7] ;而启发式调度法虽然可以避免过量的计算,但利用次优解代替最优解的同时,对于突发事件和不确定性变化的处理依然有限 [8] 。近些年来,模仿生物界规律的蚁群优化算法开始得到更多的追捧,自推出以来在理论研究和实践应用上也得到了诸多发展 [9] 。在生产计划当中,为了应对环境的不确定性,也出现了对于综合性生产模型的探讨,特别面向产能柔性的企业。这些研究对整体成本最小化的建模以及遗产算法的求解,通过实例仿真,对模型和算法的有效性、以及可行性进行了验证 [10] 。列生成技术也在总拖期生产计划问题当中与数学模型相结合,通过将变量当中对目标函数影响较大的基本参数与非基本参数进行区分,可以解决诸如硬盘生产中如何排布,并为谁生产这样的较大规模变量的建构类排产问题 [11] ,并且为滚动性排产和工间的整数型限制留出了未来的发展空间。
在现有的学术研究当中,对于算法的讨论常常是研究的重点,但这些研究本身的建模需要花费大量的精力,难以在应用当中产生足够简便的应用价值。在实际学术研究中,这些应用不能快速复制到企业实际生产的动态数据当中,也很少涉及在运行过程中的主要成功因素和阻力的探讨实践。这些都是本文研究的重点和难点。在企业应用当中,将消费终端订单或市场需求预测转化为生产计划,已经有了较成熟的经验,对于间歇生产作业计划、连续生产作业计划、批量计算都有了不少相应的研究,但是仍然缺乏一种工具能够将实际经验与理论工具完美结合,将生产主计划转换为多层作业计划,特别是在批次/混合型的生产过程中,目前还缺乏充分的理论依据和操作方法。
根据在企业的工作经验,生产计划管理中运用数学规划得当,具有重要的现实意义:一、提高客户服务水平,提高产品新鲜度;二、降低库存,节省现金,提高利润率;三、通过系统性解决排产问题,减少内部管理成本;四、建立更加灵活的供应链,维持和创建竞争优势。这些方面的探索,都可以为其他类似企业的管理者提供生产计划管理方法和思路的借鉴依据。
2. MD生产线的现状分析
M公司全球销售量最大的MD生产线,是批次半成品和连续包装线相混合生产线的一个典型代表。MD生产线的基本工艺流程见图1。
在整个生产线中,涂层工艺由于设备价值高、工艺时间长,被认定是整个MD生产线当中的核心生产环节,但在实际排产过程当中,由于代表市场的需求端更加关心最终成品的交付,从需求预测,到长期计划,到生产计划,都是以最终包装成品为单位下达。这样,构成/形成了批次半成品和连续包装生产线的组合。生产线计划的编制和下达过程如图2所示。
从流程当中可以看出,包装的最终成品计划与生产线的“瓶颈环节”——涂层制作之间存在脱节。在实际操作过程中,短期计划会同时下达至涂层制作和包装工位,但是只有包装工位的成品计划是准确的,涂层制作的计划通常只能以整周下达,其每日生产计划相对只是一个参考。这一差距是由生产线每
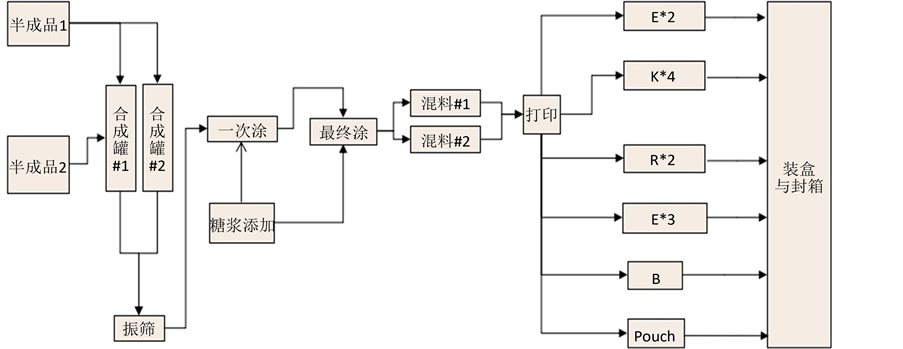
Figure 1. Basic process flow of MD production line
图1. MD生产线的基本工艺流程
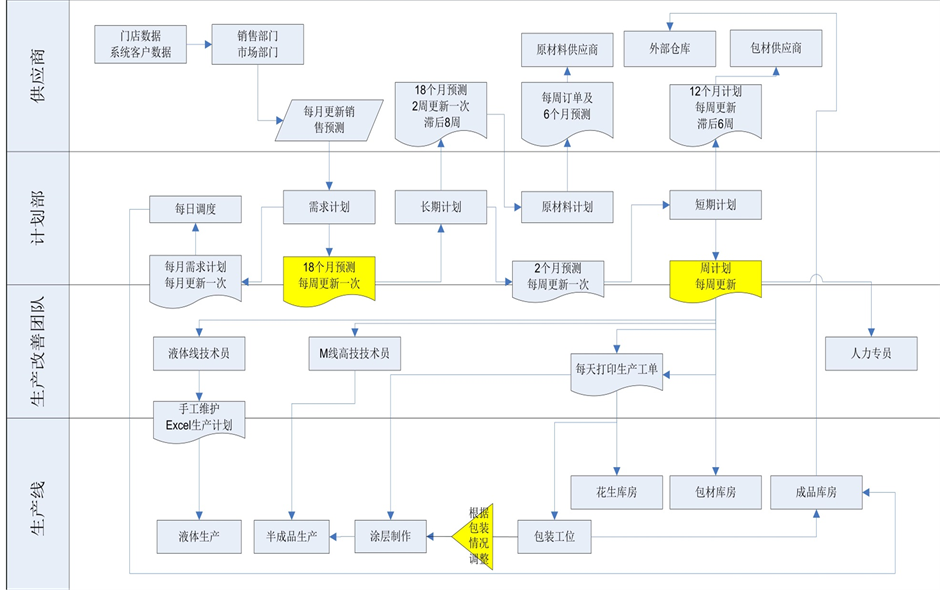
Figure 2. Production planning process of MD production line
图2. MD生产线的生产计划流程
日的实时调整进行弥补的。
这样的调整,有些类似于不同工位之间的“拉动式”生产,这样的半成品排产模式生产模式在效率、灵活方面有一些明显的好处,但是这样的由生产线进行调配的排产也存在其主要的弊端:首先,班组分散排产,缺乏统筹规划,有可能造成当班半成品生产过量,或未给下一班遗留够产量,降低效率,增加人力和各项相关生产成本;同时,对于以瓶颈环节定义的“整线生产效率”指标,由于半成品排产的主动权掌握在班组手中,而难以反应真实水平,使生产线缺乏动力进行产量提升和换产减少的相关改善。
在人工排产能力受限的时候,应该借助科学管理的工具来帮助进行优化配置。根据建模的目标和各种数量模型的特点,我们选取了运用较为广泛的线性规划来进行建模研究。选取该方法的原因主要是:一、该问题主要是在一定约束条件(排产的规则)内,寻求整体效率最大化,或费用最小化的规划求解问题,而主要变量(排产时间)与最终费用直接可以体现为一般线性关系,符合线性规划的基本建模条件;二、线性规划求解的原理相对简单,并且可以由Excel、Lingo等广泛使用的软件支持求解,便于企业应用和试错,可以迅速取得结果,验证效益。
3. M公司生产作业计划优化的必要性和可行性
3.1. 生产作业计划优化的必要性
分析M公司的外部环境,一方面国家对于不会耗费大量稀缺资源,且无严重环境污染的快速消费品(尤其是食品生产),并没有相应的调控政策予以限制;另一方面,国家一些相关政策客观上也在影响着M公司的运营,例如对于食品安全的日趋重视,对外资企业逐渐取消“超国民待遇”,国家反腐的政策措施对奢侈品送礼消费的客观限制,使行业面临越来越多的挑战,但对于真正修炼内功的企业来说,也是进一步增大市场份额的机遇。
从M公司面临的行业内竞争来看,形势较为严峻。供求关系已经转变为供大于求,竞争者越来越多,各个品牌开始逐渐采用差异化营销。M公司作为外资公司中的市场先入者,原有的市场认知优势被逐渐削弱,近两年,随着F公司、H公司以及欧洲、日本许多强大竞争对手的加入,国有企业J公司及许多本土小公司的生存空间被挤压。M公司与外资厂商的竞争更加直接和剧烈,并且贯穿从终端销售到工厂运营的供应链各个方面。
M公司为适应外部环境和应对竞争,在保证食品安全的前提下,供应链必须更加“精简、灵活、可持续”,在运营和服务上全面做深做细,进一步提高竞争能力。对于生产计划,则要求其更灵活、更高效、更接近市场和有利于创建合作关系,并且保持和增强其多品种批量生产的低成本。
从内部分析,M公司的生产成本有逐年上升的趋势,保持之前的盈利水平变得越来越难。另一方面,M公司的增长开始出现拐点,使得成本控制的压力更为加大。
目前,M公司大部分生产线的生产计划虽然可以实现对于终产品计划以小时为单位下达,但是实际的生产订单完成率的衡量单位是一周,即只要在当周按照订单规定的产品种类和数量完成计划,即视为订单得到满足。至于具体的生产作业计划,特别是半成品生产计划可以说只是一个参考值,班组的实际作业计划无法得到精确的记录,只有一些当班生产完成之后的结算结果,这些结果也被分散记录在Excel表内,无法得到统一的收集整理,至于在有限因素下实行科学的最优化更是无从谈起。
作业计划对成本控制的考虑,除了要解决生产成本和库存成本等物流成本的综合最小费用问题外——如果单班排产量过小,会增加生产成本;反之,则可能会造成库存过大,增加库存成本等物流成本。
在M公司生产成本中,人力成本占很大比重且居高不下。这是生产计划工作面临的一个重大挑战。与此相关的另外一大问题是其突出的季节性。在全年最旺和最淡的季节,其销售比可达5:1,淡旺季对于人力的需求最大可能相差500~600人。这样,使得生产计划要有效控制人工成本较为困难。
在计划部门组织结构方面,M公司的生产计划部门,对内对外,需要直接与许多公司内部其他部门和外部多家供应商直接进行接触,存在大量多向沟通和文件维护,负责主持供应分析会议、中期计划会议等多个重要会议。制定计划及进行计划调整,保证计划的合理性和高效性实属不易。然而,工厂计划部门一共只有5人,计划人员能力也有待提高,其大量时间花费在系统的基本维护、内外沟通和反应调整当中,很难有精力进行生产多层计划的深挖,或是系统性的优化。
在技术支持方面,M公司的生产计划主要依赖一种ERP软件进行生产计划。但是这套软件系统目前对外无法与供应商的系统进行对接,对内无法与生产一线的操作系统实时对接,对整个生产线的信息响应严重滞后。因此在公司内部,有三天之内计划不得随意变更的规则,在实际当中,却存在一个月10次以上的违反,造成了大量的重复工作。在淡季需要跨班进行加班人员支持的情况下,这些计划的临时变更无疑大大增加了管理成本、出错的可能,和由于怕麻烦而丧失掉最佳人力配置的机会。
因此,计划工作的优化包括计划方法的改进势在必行。
3.2. 生产作业计划建模优化的可行性
此次建模的目的,主要是希望能够将M公司MD生产线月生产主计划,转化成为可执行的包装以及半成品生产计划,便于一线执行,并能够在满足生产限制条件的前提下,尽量实现成本最小化。
关于数据的可得性,在建模过程中,需要了解一些生产执行的限制因素、生产线运行的标准产量、排产相关的费用信息、和生产计划的基础数据。当数据分散难以整理时,可以以其中几周的数据综合进行模拟,取得一个平准化的产量信息。
由基层发起的数据建模优化,需要企业具备相对完善、成熟的电子信息系统,以便及时收集、处理数据;但又要求系统有一定灵活性,使得新建模型可以与现有系统顺利对接。M公司有比较完善的企业内部局域网,已经上线6年的SAP系统运转有效。然而,计划流程还保留了不少手工操作,如日生产计划的下达、半成品生产计划的核对、当日产量记录的原始数据抓取等,还是采取手工操作方式,为计划工作的优化留出了一些空间。
在实施的可行性上,在管理层支持方面,M公司一向非常重视基层的创新活动。这些改善型举措也同时来自于组织结构调整、业务流程改善和技术改造等各个层面。与之相互呼应的是,公司十分重视人才的引进与培养,并通过提供具有竞争力的薪酬吸引到不少专业人才。这在客观上,为生产作业计划开展建模优化提供了良好基础。
4. M公司生产作业计划规划模型
4.1. 建模的基本内容和假设
经过前期的基本研究,M产品生产线半成品作业计划内容可以简化为以下描述:根据长期计划中的包装成品需要,结合半成品生产线和包装机的生产能力,获得包装成品和涂层制作半成品生产线的最优生产计划排产。建模所需的参数说明见表1。
为了顺利进行建模工作,对模型实现的前提做一些假设:1) 主生产计划的时间跨度为周。2) 建模的频率为每月一次。3) 包装机标准班产进行同一包装种类的合并。4) 包装机及包装组合以实际匹配为准,不考虑建模过程和实验过程中产生的新组合和变化。根据系统中的数据和机器组合,得出标准班产矩阵如表2。
从中可以看出,实际的产品/包装机组合有9种。
4.2. 建模的目标
生产作业计划的目标通常有两个大的方向,一是生产线利用率的最大化,一是生产线费用的最小化。由于近几年产能扩张已经完全能够满足市场需求,目前的生产作业计划,正在从生产线利用率的最大化,逐步向生产费用的最小化进行转移(淡季时尤其如此)。我们将与生产开班直接相关的人工、能源、易耗品部分组成的总生产费用(与排产相关的可变成本)最小,作为作业计划的决策目标。
2014年实际每单位班组生产费用的可变费用如表3。
4.3. 决策变量和约束条件
由于需要平衡包装线与生产作业计划,在此将一周的计划作为已知变量,将每台包装机每种产品的
Table 1. List of arguments
表1. 参数说明列表
Table 2. MD production line packaging machine standard class
表2. MD生产线包装机标准班产矩阵
Table 3. MD production line of each process area variable cost per shift
表3. MD生产线各工艺区域每班组可变成本
注:由于成本信息属于商业机密,此数字经过了数倍缩小化处理,相对关系不变。
运行时间(连续型生产)以及半成品线的批次计划(批次型生产)作为决策变量。
因为包装机的计划对应班产,其决策变量应为每班内运行时间,这一时间在每台包装机的加总应该是非负且小于1的一个数(最多开一个班)。而对于半成品线,其批次性生产决策变量应为小于等于5(最大生产批次)的整数批次;最佳的生产计划是严格按照订单生产,也就是说,既不能多也不能少,这样可以最大程度地减少库存成本和减少损失销售;同时,还需要考虑到半成品的遗留和物料平衡。
综上,建立模型如下:
在每个班次j内,根据物料平衡,涂层半成品产量大于等于包装产量,式(2);每台包装机生产班数≤1,式(3);涂层生产批次≤5,式(4);每种产品满足当周订单,式(5);每班的物料平衡,式(6);非负性约束,式(7):
 (1)
(1)
满足约束:
 (2)
(2)
 (3.1)
(3.1)
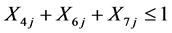 (3.2)
(3.2)
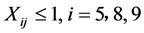 (3.3)
(3.3)
 (4)
(4)
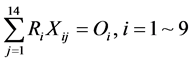 (5)
(5)
 (6)
(6)
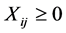 (7)
(7)
4.4. 应用软件对生产作业计划建模
将各种包装产品组合和涂层间计划以矩阵形式表示,每行的总班数为前面一周开班数的汇总,总产量为班数与每班标准产出的乘积。最终应得出每种产品与当周的成品计划相等。其中,当期的成品与半成品差距成为期末库存,而本期成品需求减去上期库存,则为当期半成品需求。之后,将包装机计划进行汇总(将同样设备的生产计划进行加总),以便添加每台设备的限制条件(单台设备每班开班数最多为1),和计算总成本。其中,此处将每种设备的总开班数与设备的单班成本分别相乘,其加总结果即为总成本。显然,将包装机与涂层成本加总后,即为生产总成本。接下来,打开软件规划求解模块,在对话框当中分别对目标单元格、可变单元格、约束条件进行定义。
4.5. 以样本数据进行原始求解
为了对模型进行初步检验,我们选取了在淡旺季转换期间7月份的数据进行均衡化之后,对模型进行规划求解。可变参数Oi根据每段实际生产目标确定,见表4。
经过线性规划求解后,得出以下结果如图3。
其中,黄色单元格是决策的开班组合,蓝色是固定参数,橙色是组合出最小化的总费用。从结果可以看出,包装区域的总可变费用为35,564,涂层区域的总费用10,793,总费用为46,357。
5. 运行结果分析
通过将模型运行的结果与去年该生产线同期费用的比对,以及与6月份另外一条批次/连续混合生产线的比较,相对于现行排产规则的总费用(5万以上),总费用实现了7%左右的节省,是一个相当不错的结果。
对于整体生产线的瓶颈——涂层间来说,开班率为100%,批次利用率61.4%。而对几台包装机的利用,也符合生产实际,可见模型规划的结果,在实现对包装产量支持的同时,基本实现了对设备的最大化利用。
Table 4. Variable parameter Oi
表4. 可变参数Oi

Figure 3. The original solution of the mathematical model
图3. 数学模型原始求解结果
虽然整个设备的利用率看来趋于合理,但是实际上包装机都出现了一些“断续”的开班和换产,在实际操作当中造成了一些困难。例如,B包装机4.2个班的生产任务,却断断续续开了8个班。对于这个问题,最好的解决方式是将换产次数统计后直接折算成相应的成本,加入进整体成本当中。但是,目前由于建模的复杂性所限,换产的成本尚未折算进整体的成本计算当中。但可以引入一个向上取整的“开班数”计数函数,将其做一个最小化的考量。
与上面提到的问题类似,目前的产品生产安排建模当中,很多都突破了现行的“最小订单”的限制,有的包装机甚至出现了0.02个班的生产(实际生产只有12分钟)。解决这一问题的最好办法是为每一个订单设定最小生产量的限制,即“为0,或者是在最小生产量到1之间”。目前在规划求解软件初级版当中暂时无法实现这一逻辑设置,最简便的方法就是进行一些合并调整,取得次优解。
其实,由于此线性规划的最优解不唯一,通过多次求解,可以在目标值不变的情况下,比较几个最优解,得出一个相对更易于操作的解,例如下图4。

Figure 4. Mathematical model two solving results
图4. 数学模型二次求解结果
从上图显示的这个解,在总生产费用保持46,357不变的情况下,B机的开机班数从原来的断续8个班次,减少为5个班次,大大减小了操作的复杂性和不必要的浪费。类似的,也可以结合企业和生产线的实际情况,对其他机器的运行指数进行评价。
从模型本身看来,涉及70,000多次的运算,对于一些基本设备来看,运算速度相对较慢。为了进一步提高模型求解速度,还可以对模型本身进行优化,包括减少不必要的约束条件,将相等性限制条件改为开放性限制条件,保持线性求解,降低精度等。
综合看来,这套模型求解的结论,具有一定的实际借鉴意义。但由于模型本身的设计所限,还有一些不尽如人意之处。这些不足,有些可以通过建模优化进行解决,有些暂时还没有好的解决方案,可以考虑在软件计算得出最优解之后,进行智能调整处理,得出一个次优解,从而最大程度地在保留其最优设计的同时,能够在生产实际当中得以顺利实施。
这次数学模型的构建启发我们,在生产计划模型构建过程中,不但需要生产视角,还需要生产计划的视角,甚至面向整个供应链,而不是面向单一的部门。同时,在模型构建当中,需要及时考虑到可能出现的问题和阻力,并且在模型构建当中尽可能予以考虑和解决。在这个过程当中,需要进行不同的关键人物访谈,换位思考也很重要。在数学模型的构建中,也需要采取创新思维,比如进行相似订单的合并,加入二级评价指数,以及在模型无法实现的情况下进行智能调整等。在线性规划模型的使用中,体会到“最优解”不是万能的,数学模型有时候只能得到局部最优解,而需要多次的运行和调整才能找到“系统最优”,这当中不但需要智慧,更需要耐心。希望今后继续类似的实践,使生产作业计划中数学模型的应用更加深入,更为有效。
文章引用
张悦. M公司批次/连续混合型生产作业计划中线性规划模型构建及优化的应用研究
A Study of Linear Programming Modeling and Optimization on Operational Production Scheduling for Batch/Continuous Mixed Production in M Company[J]. 管理科学与工程, 2016, 05(04): 237-247. http://dx.doi.org/10.12677/MSE.2016.54026
参考文献 (References)
- 1. 宗鸣镝, 孙厚芳. 面向精益生产的造船生产计划流程与优化模型[J]. 辽宁工程技术大学学报(自然科学版), 2011(2): 120-125.
- 2. 宁晓峰, 史峰, 徐光明. 离散随机需求下共用装配线生产计划优化[J]. 计算机集成制造系统, 2014(4): 847-853.
- 3. 于小桥, 杨明诗, 等. 多厂生产计划模型系统[J]. 石油炼制与化工, 2002, 33(1): 50-53.
- 4. 沈爱莲. 基于遗传算法的流水车间调度的方法及实际应用[D]: [硕士学位论文]. 杭州: 浙江工业大学, 2007.
- 5. 苏生, 等. 基于免疫算法的并行机间歇过程模糊生产调度[J]. 计算机集成制造系统, 2006, 12(8): 1252-1257.
- 6. Palmer, D.S. (1965) Sequencing Jobs through a Multi-Stage Process in the Minimum Total Time: A Quick Method of Obtaining a Near Optimum. Operational Research Quarterly, 16, 101-107. https://doi.org/10.1057/jors.1965.8
- 7. Wu, D. (2003) Decomposition Approaches for the Efficient Solutions of Short Term Scheduling Problems. Computers and Chemical Engineering, 27, 1261-1276. https://doi.org/10.1016/S0098-1354(03)00051-6
- 8. 王万良, 等. 生产调度智能算法及其应用[M]. 北京: 科学出版社, 2007.
- 9. Dorigo, M. (2004) Ant colony optimization. MIT Press, Cambridge, Massachusetts, London.
- 10. 肖佩, 贾国丽, 辜志强. 面向产能柔性的综合生产计划模型研究[J]. 机械工程与自动化, 2007(6): 79-84.
- 11. Lee, L.H., Chew, E.P. and Ng, T.S. (2005) Production Planning with Approved Vendor Matrices for a Hard-Disk Drive Manufacturer. European Journal of Operational Research, 162, 310-324. https://doi.org/10.1016/j.ejor.2003.09.012
