Statistics and Application
Vol.06 No.01(2017), Article ID:20020,6
pages
10.12677/SA.2017.61011
SEE Variable Selection for Joint Mean and Variance Models
Ting Yao, Fengting Lu, Ruiqin Tian, Qiaoqiao Lv
Department of Statistics, Zhejiang Agricultural and Forestry University, Hangzhou Zhejiang

Received: Mar. 9th, 2017; accepted: Mar. 26th, 2017; published: Mar. 29th, 2017

ABSTRACT
The method based on modeling the variance is one of the most commonly used methods to deal with heteroscedasticity. In this paper, we propose a variable selection procedure based on the smooth threshold estimating equations for joint mean and variance models. The proposed variable selection method can select variables and estimate coefficients simultaneously, and does not need to solve convex optimization problem so as to largely reduce computation quantity in practice. Finally, we make some simulations to show that the proposed procedure works satisfactorily.
Keywords:Joint Mean and Variance Models, Heteroscedasticity, Estimating Equation, Variable Selection
均值方差联合模型的SEE变量选择
姚婷,陆凤婷,田瑞琴,吕巧巧
浙江农林大学统计系,浙江 杭州
收稿日期:2017年3月9日;录用日期:2017年3月26日;发布日期:2017年3月29日

摘 要
对方差建立回归模型分析是处理异方差问题中最常用的方法之一。本文基于均值方差联合模型,结合光滑阈估计方程(Smooth Threshold Estimating Equation,简记SEE)方法研究该模型的变量选择方法。该变量选择方法可以同时进行参数估计和变量选择,并且不需要解任何凸优化问题,因此实际应用中将大大减少计算量。最后, 通过随机模拟实验验证了所提出方法的有效性与可行性。
关键词 :均值方差联合模型,异方差,估计方程,变量选择

Copyright © 2017 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
目前由于大部分学者已经意识到了解回归模型中方差的来源以及对方差进行调控的重要性,因此,对方差建立回归模型,即基于均值方差联合模型进行统计推断是处理异方差问题最常用的方法之一。到目前为止,很多作者已经深入讨论了异方差情况下均值方差联合模型的估计、检验和变量选择等统计推断问题。Aitkin [1] 给出了联合均值与方差模型的极大似然估计结果;Verbyla [2] 在提出联合模型限制极大似然估计的同时,更进一步的讨论了该模型的异常值诊断问题;Taylor和Verbyla [3] 则研究了利用t分布的联合位置与尺度来解决含异常值的联合模型检验问题;吴刘仓等 [4] 则在 Box-Cox变换下得出了联合均值与方差模型的参数估计结果。其中关于均值方差联合模型的变量选择的成果有,吴刘仓等 [5] 曾运用SCAD、LASSO等惩罚函数,考虑通过对似然函数进行惩罚以解决该联合模型的变量选择问题,并且证明了该变量选择方法具有相合性和Oracle性质。然而该方法须涉及凸优化问题,且必须在人为地设定一个门限值后才可利用局部二次逼近给出的迭代式得到回归结果,否则就达不到变量选择的目的。由此可见,该变量选择方法的实用性和可操作性并不强。
因此,为解决以上变量选择方法所存在的不足,本文利用Ueki [6] 的基本思想,提出基于光滑阈估计方程的均值与方差联合模型的变量选择新方法,并称之为SEE变量选择方法。该变量选择方法不仅不涉及任何凸优化问题,且可将模型中不重要变量的回归系数以较快速度向零压缩,并最终将其从模型中剔除。随机模拟结果表明该变量选择方法正确有效,且效果及可操作性均较之前方法有明显的改善。
本文的组织结构安排如下:在第2节中,我们首先介绍了均值方差联合模型,并在此基础上提出了该模型基于光滑阈估计方程的变量选择方法以及与此相关的参数调整方法。第3节给出了利用基于局部二次逼近的Gauss-Newton迭代算法来求解光滑阈估计方程的具体步骤。第4节考虑通过模拟研究来验证本文所提出的变量选择方法的可行性。最后在第5节中将给出最终的总结。
2. 基于光滑阈估计方程的变量选择
2.1. 均值方差联合模型
考虑如下正态分布下均值方差联合模型:
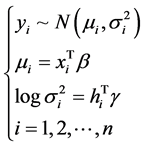 (1)
(1)
其中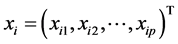 和
和 分别为均值模型及方差模型中的解释变量(由于可能存在同时影响均值及方差的变量,因此对于
分别为均值模型及方差模型中的解释变量(由于可能存在同时影响均值及方差的变量,因此对于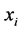 和
和 而言可完全相同、部分相同或完全不相同),
而言可完全相同、部分相同或完全不相同), 和
和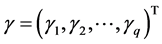 是对应的均值模型及方差模型中的未知参数向量,
是对应的均值模型及方差模型中的未知参数向量, 则是模型的被解释变量。另外,令
则是模型的被解释变量。另外,令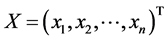 和
和 为解释变量矩阵。
为解释变量矩阵。
2.2. 光滑阈估计方程
根据模型(1),同时在略去与参数无关的常数项后,我们最终可将均值方差联合模型的对数似然函数写为:
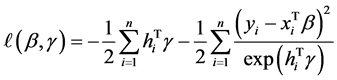 (2)
(2)
则该均值方差联合模型的估计方程为:
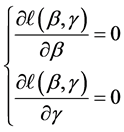 (3)
(3)
据此,我们便可基于Ueki [6] 的思想,改写该模型的估计方程(3),并定义如下均值方差联合模型的光滑阈估计方程:
 (4)
(4)
其中, 和
和 分别为
分别为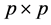 和
和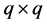 的对角阵;
的对角阵;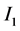 和
和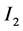 则分别为p阶和q阶单位阵。
则分别为p阶和q阶单位阵。
在这里,考虑到求解(4)式时须对参数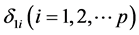 和
和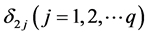 进行设定,因此我们建议参照Ueki [6] 的思想将
进行设定,因此我们建议参照Ueki [6] 的思想将 和
和 取为:
取为:
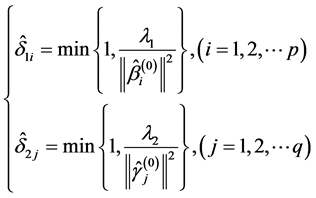 (5)
(5)
其中,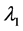 和
和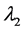 分别为均值部分及方差部分光滑阈估计方程的调整参数,
分别为均值部分及方差部分光滑阈估计方程的调整参数,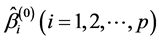 和
和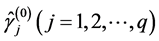 则是
则是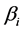 和
和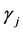 的初始估计,可根据上述(3)式得到。
的初始估计,可根据上述(3)式得到。
另外可以发现,在求解(4)式时,若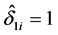 (或
(或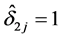 ),则可得
),则可得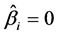 (或
(或 ),表示相应的变量在模型中并无较大意义,可将其剔除,以达到变量选择的目的。因此,从理论来看所提出的光滑阈估计方程可以起到对均值方差联合模型的变量选择的作用。而在第4节中,我们将进一步给出该变量选择方法的实际模拟研究效果。
),表示相应的变量在模型中并无较大意义,可将其剔除,以达到变量选择的目的。因此,从理论来看所提出的光滑阈估计方程可以起到对均值方差联合模型的变量选择的作用。而在第4节中,我们将进一步给出该变量选择方法的实际模拟研究效果。
2.3. 调整参数的选择
对于调整参数 和
和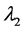 的选取,可以考虑利用交叉核实(CV) [7] ,广义交叉核实(GCV),AIC准则以及BIC准则 [8] 等一些经典的数据驱动准则来进行选取。在这里,我们主要采用BIC准则来确定光滑阈估计方程中的调整参数,并且验证了该方法的可行性。记
的选取,可以考虑利用交叉核实(CV) [7] ,广义交叉核实(GCV),AIC准则以及BIC准则 [8] 等一些经典的数据驱动准则来进行选取。在这里,我们主要采用BIC准则来确定光滑阈估计方程中的调整参数,并且验证了该方法的可行性。记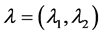 ,其定义如下:
,其定义如下:
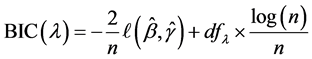 (6)
(6)
其中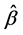 和
和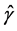 为基于光滑阈估计方程(4)式获得的估计值,
为基于光滑阈估计方程(4)式获得的估计值,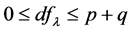 为
为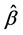 和
和 中非零分量的个数。调整参数可以通过下式获得
中非零分量的个数。调整参数可以通过下式获得
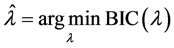 .
.
从第4节的模拟研究结果可以看出,上述调整参数的选择方法是行之有效的。
3. 迭代计算
以下将给出基于Gauss-Newton迭代算法来求解光滑阈估计方程的具体过程。为方便起见,简记上述光滑阈估计方程(4)为:
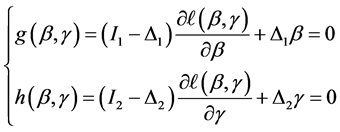 (7)
(7)
以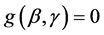 的求解为例,由于注意到对数似然函数
的求解为例,由于注意到对数似然函数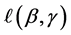 具有连续的一、二阶导函数,因此我们考虑将
具有连续的一、二阶导函数,因此我们考虑将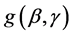 在
在 处进行Taylor展开,得到:
处进行Taylor展开,得到:
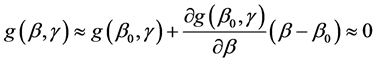 (8)
(8)
通过进一步化简(8)式,并将(7)式结果带入,即可得:
 (9)
(9)
考虑对于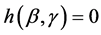 的求解进行如上相同处理,我们最终可得光滑阈估计方程的迭代求解式为:
的求解进行如上相同处理,我们最终可得光滑阈估计方程的迭代求解式为:
 (10)
(10)
其中, 和
和 为迭代初值(第一次迭代初值可取作原始估计方程(3)的解)。尝试重复进行(10)式的迭代计算,直至估计结果收敛,我们便可最终得到光滑阈估计方程的解。
为迭代初值(第一次迭代初值可取作原始估计方程(3)的解)。尝试重复进行(10)式的迭代计算,直至估计结果收敛,我们便可最终得到光滑阈估计方程的解。
4. 模拟研究
在这一节将运用模拟数据来验证本文所提出的利用光滑阈估计方程来解决均值方差联合模型的变量选择问题的可行性。同时,考虑以广义均方误差(GMSE)为精度衡量指标,来将基于光滑阈估计方程的联合模型变量选择效果与基于SCAD、LASSO惩罚函数来进行联合模型的变量选择效果进行比较。利用广义均方误差(GMSE)评价均值方差联合模型中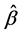 和
和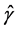 的估计精度,定义如下:
的估计精度,定义如下:
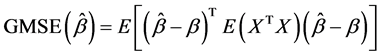 (11)
(11)
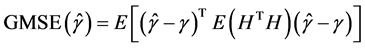 (12)
(12)
为实施模拟研究,我们考虑从模型(1)中产生随机模拟数据。其中,取真值 ,
, ,
,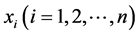 和
和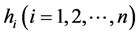 分别独立地产生于
分别独立地产生于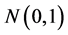 。基于1000次重复试验,表1给出了在样本量分别为100,150以及200的情况下,均值方差联合模型基于光滑阈估计方程(SEE)、SCAD罚函数以及LASSO罚函数的变量选择的平均效果。表1中“C”表示把真实零系数正确估计成0的平均个数;“IC”表示把真实非零系数错误估计成0的平均个数。
。基于1000次重复试验,表1给出了在样本量分别为100,150以及200的情况下,均值方差联合模型基于光滑阈估计方程(SEE)、SCAD罚函数以及LASSO罚函数的变量选择的平均效果。表1中“C”表示把真实零系数正确估计成0的平均个数;“IC”表示把真实非零系数错误估计成0的平均个数。
我们通过表1结果可以得到如下结论:
1) 对于固定的变量选择模型,SEE、SCAD以及LASSO三种方法均各自表现出随着样本量的增大,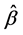 和
和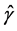 的广义均方误差(GMSE)均越来越小,表示参数估计的精度越来越高。
的广义均方误差(GMSE)均越来越小,表示参数估计的精度越来越高。
2) 在固定的样本量n下,对于基于光滑阈估计方程的变量选择方法(SEE)而言,无论是从均值模型来看,还是从方差模型来看,其参数估计效果均要明显优于基于SCAD或是LASSO惩罚函数的变量选择方法。这表明本论文所提出的基于光滑阈估计方程的均值方差联合模型的变量选择方法是切实可行的。
3) 在固定的变量选择模型和固定的样本量n下,均值模型的变量选择效果均要优于方差模型的变量选择效果。
5. 结论
本文针对基于正态分布的均值方差联合模型,提出了一种利用光滑阈估计方程的变量选择方法。该变量选择方法不仅不涉及任何凸优化问题,且可将模型中不重要变量的回归系数以较快速度向零压缩,并最终将其从模型中剔除。随机模拟结果表明该变量选择方法正确有效,且效果及可操作性均较之前的变量选择方法有明显的改善。
Table 1. The results of variable selection for joint mean and variance models based on different methods.
表1. 基于不同方法,均值方差联合模型的变量选择结果
基金项目
浙江省自然科学基金(LQ15A010008);全国统计科学研究项目(2016LZ06);浙江农林大学创新创业训练计划项目(110-2013200017)。
文章引用
姚婷,陆凤婷,田瑞琴,吕巧巧. 均值方差联合模型的SEE变量选择
SEE Variable Selection for Joint Mean and Variance Models[J]. 统计学与应用, 2017, 06(01): 98-103. http://dx.doi.org/10.12677/SA.2017.61011
参考文献 (References)
- 1. Aitkin, M. (1987) Modelling Variance Heterogeneity in Normal Regression Using GLIM. Applied Statistics, 36, 332- 339.
- 2. Verbyla, A.P. (1993) Modelling Variance Heterogeneity: Residual Maximum Likelihood and Diagnostics. Journal of the Royal Statistical Society: Series B, 52, 493-508.
- 3. Taylor, J.T. and Verbyla, A.P. (2004) Joint Modelling of Location and Scale Parameters of the t Distribution. Statisti- cal Modelling, 4, 91-112.
- 4. 吴刘仓, 黄丽, 戴琳. Box-Cox变换下联合均值与方差模型的极大似然估计[J]. 统计与信息论坛, 2012, 27(5): 3-8.
- 5. 吴刘仓, 张忠占, 徐登可. 联合均值与方差模型的变量选择[J]. 系统工程理论与实践, 2012, 32(8): 1754-1759.
- 6. Ueki, M. (2009) A Note on Automatic Variable Selection Using Smooth-Threshold Estimating Equations. Biometrika, 96, 1005-1011.
- 7. 赵培信. 基于光滑门限估计方程的变系数EV模型的变量选择方法[J]. 重庆工商大学学报(自然科学版), 2013, 30(9): 1-5.
- 8. Wang, H., Li, R. and Tsai, C. (2007) Tuning Parameter Selectors for the Smoothly Clipped Absolute Deviation Method. Biometrika, 94, 553-568.
