Advances in Applied Mathematics
Vol.07 No.05(2018), Article ID:25063,9
pages
10.12677/AAM.2018.75069
A New Method for Calculating the High Order Origin Moments of Classical Probability Models
Jie Xia, Wenqing Wu, Xiaohui Li, Zhiping Wang, Haiyang Lan
School of Science, Southwest University of Science and Technology, Mianyang Sichuan

Received: Apr. 30th, 2018; accepted: May 18th, 2018; published: May 25th, 2018

ABSTRACT
Due to the mathematical complexity of calculating the high order origin moments of classical probabilistic models directly by definition, two methods for calculating the higher order moments are given in this paper. In the method one, considering the expansion of the expression (1 + n)m+1, and applying the mathematical induction method, we obtained the recursive expression of the higher order moments. In the method two, thanks to the can be represented by the representation of m + 1 polynomials, it can be further transformed into an m elements linear system. The expression of the classical model can be found by solving the system of linear equations. Finally, we use the dice test and the English alphabetic experiment as examples to show how to use the two methods.
Keywords:Classical Probability Model, High Order Origin Moment, Recursion Formula, Linear System of Equations
计算古典概型高阶原点矩的新方法
夏杰,吴文青,李晓慧,王志平,兰海洋
西南科技大学理学院,四川 绵阳

收稿日期:2018年4月30日;录用日期:2018年5月18日;发布日期:2018年5月25日

摘 要
考虑直接用定义计算古典概型高阶原点矩的复杂性,本文给出了2种计算古典概型高阶矩的方法。方法一中考虑(1 + n)m+1的二项展开式,应用数学归纳法,得出了古典概型高阶矩的递推表达式。方法二中考虑 可表示成m + 1次多项式的形式,将问题转化为求解m元线性方程组,从而给出古典概型高阶矩的表达式。最后,以掷骰子随机实验和选取英文字母随机实验的高阶原点矩的求解为例具体给出了两种方法的计算过程。
关键词 :古典概型,高阶原点矩,递推公式,线性方程组

Copyright © 2018 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
古典概型也叫传统概率,其定义是由法国数学家拉普拉斯(Laplace)提出的 [1] 。如果一个随机试验只有有限个样本点,且每个样本点发生的可能性均相等,则这个随机试验叫做拉普拉斯试验,这种条件下的概率模型就叫古典概型 [2] 。在实际生活中有很多等概率事件的例子,例如:掷一枚质地均匀的硬币,认为出现正面或反面的可能性是相同的;掷一个质地均匀骰子的实验,出现的六个点数的概率是等可能的;又如对有限件外形和外观相同的产品进行抽样检验,抽到每件产品的概率是相同的。古典概型具有简单、直观、不需要做大量的重复试验的特点,其应用十分广泛,而数学期望,m阶原点矩是随机变量极其重要的特征数 [3] 。因此,研究古典概型的m阶原点矩的计算是十分有意义的。
在概率论与统计中,对于连续型随机变量的m阶原点矩通过利用其对应的分布函数Laplace变换经过求导并在参数为零时即可求得。然而,对于离散型随机变量的m阶原点矩的计算就显得极其困难。在概率论与数理统计、随机过程教材中均没有给出求解离散随机变量高阶原点矩的计算公式或递推表达式。
对于离散随机变量高阶矩的计算现已有大量研究。魏孝章 [4] 利用幂级数逐项积分求和法给出了几何分布的各阶原点矩的方法,从而得出几何分布的某些原点矩的计算结果。何梅等人 [5] 研究了离散型随机变量的高阶矩,给出了几类离散型随机变量的高阶原点矩的统一递推公式,并给出了高阶原点矩的形式特征。于晶贤等人 [6] 将数学中的第二类Stirling数和二项式定理应用到泊松分布高阶原点矩的计算中,得到了泊松分布高阶原点矩的计算公式与递推表达式。于晶贤 [7] 将组合数学中的两个重要恒等式应用到离散随机变量高阶原点矩,并给出了二项分布、负二项分布、超几何分布的高阶原点矩的递推表达式。刘常彪等人 [8] 对超几何分布的高阶原点矩、高阶中心矩及高阶半不变量进行了研究,利用组合数学与概率论的方法得出这3种高阶矩的直接表达式。从上述研究文献可知,学者主要利用组合数学与概率论的方法和第二类Stirling数和二项式定理给出了离散型随机变量的高阶矩。然而,对于古典概型的高阶原点矩,本文利用了2种新方法对它的高阶原点矩的计算问题进行了详细讨论。
本文给出了2种计算古典概型高阶矩的方法。一方面,考虑 的二项展开式,应用数学归纳
法,得出了古典概型高阶矩的递推表达式。另一方面,考虑 可表示成 次多项式,进一步转化
为m元线性方程组,对线性方程组进行求解即可求出古典概型高阶矩的表达式。最后,以掷骰子实验和选英文字母实验为特殊实例,给出了各自的前6阶矩的数值结果。
2. 问题的提出
设某一随机事件有n个样本点,且每个样本点发生的可能性相等。若事件A有p个样本点,则事件A的概率为 。现对n个样本点标号,分别为 ,记随机变量X为任取一个样本点上面的数字,则随机变量X的m阶原点矩分别为:
随机变量X的一阶原点矩:
随机变量X的二阶原点矩:
随机变量X的三阶原点矩:
随机变量X的m阶原点矩:
可见,为了确切地给出 的表达式,关键问题是要计算 的表达式。从上面的推导看出,
当m的取值比较小时,我们是可以很快计算出来的。但是,当m的取值逐渐增大时,求解 就变得异常复杂,直接的求解显然是不大现实的。也正是因为这一原因,所以到目前为止,也鲜有文献报道离散随机变量高阶原点矩的求解。本文针对这一表达式,提出了两种计算其表达式的方法。下面具体给出求解 的详细步骤。
3. 表达式 的计算
3.1. 方法1:数学归纳法
众所周知, 可表示成如下形式:
(1)
进一步,式(1)移项后可得:
(2)
对式(2),分别取不同的n的值,得到下面的表达式,
(3)
式(3)中,等号两边分别相加可得:
(4)
令式(4)中, ,则式(4)可表示为:
(5)
综上,可得 的通项公式为:
(6)
此时,注意到
(7)
由 的通项公式可知,有初值和递推表达式,则 的值即可求解。
3.2. 方法2:线性方程组
为了计算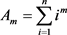 ,我们首先计算
的情形。从图1中可看出,
介于
和
之间,即
,我们首先计算
的情形。从图1中可看出,
介于
和
之间,即
(8)
进一步,式(8)可化为
(9)
如果 存在通项公式,可设 为三次多项式,即
(10)
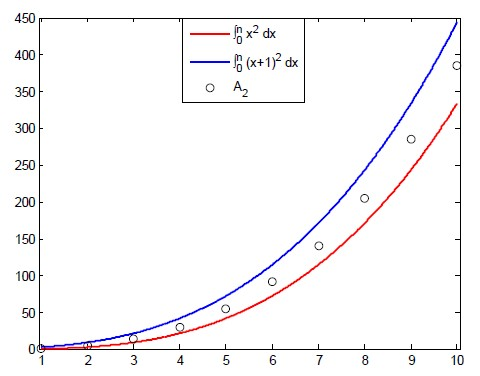
Figure 1. The relationship between and and
图1. 与 和 之间的关系
式(10)中, ,则式(11)可进一步转化为四元一次方程组为
(11)
求解四元一次方程组,得到解为 。于是,式(10)可表示为:
(12)
同理, 满足
(13)
如果 存在通项,则其应有表达式
(14)
则可以通过建立m元一次方程组
(15)
式(15)中只要给定一个确定的m就可求出 。
(16)
其中,
由式(14)可知,只要求出 就可求出 。
4. 实例分析
下面给出两个古典概型高阶原点矩的计算表达式,以此验证我们提出的计算方法的正确性。
1) 掷骰子实验
掷一个质地均匀骰子的实验,出现1,2,3,4,5,6六个点数的概率是等可能的,为古典概型。记 为掷骰子实验出现的点数,其中 ,则每次发生的概率为 。
事实上,它的前6阶原点矩可计算得到
下面我们采用本文提出的方法来计算:
方法一:数学归纳法
当 时, ,可根据方法一式(6)可计算 。
因此,骰子的实验的前6阶矩为:
方法二:线性方程组
由式(14)~(16)可计算出 的通项公式,可得以下表达式:
当 时, 因此,可计算
2) 选英文字母实验
每次敲键盘,出现的 共26个字母的概率是等可能的,为古典概型。记 为敲键盘实验出现的字母,为了方便计算记 ,则每次发生的概率为 。
事实上,它的前6阶原点矩可计算得到
方法一:数学归纳法
当 时, ,可根据方法一式(6)可计算 。
进一步,可计算选英文字母实验的前6阶矩为:
方法二:线性方程组
当 时,因此 ,可计算
从上面两个实例可看出,本文给出的2种计算古典概型高阶矩的计算数值与由定义计算出的古典概型高阶原点矩的数值相等,进一步说明了,本文提出的计算高阶矩的方法具有一定的有效性和实用性。
5. 结论
本文给出了2种计算古典概型高阶矩的方法,得出计算古典概型高阶矩的递推表达式。以掷骰子实验和选英文字母实验为特殊实例,给出了给自的前6阶矩的计算数值。本文研究的工作为古典概型的随机变量高阶矩的计算给出了可行的计算公式,为计算机求解高阶矩带来了方便。
文章引用
夏 杰,吴文青,李晓慧,王志平,兰海洋. 计算古典概型高阶原点矩的新方法
A New Method for Calculating the High Order Origin Moments of Classical Probability Models[J]. 应用数学进展, 2018, 07(05): 584-592. https://doi.org/10.12677/AAM.2018.75069
参考文献
- 1. 李勇, 张淑梅. 古典概型知识结构解析[J]. 数学通报, 2008, 47(7): 4-5.
- 2. 崔向照, 李春. 概率论与数理统计[M]. 北京: 科学出版社, 2016.
- 3. 曹小玲. 浅谈概率论中“数学期望”概念的讲解[J]. 教育教学论坛, 2014, 5(5): 199-201.
- 4. 魏孝章. 关于几何分布的高阶原点矩的探讨[J]. 西安文理学院学报(自然科学版), 2006, 9(1): 66-68.
- 5. 何梅, 朱成莲. 常用离散型随机变量的高阶原点矩[J]. 大学数学, 2009, 25(2): 194-199.
- 6. 于晶贤, 李金秋. 泊松分布高阶原点矩的两种计算方法[J]. 数学的实践与认识, 2010, 40(21): 221-224.
- 7. 于晶贤. 一类离散型随机变量高阶原点矩的递推计算方法[J]. 科学技术与工程, 2010, 10(15): 3681-3683.
- 8. 刘常彪, 王海龙. 关于超几何分布高阶矩的研究[J]. 内蒙古师大学报(自然汉文版), 2014, 43(1): 23-25.