Advances in Applied Mathematics
Vol.
07
No.
10
(
2018
), Article ID:
27253
,
9
pages
10.12677/AAM.2018.710151
A Numerical Solution to a Solution Problem for Elliptic Equation with Variable Coefficients
Duowei Zhu1, Adil Nazakat1, Mamat Imam2, Abduwali Abdirixit1
1College of Mathematics and Systems Science, Xinjiang University, Urumqi Xinjiang
2College of Mathematics and Information, Shaanxi Normal University, Xi’an Shaanxi

Received: Oct. 1st, 2018; accepted: Oct. 17th, 2018; published: Oct. 24th, 2018

ABSTRACT
This paper proposes a numerical solution for solving that problem of fixed solution of the variable coefficient elliptic equation, and we get the corresponding error analysis, the method is verified by numerical experiments; convergence speed and small error, in time and space can achieve second-order accuracy.
Keywords:Variable Coefficient Elliptic Equation, Numerical Solution, The Error Analysis
变系数椭圆型方程定解问题的一种数值解法
朱多薇1,娜扎开提·阿迪力1,伊马木·麦麦提2,阿不都热西提·阿不都外力1
1新疆大学,数学与系统科学学院,新疆 乌鲁木齐
2陕西师范大学,数学与信息学院,陕西 西安

收稿日期:2018年10月1日;录用日期:2018年10月17日;发布日期:2018年10月24日

摘 要
本文提出了一种求变系数椭圆型方程定解问题的数值解法,并进行了误差分析,通过数值实验验证了该方法收敛速度快,误差小,在时间和空间上能达到二阶精度。
关键词 :变系数椭圆型方程,数值解法,误差分析

Copyright © 2018 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
目前关于常系数椭圆型方程定解问题的数值解法已有很多差分格式 [1] - [6] 。而变系数椭圆型方程定解问题的数值解法相对比较复杂,数值解的精度一般比较低,因此构造求解变系数椭圆型方程定解问题的高精度差分格式具有实际意义。在文献 [7] 中讨论了变系数椭圆型方程的紧致差分格式,证明了差分格式解的存在唯一性,稳定性和收敛性。在文献 [8] 中考虑了狄利克雷边界条件的椭圆型方程定解问题。在文献 [9] 中提出了椭圆型方程定解问题的自适应网格的紧凑差分格式,此方法加密网格时大大增加了计算量,而本文利用极坐标下的差分格式建立了一种差分格式–交错五点差分格式,对于求解一类变系数椭圆型方程的定解问题,减少了计算量,得到了相应的误差估计,并进行了数值模拟。我们讨论的问题如下:
(1)
其中 是关于 的变系数函数, 是 的足够光滑的函数,求解区域 ,其边界 为分段光滑曲线。
2. 差分格式的建立
为了推导差分格式,取沿 方向和 方向的步长h和k,做两族分别 轴和 轴平行的直线:
两族直线的交点 称为节点。若两个节点沿 轴方向(或 轴方向)只相差一个步长时,称两个节点是相邻的。以 表示所有属于 内部的节点集合,并称此类点为内节点。
以 表示网格线 或 与 的交点的集合,并称此类点为边界节点。
记 上的网格函数为:
其中
2.1. 交错五点差分格式
把问题(1)用极坐标下的差分格式:
(2)
离散 [10] ,其中 , ,整个 平面映射为 平面上的半带型域 分两步离散:
第一步,对问题(1)中的 ,先把括号外面的一阶微分 用半个步长的中心差分代替。即
第二步,把第一步离散后的微分再用半个步长的中心差分代替,可得到问题(1)中的每一个微分项的离散格式如下:
(3)
(4)
(5)
(6)
其中变系数函数 在半个步长上的值为
以上离散格式(3),(4),(5),(6)略去高阶项后代入到问题(1)得到如下差分格式:
(7)
其中 。
差分格式(7)是由节点和剖分所形成的网格的中心
(称为网格的中心点)交错得到的,从节点的角度看,用了五个节点 ,但是计算的时候我们用到了网格的中心点,又可以看作是九个点的差分格式。因此,我们称差分格式(7)为交错五点差分格式。
2.2. 五点差分格式
观察差分格式(7),我们需要计算节点和网格的中心点,计算量比较大。因此,我们用中点公式把网格的中心点转化到节点上。如下:
(8)
(9)
(10)
(11)
把所有网格的中心点都转化到节点上,这样方便计算,就得到较简单的五点差分格式:
(12)
五点差分格式(12)简单,易于编程实现,并且很容易推广到其它复杂情形。由于交错五点差分格式(7)具备九点差分格式的特点,我们可以构造一般的九点差分格式,对比研究新格式(7)。以下是构造的一般九点差分格式。
2.3. 九点差分格式
同交错五点差分格式的离散一样,把问题(1)也用极坐标下的差分格式(2)进行离散,但是每个微分项不都用半个步长的中心差分来离散,构造以下九点差分格式时,微分项 与交错五点差分格式的离散一样,分两步,每一步都是用了半个步长的中心差分离散 [10] ,而微分项 分两步离散时 [11] ,都是用了一个步长的中心差分,因此,得到问题(1)的每一个微分项的离散格式如下:
(13)
(14)
(15)
(16)
以上离散格式(13),(14),(15),(16)略去高阶项代入到问题(1)得到如下九点差分格式:
(17)
以下分别讨论三种差分格式的误差。
3. 差分格式的误差分析
我们考虑的是变系数椭圆型方程的定解问题,对于交错五点差分格式(7)来说,用微分方程的解 来代替差分格式(7)中的近似解 这样就得到问题两边的差 在点 处Taylor 展开代入差分格式)就是截断误差:
(18)
其中 。
同理,可得到一般的五点差分格式(12)的截断误差如下:
(19)
其中 。
同理,可得到一般九点差分格式(17)的截断误差如下:
(20)
其中 。
由截断误差的讨论可知,只要网格剖分得很细,即 很小,那么问题(1)的解近似地满足相应的差分格式(7),(12),(17)。因此根据上面的计算,三种差分格式的截断误差为 ,即三种格式都是二阶精度的。
4. 数值例子
为了数值实验,我们考虑如下问题:
(21)
我们在 上计算,准确解为 。在Matlab坏境下编程实现。
我们用交错五点差分格式,一般五点差分格式和一般九点差分格式求解上述例子,分别用Gauss-Seidel迭代法和SOR迭代法解线性方程组,得到数值计算结果如下所示。
表1反映了三种差分格数值解和准确解的计算结果,从表中可以看出,交错五点差分格式与准确解最接近,能很好的保持解原来的面貌。九点差分格式与准确解也比较相似,但是没有交错五点差分格式所求的解准确,一般五点差分格式,从表格中可以看出,误差相对于交错五点差分格式和一般九点差分格式来说比较大,所以交错五点差分格式更具有一般九点差分格式的特点,计算的数值解更准确。
其中KG是用Gauss-Seidel迭代法计算的迭代次数,KS是用SOR迭代法计算的迭代次数。
表2是三种差分格式用Gauss-Seidel迭代法,SOR迭代法求解的结果,不管是Gauss-Seidel迭代法,还是SOR迭代法,从表中可以看出一般五点差分格式比九点差分格式和交错五点差分格式所迭代的次数少,一般九点差分格式比交错五点差分格式迭代的次数少,说明虽然交错五点差分格式求出的解更准确,但是计算量较大,还需要我们对交错五点差分格式的算法进一步研究。
Table 1. Exact solution and numerical solution of three difference schemes
表1. 三种差分格式的数值解和准确解的计算结果
表3是三种差分格式最大误差与误差阶的计算结果,从表中可以看出交错五点差分格式的误差小,收敛速度最快,随着网格地加密,收敛阶逐渐趋向二阶,与理论预期的结果一致,九点差分格式结果也是比较理想的,但是收敛速度比交错五点差分格式的慢一些,其误差阶也趋于二阶,与理论结果保持一致。五点差分格式收敛速度较慢,最终误差趋于一个稳定的值。
取 ,即 ,用上述的三种差分格式解问题(1),得到的准确解与数值解的图像如图1。
图1可以看出准确解与三种差分格式所得的数值解非常接近,图像面貌基本一致,说明这三种差分格式对本文所求问题的数值解有效。
下面给出三种差分格式的误差图。
取 ,即 ,用上述的三种差分格式求解问题(1),得到准确解与数值解的误差如图2。
图2是三种差分格式的误差图,从图中可以看出,五点差分格式的误差明显比九点差分格式的误差大。从图2中我们还可以看出五点差分格式最大误差来源于内节点,九点差分格式的最大误差来源于边界节点,而交错五点差分格式的误差是由交错点之间计算产生的。
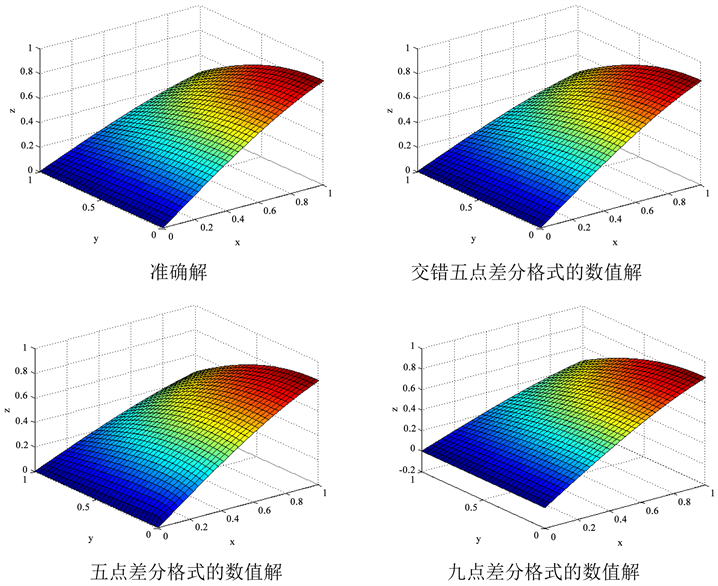
Figure 1. M = N = 32, Exact solution and numerical solution of three difference schemes
图1. M = N = 32准确解与三种差分格式的数值解
Table 2. The number of iterations calculated by Gauss-Seidel and SOR iterative methods in three difference schemes
表2. 三种差分格式用Gauss-Seidel迭代法和SOR迭代法求解的迭代次数
Table 3. Error and error order of three difference schemes
表3. 三种差分格式的误差和误差阶

Figure 2. Error of three difference schemes
图2. 三种差分格式的误差
5. 结论
本文提出了变系数椭圆型方程定解问题的交错五点差分格式,并与九点差分格式和五点差分格式进行了比较,数值实验结果表明交错五点差分格式比其他两种格式效果更好,误差更小,收敛速度更快。我们建议,在求解有交叉项的变系数椭圆型定解问题时优先选择交错五点差分格式。
基金项目
国家自然科学基金资助项目(10971024)。
文章引用
朱多薇,娜扎开提·阿迪力,伊马木·麦麦提,阿不都热西提·阿不都外力. 变系数椭圆型方程定解问题的一种数值解法
A Numerical Solution to a Solution Problem for Elliptic Equation with Variable Coefficients[J]. 应用数学进展, 2018, 07(10): 1299-1307. https://doi.org/10.12677/AAM.2018.710151
参考文献
- 1. 苏铭德. 用半直接法数值求解一类椭圆型方程[J]. 高等学校计算数学学报, 1984(3): 26-35.
- 2. 何跃. 一类退化椭圆型方程边值问题的适定性[J]. 数学年刊A辑, 2007, 28(5): 651-666.
- 3. 韩丕功. 关于半线性椭圆型方程和方程组的研究[J]. 中国科学院研究生院学报, 2009, 26(1): 141-143.
- 4. Douglas, J. (1962) Alternating Discriminant Methods for Three Space Variable. Numerische Mathematik, 4, 41-63. https://doi.org/10.1007/BF01386295
- 5. Peaceman, D.W. and Rachford, H.H. (1955) The Numerical Solution of Parabolic and Elliptic Difference Equation. Journal of the Society for Industrial and Applied Mathematics, 3, 28-41.
- 6. Hou, S. and Liu, X.D. (2005) A Numerical Method for Solving Variable Coefficient Elliptic Equation with Interfaces. Journal of Computational Physics, 202, 411-445. https://doi.org/10.1016/j.jcp.2004.07.016
- 7. 孙岩刚. 变系数椭圆型方程的紧差分格式[D]: [硕士学位论文]. 沈阳: 东北大学, 2008.
- 8. Mohamed, N.A., Mohamed, N.F, Mohamed, N.H., et al. (2016) Numerical Solution of Dirichlet Boundary-Domain Integro-Differential Equation with Less Number of Collocation Points. Applied Mathematical Sciences, 10, 2459-2469. https://doi.org/10.12988/ams.2016.6381
- 9. Raeli, A., Bergmann, M. and Iollo, A. (2017) A Finite-Difference Method for the Variable Coefficient Poisson Equation on Hierarchical Cartesian Meshes. Journal of Computational Physics, 355, 59-77. https://doi.org/10.1016/j.jcp.2017.11.007
- 10. Gupta, H.S. (2012) A Numerical Study of Variable Coefficient Elliptic Cauchy Problem via Projection Method. International Journal of Computer Mathematics, 89, 795-809. https://doi.org/10.1080/00207160.2012.659426
- 11. Ang, W.T., Kusuma, J. and Clements, D.L. (1995) A BIE for a Second Order Elliptic Partial Differential Equation with Variable Coefficients. Computational Mechanics. Springer Berlin Heidelberg, 2683-2688.
