Advances in Applied Mathematics
Vol.
09
No.
01
(
2020
), Article ID:
33941
,
6
pages
10.12677/AAM.2020.91011
Research on the Cross Entropy Optimization Method Evaluation Based on the Three Typical Functions
Yan Li, Wenqiang Luo, Jingyun Lu
School of Mathematics and Physics, China University of Geosciences, Wuhan Hubei
Received: Dec. 23rd, 2019; accepted: Jan. 7th, 2020; published: Jan. 14th, 2020

ABSTRACT
The cross entropy optimization method is transformed from the cross entropy method to estimate the probability of failure. By constructing the artificial reliability problem, it concentrates the problem on the search of the maximum value, and then the minimum value of the function can be solved. According to three typical functions, the test results of the cross entropy optimization method are compared with those of the genetic algorithm. The results show that the global convergence rate and accuracy of the cross entropy optimization method are better than the genetic algorithm for single-peak and multi-peak functions. For this Pathological function, which is difficult to minimize globally, the cross entropy optimization method also overcomes the problem of local optimization, and the optimization result is closer to the theoretical optimal value.
Keywords:Cross Entropy, Genetic Algorithm, Optimization

基于三个典型函数的交叉熵优化方法评价研究
李燕,罗文强,卢静云
中国地质大学数学与物理学院,湖北 武汉
收稿日期:2019年12月23日;录用日期:2020年1月7日;发布日期:2020年1月14日

摘 要
本文介绍了从估计失效概率的交叉熵法转化而来的交叉熵优化方法。它通过构建人工可靠性问题,将问题聚集在最值搜索上,从而求出函数的最小值。本文根据三个典型函数的测试结果,并将其与遗传算法的运算结果进行对比,结果表明交叉熵优化方法在单峰和多峰函数的全局收敛速度和精确度均优于遗传算法,对于难以全局极小化的病态函数,交叉熵优化方法也克服了局部最优的问题,其优化结果更接近于理论最优值。
关键词 :交叉熵,遗传算法,优化

Copyright © 2020 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
交叉熵(Cross Entropy,CE)优化方法的思想来源于信息论中的概念,即Kullback-Leibler距离。1997年,Rubinstein最先将交叉熵算法应用于小概率事件估计,提出重点采样(Importance Sampling,IS)策略,而后将其发展成为一种随机优化方法,从此交叉熵优化算法被广泛地应用于解决复杂优化问题 [1]。2001年,Helvik和Wittner改进交叉熵方法后将其运用于寻找智能主体网络最优路径,证明交叉熵方法拥有很好的收敛性 [2]。2005年,Alon等在解决高校优化缓冲区分配问题时,运用了交叉熵优化方法,结果证明该方法计算效率非常高 [3]。2015年,Ghidey采用了交叉熵方法和其他可靠性方法来解决可靠性优化设计问题,实验结果证明交叉熵方法在精度和效率上都更具有优势 [4]。综上所述,交叉熵方法具有计算效率高和收敛性好的优点,在网络可靠性分析 [2] 、可靠性优化设计问题 [4] 、车辆路径 [5] 等领域内广泛应用,并且针对其缺陷有了相应改进 [6] [7]。但是交叉熵优化方法仅仅应用于具体的实际问题,目前缺乏针对理论最优解已知函数的实验,因此仍需针对这个问题进一步探究交叉熵优化方法的收敛性和计算效率,从而对交叉熵优化算法进行科学评价。因此本文利用三个典型函数,并将交叉熵优化方法与遗传算法的运算结果进行对比,结果证明交叉熵优化方法在单峰和多峰函数的全局收敛速度和精确度均优于遗传算法,对于难以全局极小化的病态函数,交叉熵优化方法也克服了局部最优的问题,其优化结果更接近于理论最优值。
2. 原理
可靠性分析的目的是评估一个事件F发生的可能性大小,而优化问题的目的是搜索一个点或者区域,使得目标函数取得极值。如图1以求函数f最大值为例,可以发现优化问题和可靠性问题是存在一部分相似的。如果将设计变量x作为随机变量,则可定义一个新的可靠性问题即评估函数f超过给定阈值 的概率 。工程可靠性问题通常是一个稀疏事件模拟问题,也就是一个小概率事件。所以极值事件可认为是稀疏事件的一种特殊情况,因此优化问题和可靠性问题之间可转化,转化原理如图2。人为构造可靠性问题的目的并不是计算失效概率,而是为了搜索满足 函数的值,然后就可以求出失效概率相对应的最大值 及解 。
交叉熵优化方法是从估计失效概率的交叉熵法转化而来的,其基本思想为:构建人工可靠性问题,将问题聚集在最值搜索上,而不是失效概率的估计,从而求出实值函数 的最小值,即
(1)
假设函数 的最小值为 ,即
 (2)
(2)
则可构建一个可靠性问题为
(3)
式(3)是一个特殊的可靠性问题,当聚集在最值搜索上时,如图2所示,此时 。因此优化问题可以通过式(3)转化为可靠性问题,然后采用交叉熵方法对式(3)求解。但是使用交叉熵方法时,并不会事先指定失效事件及响应函数的阈值,在迭代过程中概率密度函数
最终收敛到一个最优概率密度函数
,然后得到最优概率密度函数的函数值会在最优解
上或附近。当中间失效事件的阈值
接近或者等于最优值
时,概率密度函数
会赋予最优解
附近点很大的概率值,则此时该概率密度函数随机抽取的任意样本可以认为是最优解
的逼近值,并且对应的函数
的值逼近最优值。
。因此优化问题可以通过式(3)转化为可靠性问题,然后采用交叉熵方法对式(3)求解。但是使用交叉熵方法时,并不会事先指定失效事件及响应函数的阈值,在迭代过程中概率密度函数
最终收敛到一个最优概率密度函数
,然后得到最优概率密度函数的函数值会在最优解
上或附近。当中间失效事件的阈值
接近或者等于最优值
时,概率密度函数
会赋予最优解
附近点很大的概率值,则此时该概率密度函数随机抽取的任意样本可以认为是最优解
的逼近值,并且对应的函数
的值逼近最优值。

Figure 1. Similarities between optimization problems and reliability problems
图1. 优化问题与可靠性问题间的相似点
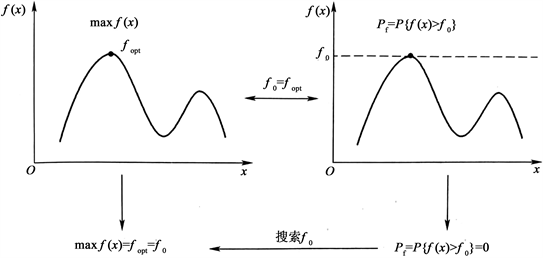
Figure 2. The transition between optimization problems and reliability problems
图2. 优化问题和可靠性问题之间的转化
3. 方法步骤
交叉熵优化方法的步骤如下:
1) 初始化待定分布参数 ,迭代记数 。
2) 从 产生N个随机样本 ,代入函数中求值 并排序,依据式 确定的值,其中 为功能函数次序统计量的 分位数, 为从小到大排序后的统计量,即 为N个样本中最小值, 为N个样本中最大值。
3) 使用同样的N个随机样本
,解式
,设权函数 ,从而得
新的参数的估计值
。
,从而得
新的参数的估计值
。
4) 若达到某种收敛准则,算法停止,否则设 ,转步骤(2)。
4. 实验分析
本文将根据三个典型函数优化问题以求最小值为例来评价交叉熵优化算法,并且与遗传算法(Genetic Algorithm,GA)的实验结果进行比较。其中,函数 是单峰二次函数,极小值点只有一个;函数 是一个具有强烈震荡的多峰函数;函数 是单峰函数,同时是一个病态的二次函数,很难全局极小化。实验设置的参数如下:交叉熵的光滑参数为0.9,稀薄参数为0.1,精度参数为10−4,单层样本量为500。遗传算法的交叉概率为0.8,变异概率为0.05,算法最大迭代次数为5000。用交叉熵优化方法和遗传算法求解上述优化问题运行20次,得到平均函数最优解和迭代次数,实验结果如表1所示。
(4)
(5)
(6)
Table 1. The average optimal value of a function that runs 20 times
表1. 两种算法运行20次的函数平均最优值
表1中三个测试函数的理论最小值都是零点,交叉熵优化方法运行20次最优解均值都小于遗传算法的最优解均值,更接近于理论最优值。对于函数 ,交叉熵的迭代次数更少。对于函数 ,交叉熵优化方法和遗传算法的迭代次数相近,对于函数 ,遗传算法在大多数情况下迭代次数少于交叉熵优化方法。但是,从表1中可以发现遗传算法的实验迭代次数最大值达到了迭代停止条件,说明遗传算法在优化 函数问题时陷入了局部最优。因此从表1的实验数据可以发现,交叉熵优化方法的优化结果明显好于遗传算法。图3、图4、图5为交叉熵优化方法和遗传算法对于三个测试函数的最优值迭代曲线,横轴为迭代次数,纵轴为函数最优值。从图3和图4可以发现,交叉熵优化方法的迭代曲线相比于遗传算法的迭代曲线下降更快,并且更接近于理论最优值。因此证明了对于单峰和多峰函数,交叉熵优化方法的收敛速度相较于遗传算法更快,且更接近理论最优值。在图5中,遗传算法的迭代曲线下降更快,收敛速度较于交叉熵方法更快,但是结合表1可以发现,遗传算法曾出现陷入了局部最优的情况,而使用交叉熵优化方法虽然增加了计算量,却克服了局部最优的问题,对于函数 的优化结果更稳定,更接近最优值。总而言之,交叉熵优化方法相比遗传算法对这三个典型函数的优化结果更好。
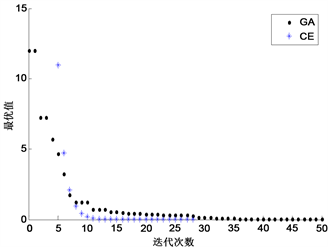
Figure 3. The optimal value iteration curve of function
图3. 最优值迭代曲线

Figure 4. The optimal value iteration curve of function
图4. 最优值迭代曲线
最优值迭代曲线

Figure 5. The optimal value iteration curve of function
图5. 最优值迭代曲线
5. 结论
本文利用三个测试函数,针对交叉熵优化方法和遗传算法的测试结果进行了比较,结果表明:对于单峰和多峰函数,交叉熵优化方法的全局收敛速度和精确度均优于遗传算法;对于难以极小化的病态函数,交叉熵优化方法虽然增加了计算量,但是克服了局部最优的问题,实验运行结果相比遗传算法更稳定,更接近于理论最优值。
文章引用
李 燕,罗文强,卢静云. 基于三个典型函数的交叉熵优化方法评价研究
Research on the Cross Entropy Optimization Method Evaluation Based on the Three Typical Functions[J]. 应用数学进展, 2020, 09(01): 94-99. https://doi.org/10.12677/AAM.2020.91011
参考文献
- 1. Rubinstein, R. (1999) The Cross-Entropy Method for Combinatorial and Continuous Optimization. Methodology & Computing in Applied Probability, 1, 127-190.
https://doi.org/10.1023/A:1010091220143 - 2. Helvik, B.E. and Wittner, O. (2001) Using the Cross-Entropy Method to Guide/Govern Mobile Agent’s Path Finding in Networks. In: Pierre, S. and Glitho, R., Eds., Mobile Agents for Telecommunication Applications, Springer, Berlin, Heidelberg, 255-268.
https://doi.org/10.1007/3-540-44651-6_24 - 3. Alon, G., Kroese, D.P., Raviv, T., et al. (2005) Application of the Cross-Entropy Method to the Buffer Allocation Problem in a Simulation-Based Environment. Annals of Operations Research, 134, 137-151.
https://doi.org/10.1007/s10479-005-5728-8 - 4. Ghidey, H. (2015) Reliability-Based Design Optimization with Cross-Entropy Method. Ph.D. Thesis, Norwegian University of Science and Technology, Norway.
- 5. Chepuri, K. and Homem-De-Mello, T. (2005) Solving the Vehicle Routing Problem with Stochastic Demands Using the Cross-Entropy Method. Annals of Operations Research, 134, 153-181.
https://doi.org/10.1007/s10479-005-5729-7 - 6. Kroese, D.P., Porotsky, S. and Rubinstein, R.Y. (2006) The Cross-Entropy Method for Continuous Multi-Extremal Optimization. Methodology and Computing in Applied Probability, 8, 383-407.
https://doi.org/10.1007/s11009-006-9753-0 - 7. 任超, 张航, 李洪双. 随机优化的改进交叉熵方法[J]. 北京航空航天大学学报, 2018, 44(1): 205-214.
