Advances in Applied Mathematics
Vol.
10
No.
04
(
2021
), Article ID:
41613
,
14
pages
10.12677/AAM.2021.104099
具有阶段结构和Allee效应的捕食–食饵模型的随机动力学分析
冯赛提,张天四
上海理工大学理学院,上海
收稿日期:2021年3月14日;录用日期:2021年4月3日;发布日期:2021年4月16日

摘要
本文研究了一类具有阶段结构和Allee效应的捕食–食饵模型的随机动力学行为。首先,我们讨论的模型是由3个随机微分方程构成,它主要描述了食饵、未成熟捕食者和成熟捕食者之间的相互作用。其次,为了证明模型存在全局唯一正解,我们构造多个合适的李雅普诺夫函数,并建立了系统存在遍历平稳分布的条件。最后,我们建立了食饵和两个捕食者灭绝的条件。
关键词
捕食–食饵模型,Allee效应,随机,阶段结构,平稳分布,灭绝
Stochastic Dynamics Analysis of a Predator-Prey Model with Stage Structure and Allee Effect
Saiti Feng, Tiansi Zhang
College of Science, University of Shanghai for Science and Technology, Shanghai
Received: Mar. 14th, 2021; accepted: Apr. 3rd, 2021; published: Apr. 16th, 2021

ABSTRACT
In this paper, the stochastic dynamics of a predator-prey model with stage structure and Allee effect is handled and established based on some suitable Lyapunov functions. First of all, our model is composed of three random differential equations, which describes the interaction between predator species and prey. Secondly, to prove the existence of a globally unique positive solution to the model, we construct several appropriate Lyapunov functions, and then establish the conditions for the existence of ergodic stationary distribution for the system. Finally, we establish the extinction conditions for the prey and two species of predator.
Keywords:Predator-Prey Model, Allee Effect, Stochastic, Stage Structure, Stationary Distribution, Extinction

Copyright © 2021 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 介绍
在生态学的研究过程中,由于捕食者和食饵是普遍存在的,因此捕食者与被捕食者之间的相互作用及其关系是一个研究的热点问题之一。第一个捕食食饵模型是由Lotka [1] 和Volterra [2] 提出的,自从著名的Lotka-Volterra模型被提出以来,捕食者与食饵之间关系研究一直是生物学家和数学家等学者们研究的重点。为了更真实地反应捕食者和食饵之间的关系,更贴合真实的生态系统,学者们在捕食–食饵模型中引入了多种功能反应,并对其做了大量的研究,得到了丰富的结论 [3] [4] [5] [6]。
然而,在我们建立模型时有一个很重要的影响因素Allee效应,也是值得考虑的。Allee效应是由Allee [7] 提出来的,并以他的名字命名,他对种群的影响很显著。Allee效应表示的是个体适应性与种群密度之间的正相关关系 [8] [9]。近些年来,将Allee效应引入到捕食–食饵模型中引起了学者们的关注,并对其做了大量研究 [3] [10] - [16],得到了一些新的结论,丰富了生物数学的研究。
但是在我们的生态系统中,生态系统的种群存在是很复杂的,有未成熟种群逐渐转化为成熟种群,这种阶段变化可以更好地反应种群的生长和相互关系,更能真实地体现生态系统的瞬息万变。此外,很多学者做了很多关于具有阶段结构的捕食–食饵系统的动力学研究 [17] - [23]。Xiao在 [17] 研究了带有时滞和Allee效应具有阶段结构的捕食–食饵模型,证明了平衡点的稳定性以及产生分支的情况。蒋达清在参考文献 [24] 中提出了具有Holling Type II的阶段结构的捕食–食饵模型,得到了模型在存在遍历平稳分布以及捕食者灭绝的结论。针对此,我们提出了具有阶段结构和Allee效应的捕食–食饵的确定性模型:
(1.1)
其中
分别表示食饵种群,未成熟捕食者种群,成熟捕食者种群在t时刻的密度,m表示捕获率,n是捕食者的食物转化率,
和e分别表示未成熟和成熟捕食者的死亡率,
表示未成熟捕食者变成成熟捕食者速度,其中
均为正常数。
然而,在现实生活中,大多数现象无法用确定性的规律来解释,而总是受到环境噪声的影响。当把环境噪声引入到模型中时,我们发现它可以更好地预测未来生态系统模型的发展。许多学者研究了带有环境噪声的随机捕食–食饵模型 [5] [6] [24] [25] [26],Zhao在文献 [26] 中考虑了具有阶段结构的随机捕食–食饵模型,给出了系统存在平稳分布的充分条件,同时给出了捕食者灭绝的条件。因此,为了更好地讨论具有阶段结构和Allee效应的捕食食饵模型,我们引入了环境噪声,模型如下:
(1.2)
其中
,, 为标准布朗运动,
为噪声强度。本文的研究主要分为以下几个部分:第二部分,介绍与本篇文章相关的预备知识;第三部分,证明系统(1.2)存在全局唯一正解;第四部分,建立了系统(1.2)存在平稳分布的条件;第五部分,证明了系统(1.2)捕食者
和食饵x灭绝的条件;最后对全文做了总结和期望。
2. 预备知识
在本部分,我们介绍了一些关于随机微分方程的基础知识和基本定理,在我们接下来的证明过程都会用到。
表示一个带有过滤的完全概率空间,其中
满足条件(即
包含所有
-空集,它是递增和右连续的)。我们引入定义
和
考虑一个d维的随机微分方程的马尔可夫过程,
(2.1)
初始值
, 表示定义在完全概率空间
上的d维标准布朗运动。用
表示定义在
上的非负函数
,使得它们在X上连续可微两次。公式(2.1)的微分算子L由 [27] 定义
(2.2)
如果将L作用在
,则可以得到
,
其中
,。利用Itô’s公式 [27] 可得到,如果
,则有
(2.3)
定义2.1. [28] 过渡概率函数
被称为时间齐次函数(相应的Markov过程称为时间齐次函数),如果
是独立于s,
,,, 表示在
中的Borel集的
代数。
令
为随机微分方程中描述的
中的正则时齐马尔可夫过程
.
的扩散矩阵为
,。
引理2.1. [28] 马尔可夫过程
有一个唯一的遍历平稳分布
,如果存在一个有界开域
,常规边界
,具有下列性质:
(B.1):存在一个正数M使
,,。
(B.2):存在一个非负C2-V函数,使LV在任何
上是负的。
3. 正解的存在性和唯一性
在本章节中,我们主要研究系统(1.2)存在正解并证明其正解是唯一的,对于系统(1.2)我们可以清楚的知道
为食饵,未成熟捕食者和成熟捕食者的密度,则它们均为非负常数,且其系数满足局部Lipschitz条件,所以系统(1.2)存在局部解
,,其中
表示爆炸时间。因此,我们只需要证明系统(1.2)存在唯一正解以及正解是全局的,即证
。为此,我们给出如下定理:
定理3.1. 对于任意初始值
,系统(1.2)在
时存在唯一的全局正解,并且解始终以概率1在
。
证明:对于一个足够大的非负数
,使得
, 以及
始终在
这个区间内,对于每个整数
,定义停时 [27]
在这篇文章中
,当
时,显然可以知道
是递增的。令
, (a.s.)。如果我们可以证明
,a.s.则可以得到
, a.s.对于
。因此,为了完成证明,我们只需证明
a.s.如果
,则存在常数
,,使
因此存在一个常数
,使
, (3.1)
定义一个C2函数
(3.2)
对上述V函数利用Itô’s公式 [27] 可得
(3.3)
令
,公式(3.3)则有
(3.4)
其中K为正常数,因此可以得到:
(3.5)
对公式(3.5)从0到
两边积分,并取期望可得
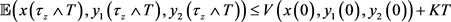 (3.6)
(3.6)
对于
,设
,由公式(3.1)可以得到
。对于每个
, 或
或
等于z或
。因此,可以得到
(3.7)
(3.8)
其中
表示
的指标函数,当
时,可以得到
这就导致了矛盾,故我们可以得到
a.s.证毕。
4. 遍历平稳分布的存在
因为当随机扰动加入确定性模型时,系统的稳定性会被破坏,从而模型会出现随机弱稳定的特性,从而引起了很多研究者们的关注 [29] [30] [31] [32]。在本节中,我们通过构造李雅普诺夫函数,证明了系统(1.2)存在平稳分布。
定理4.1. 如果
,,则对于系统(1.2)的任意给定的初始值
,都存在唯一的遍历平稳分布。
证明:为了证明系统(1.2)存在遍历平稳分布,只需证明引理2.1两个条件成立即可。通过题意,显然可以得到系统(1.2)的扩散矩阵为
(4.1)
对于任意的
,,其中
,引理2.1中的条件(B.1)得证。现在我们证明条件(B.2)。为了证明条件(B.2),我们构造李雅普诺夫函数
,,
,,
其中
是一个足够小的正常数,
为正常数,其中
(4.2)
(4.3)
分别对上述V函数利用Itô’s公式可得,
(4.4)
则有
则对(4.4)利用不等式可得
(4.5)
(4.6)
(4.7)
(4.8)
(4.9)
下面我们定义一个C2的函数
,则有
则根据(4.5)~(4.9)可以得到
(4.10)
为了证明引理2.1中的条件(B.2),我们只需要构造一个有界开集
,定义有界开集
为
,证明
在
成立,其中
是足够小的常数,且满足如下条件:
(4.11)
(4.12)
(4.13)
(4.14)
(4.15)
(4.16)
(4.17)
(4.18)
(4.19)
下面,为了证明
,我们把
分为6个区域,
,,
,,
,
显然,
,接下来证明对于任意的
有
,这等价于分别在上述六个域上证明它。
情况1:对于任意的
,我们可以得到
(4.20)
因此可以得到对于任意的
有
。
情况2:对于任意的
,我们得到
(4.21)
因此可以得到对于任意的
有
。
情况3:对于任意的
,我们得到
(4.22)
因此可以得到对于任意的
有
。
情况4:对于任意的
,我们得到
(4.23)
因此可以得到对于任意的
有
。
情况5:对于任意的
,我们得到
(4.24)
因此可以得到对于任意的
有
。
情况6:对于任意的
,我们得到
(4.25)
因此可以得到对于任意的
有
。
综上,通过公式(4.17)~(4.25),我们可以得到对于足够小的
,对所有的
,,因此引理(3.1)中的(B.2)满足,故通过引理2.1我们可知系统(1.2)具有唯一的遍历平稳分布。
5. 灭绝
这一部分,我们讨论了捕食者和食饵均灭绝的情况。
定理5.1. 若
是系统(1.2)的解,且其初始值为
,如果满足条件
则食饵x,未成熟捕食者
和成熟捕食者
均灭绝。
证明:对于系统(1.2)的第一个式子利用Itô’s公式,可以得到
(5.1)
对公式(5.1)从0到t积分,并两边同时除t
(5.2)
对公式(5.2)取上确界,利用局部鞅的强大数定理 [27],可以知道
几乎是处处成立的,
(5.3)
即
,食饵灭绝。
因此,对于任意小的
,存在
和一个集合
使得
,对于
,, 成立。接下来,证明捕食者
和
灭绝,我们对
利用Itô’s积分
(5.4)
对公式(5.4)两边从0到t积分,并两边同时除t,
(5.5)
对公式(5.5)取上确界,利用局部鞅的强大数定理 [27],可以知道
, 几乎是处处成立的,则有
(5.6)
即
, 捕食者
和
灭绝。
6. 结论
本文主要研究了具有Allee效应和阶段结构的捕食–食饵模型随机动力学行为。首先,我们通过构造恰当的李雅普诺夫函数,建立了系统(1.2)存在全局唯一正解,并得到了系统存在遍历平稳分布的充分条件。此外,我们得到了食饵、未成熟捕食者和成熟捕食者灭绝的条件。得到了一系列的结果:
当
, 时,系统存在唯一的遍历平稳分布;当
时,食饵和捕食者均会灭绝。
当然,在整个生态系统中,会受到很多自然因素和人类的干预,因此捕食–食饵模型还是有很多值得研究的问题。例如,我们可以考虑脉冲效应等,这些都可以在以后的研究中加以思考和解决。
文章引用
冯赛提,张天四. 具有阶段结构和Allee效应的捕食–食饵模型的随机动力学分析
Stochastic Dynamics Analysis of a Predator-Prey Model with Stage Structure and Allee Effect[J]. 应用数学进展, 2021, 10(04): 909-922. https://doi.org/10.12677/AAM.2021.104099
参考文献
- 1. Lotka, A. (1925) The Elements of Physical Biology. Williams and Wilkins, Baltimore.
- 2. Volterra, V. (1926) Fluctuations in the Abundance of Species Considered Mathematically. Nature, 118, 558-560.
https://doi.org/10.1038/118558a0
- 3. Cai, Y.L., Zhao, C.D. and Wang, W.M. (2015) Dynamics of a Leslie-Gower Predator-Prey Model with Additive Allee Effect. Applied Mathematical Modelling, 39, 2092-2106. https://doi.org/10.1016/j.apm.2014.09.038
- 4. Tian, B.D., Yang, L. and Zhong, S.M. (2015) Global Stability of a Stochastic Predator-Prey Model with Allee Effect. Applied Mathematical Modelling, 8, 1550044. https://doi.org/10.1142/S1793524515500448
- 5. Liu, Q., Jiang, D.Q., Ahmad, B. and Hayat, T. (2018) Stationary Distribution and Extinction of a Stochastic Predator-Prey Model with Additional Food and Nonlinear Perturbation. Applied Mathematics and Computation, 320, 226-239. https://doi.org/10.1016/j.amc.2017.09.030
- 6. Xu, D.S., Liu, M. and Xu, X.F. (2020) Analysis of a Stochastic Predator-Prey System with Modified Leslie-Gower and Holling-Type IV Schemes. Physica A: Statistical Mechanics and its Applications, 537, 122761.
https://doi.org/10.1016/j.physa.2019.122761
- 7. Allee, W.C. (1931) Animal Aggregations: A Study in General Sociology. The University of Chicago Press, Chicago.
https://doi.org/10.5962/bhl.title.7313
- 8. Andrew, M.K., Brian, D., Andrew, M.L. and John, M.D. (2009) The Evidence for Allee Effects. Population Ecology, 51, 341-354.
- 9. Franck, C., Lude, B. and Joanna, G. (2008) Allee Effects in Ecology and Conservation. Oxford University Press, Oxford.
- 10. Wang, J.F., Shi, J.P. and Wei, J.J. (2011) Predator-Prey System with Strong Allee Effect in Prey. Journal of Mathematical Biology, 62, 291-331. https://doi.org/10.1007/s00285-010-0332-1
- 11. Lin, Q. (2018) Allee Effect Increasing the Final Density of the Species Subject to the Allee Effect in a Lotka-Volterra Commensal Symbiosis Model. Advances in Difference Equations, 2018, Article No. 196.
https://doi.org/10.1186/s13662-018-1646-3
- 12. Lin, Q.F. (2018) Stability Analysis of a Single Species Logistic Model with Allee Effect and Feedback Control. Advances in Difference Equations, 2018, Article No. 190. https://doi.org/10.1186/s13662-018-1647-2
- 13. Chen, B.G. (2018) Dynamic Behaviors of a Commensal Symbiosis Model Involving Allee Effect and One Party Can Not Survive Independently. Advances in Difference Equations, 2018, Article No. 212.
https://doi.org/10.1186/s13662-018-1663-2
- 14. Biswas, S., Pal, D., Mahapatra, G.S. and Samanta, G.P. (2020) Dynamics of a Prey-Predator System with Herd Behaviour in Both and Strong Allee Effect in Prey. Biophysics, 65, 826-835. https://doi.org/10.1134/S0006350920050036
- 15. Lai, L.Y., Zhu, Z.L. and Chen, F.D. (2020) Stability and Bifurcation in a Predator-Prey Model with the Additive Allee Effect and the Fear Effect. Mathematics, 8, 1280. https://doi.org/10.3390/math8081280
- 16. Zu, J. (2013) Global Qualitative Analysis of a Predator-Prey System with Allee Effect on the Prey Species. Mathematics and Computers in Simulation, 94, 33-54. https://doi.org/10.1016/j.matcom.2013.05.009
- 17. Xiao, Z.W. and Li, Z. (2019) Stability and Bifurcation in a Stage-Structured Predator-Prey Model with Allee Effect and Time Delay. International Journal of Applied Mathematics, 49, 1.
- 18. Yang, K., Miao, Z., Chen, F. and Xie, X. (2016) Influence of Single Feedback Control Variable on an Autonomous Holling-II Type Cooperative System. Journal of Mathematical Analysis and Applications, 435, 874-888.
https://doi.org/10.1016/j.jmaa.2015.10.061
- 19. Li, T., Chen, F., Chen, J. and Lin, Q. (2017) Stability of a Stage-Structured Plant-Pollinator Mutualism Model with the Beddington-DeAngelis Functional Response. Journal of Nonlinear Functional Analysis, 2017, Article ID: 50.
https://doi.org/10.23952/jnfa.2017.50
- 20. Sai, A. and Nan, K. (2018) Sparse Grid Interpolation of Ito Stochastic Models in Epidemiology and Systems Biology. IAENG International Journal of Applied Mathematics, 48, 1.
- 21. Wang, L.L. and Xie, P.L. (2017) Permanence and Extinction of Delayed Stage-Structured Predator-Prey System on Time Scales. Engineering Letters, 25, 2.
- 22. Li, Z., Han, M.A. and Chen, F.D. (2012) Global Stability of Stage-Structured Predator-Prey Model with Modified Leslie-Gower and Holling-Type II Schemes. International Journal of Biomathematics, 5, 1250057.
https://doi.org/10.1142/S179352451250057X
- 23. Lin, Y.H., Xie, X.D., Chen, F.D. and Li, T.T. (2016) Convergences of a Stage-Structured Predator-Prey Model with Modified Leslie-Gower and Holling-Type II Schemes. Advances in Difference Equations, 2016, Article No. 181.
https://doi.org/10.1186/s13662-016-0887-2
- 24. Liu, Q., Jiang, D.Q., Hayat, T. and Alsaedi, A. (2018) Dynamics of a Stochastic Predator-Prey Model with Stage Structure for Predator and Holling Type II Functional Response. Journal of Nonlinear Science, 28, 1151-1187.
https://doi.org/10.1007/s00332-018-9444-3
- 25. Liu, M. and Wang, K. (2011) Global Stability of Stage-Structured Predator-Prey Models with Beddington-DeAngelis Functional Response. Communications in Nonlinear Science and Numerical Simulation, 16, 3792-3797.
https://doi.org/10.1016/j.cnsns.2010.12.026
- 26. Zhao, X. and Zeng, Z.J. (2020) Stationary Distribution and Extinction of a Stochastic Ratio-Dependent Predatorprey System with Stage Structure for the Predator. Physica A: Statistical Mechanics and its Applications, 545, 123310.
https://doi.org/10.1016/j.physa.2019.123310
- 27. Mao, X. (1997) Stochastic Differential Equations and Applications. Horwood Publishing, Chichester.
- 28. Has’minskii, R.Z. (1980) Stochastic Stability of Differential Equations. Sijthoff & Noordhoff, Alphen aan den Rijn.
- 29. Wang, H. and Liu, M. (2020) Stationary Distribution of a Stochastic Hybrid Phytoplankton-Zooplankton Model with Toxin-Producing Phytoplankton. Applied Mathematics Letters, 101, 106077.
https://doi.org/10.1016/j.aml.2019.106077
- 30. Liu, Q. and Jiang, D. (2018) Stationary Distribution and Extinction of a Stochastic Predator-Prey Model with Distributed Delay. Applied Mathematics Letters, 78, 79-87. https://doi.org/10.1016/j.aml.2017.11.008
- 31. Lu, C. and Ding, X.H. (2019) Periodic Solutions and Stationary Distribution for a Stochastic Predator-Prey System with Impulsive Perturbations. Applied Mathematics and Computation, 350, 313-322.
https://doi.org/10.1016/j.amc.2019.01.023
- 32. Liu, Q., Jiang, D., Hayat, T. and Alsaedi, T. (2018) Stationary Distribution and Extinction of a Stochastic Predator-Prey Model with Herd Behavior. Journal of the Franklin Institute, 255, 8177-8193.
https://doi.org/10.1016/j.jfranklin.2018.09.013





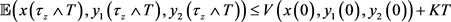 (3.6)
(3.6)