Advances in Applied Mathematics
Vol.
11
No.
12
(
2022
), Article ID:
58789
,
11
pages
10.12677/AAM.2022.1112898
Gamma四元数样条曲线相关问题研究
陈佳惠,王倩*,刘美含,何耀,周奕含
辽宁师范大学数学学院,辽宁 大连
收稿日期:2022年11月5日;录用日期:2022年11月29日;发布日期:2022年12月7日

摘要
随着计算机技术的发展,计算机图形学的重要性逐渐被体现出来,样条曲线也随之迅速发展起来。其研究领域也涉及诸多内容,主要有各阶次样条曲线的不同扩展,光顺的新方法研究以及造型与形状调整。本文将四元数方法与样条理论相结合,以Bézier四元数曲线和Boehm的Gamma样条曲线理论为基础,构建了Gamma四元数样条曲线并对其性质进行研究。首先,将欧氏空间中的Gamma样条曲线推广到四元数空间上,定义了球面Gamma四元数样条曲线。然后,对其光滑性进行了研究,证明了该样条曲线是C1连续的,并且在满足一定条件时,该曲线就是C2连续的。最后,对上述方法进行了应用。该构造方法引入了可以改变样条曲线形状的参数,从而使得构造的样条曲线具有很强的灵活性。
关键词
单位四元数,Bézier四元数曲线,Gamma四元数样条曲线,参数连续

Research on the Correlation Problems of Gamma Quaternion Spline Curves
Jiahui Chen, Qian Wang*, Meihan Liu, Yao He, Yihan Zhou
School of Mathematics, Liaoning Normal University, Dalian Liaoning
Received: Nov. 5th, 2022; accepted: Nov. 29th, 2022; published: Dec. 7th, 2022

ABSTRACT
With the development of computer technology, the importance of computer graphics is gradually reflected, and the spline curve also develops rapidly. Its research field also involves a lot of contents, including different extension of spline curves of various orders, new methods of smoothing and modeling and shape adjustment. Based on Bézier quaternion curve and Boehm’s Gamma spline curve theory, this paper combines quaternion method with spline theory, constructs Gamma quaternion spline curve and studies its properties. Firstly, the Gamma quaternion spline curve in Euclidean space is extended to quaternion space, and the spherical Gamma quaternion spline curve is defined. Then, it is proved that the spline curve is C1 continuous, and it is C2 continuous when certain conditions are satisfied. Finally, the above method is applied. The parameters that can change the shape of the spline curve are introduced in this construction method so that the spline curve can be constructed with strong flexibility.
Keywords:Unit Quaternion, Bézier Quaternion Curve, Gamma Quaternion Spline, Parameter Continuity

Copyright © 2022 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
刚体运动曲线的设计是计算机动画设计中的一个重要问题 [1]。刚体运动通常可以用两种运动的结合来描述:一种是刚体的平移运动,另一种是刚体的旋转运动。在计算机动画中,使用适当的工具来产生刚体平滑和自然运动是非常重要的。而用四元数方法取代欧拉角描述刚体运动的姿态,可以避免大角度旋转时的奇异性,并能完全的描述刚体运动的任何姿态,因此,四元数尤其是单位四元数在虚拟摄像头和三维物体的旋转控制中尤为重要。随着目前空间技术,计算技术,特别是计算机图形学等领域的发展,四元数的优越性又被研究人员重视了起来。
1985年,美国数学家Shoemake [2] 首次将四元数引入到计算机图形学中,并且主要介绍了用Bézier单位四元数曲线来表示刚体的运动。1995年,Kim [3] 等人利用Slerp给出了能够计算一阶导数的单位四元数曲线,并且得到了单位四元数曲线的二阶导数。还利用Bernstein [4] 基函数的累加形式给出了单位四元数的代数方程构造方法,并且首次在论文中给出了Bézier单位四元数曲线,Hermite单位四元数曲线和B-spline单位四元数曲线的代数表达形式。2007年,Ge [5] 等人提出了一种能够插值给定单位四元数序列的 连续B样条四元数曲线的构造方法,虽然同样需要求解非线性方程组,但是能够得到精确的四元数控制点。2017年,邢燕等人 [6] 对单位四元数插值样条曲线的参数二阶连续性与插值性问题进行了研究。为了使产生的四元数曲线连续性更高,2018年邢燕 [7] 将参数二阶连续性提高到了参数三阶连续性,构造了一类基于五次多项式的单位四元数插值样条曲线。檀结庆 [8] 等人提出了具有 连续性的五次多项式单位四元数插值样条曲线,该曲线能够自动插值于给定的数据点。2022年,孙楠等人 [9] 在Kim的基础上对Bézier四元数曲线的性质进行了研究,计算了其端点处的一阶,二阶导矢,解决了曲线的光滑拼接问题,构造出了具有 连续性的四元数插值样条曲线,此方法能够精确地插值于给定的单位四元数序列,并且无需求解非线性方程组。
1987年,Boehm [10] 提出了Gamma样条的概念和构造方法,以两段三次Bézier曲线的拼接为例,从满足 连续条件出发,给出了一组比例约束条件,使得在该约束条件下两段曲线在公共点处满足 连续条件,基于此方法构造出来的 连续组合3次Bézier曲线即为Gamma样条。Gamma样条揭示了 连续样条曲线和B样条曲线的本质联系。1988年,法林 [11] 在Boehm的基础上又给出了满足一定的比例关系,则两三次Bézier曲线段在公共连接点处就是 的。1994年,Sarfraz [12] 采用了一种方法为三次样条曲线构造了B样条曲线的基,并作为一种特殊情况,还可以恢复Gamma样条方法。2011年,Xu [13] 等人提出了一种构造 连续的有理Gamma样条曲线的方法,此方法可以插值给定的一组平面或者空间中不同的有序数据点。
基于以上研究,本文在Boehm的基础上,结合四元数理论,将3维欧式空间 中Gamma样条曲线推广到3维球面 中,构造了Gamma四元数样条曲线,并对其在连接点处的一阶导与二阶导进行了研究。新生成的曲线直接由给定的辅助控制顶点以及形状参数来计算控制顶点,无需求解线性方程组,提高了运算效率。
2. 预备知识
2.1. 四元数
四元数可看作是复数的扩展,其是由1个实数加上3个复数组合而成,通常可以表示为
(或者 ),
其中 , 是三个虚单位,满足 ,,,。
给定两个四元数 ,,令 ,,则相应的运算法则如下 [8]:
四元数的加减定义为
。
四元数的乘法定义为
四元数的共轭定义为
。
四元数的逆定义为
。
给定单位四元数 ,显然 ,令
,
,
那么就得到了单位四元数的一种表示方法 [3]
,
并且
。
对于单位四元数 ,其中 ,,称映射 :
为对数映射 [3],显然
。 (1)
称对数映射的逆映射 :
为指数映射。特别的 。
给定两个单位四元数 和 ,连接 和 的测地线具有恒定的切速度 ,测地线方程为 [4]
。
引理1 [3] 测地线 的一阶导为
。
特别的,当 和 时分别有
,
。
2.2. Bézier四元数曲线
对于 ,用Bernstein基 表示的n阶Bézier曲线如下:
,
其中 是控制点。对于以基形式给出的Bézier曲线,可以将上式转化为累加形式
,
其中 为累加基函数。特别的 。
引理2对于 ,累加基函数 满足:
对于单位四元数 ,利用四元数曲线的构造方法,Kim定义了n次Bézier四元数曲线 [12]
,
其中 。
2.3. Gamma样条曲线
Boehm利用简单的比例仿射概念,直接从一个辅助控制多边形构造出了 连续的三次样条曲线,即Gamma样条曲线 [10]。
对于正整数l,给定一组辅助控制顶点 ,一个节点分割 ,一组形状参数 ,令 ,一条Gamma样条曲线由l段三次Bézier曲线构成。对于 ,每段曲线的内控制顶点定义为 [10]:
对于 ,首末控制顶点定义为 [10]:
特别的,样条曲线的首段控制顶点定义为:
末段控制顶点定义为:
实际上,Gamma样条曲线对于整体参数是 连续的 [14]。特别的,当 时,Gamma样条曲线就退化成了 三次样条曲线。
3. Gamma四元数样条曲线
3.1. Gamma四元数样条曲线的定义
受Kim [4] 的启发,我们将欧式空间 中的Gamma样条曲线推广到单位四元数上,给出了Gamma四元数样条曲线的定义。
给定一组四元数顶点 ,一个均匀的节点分割 和一组形状参数 ,对于 ,Gamma四元数样条曲线 的第i段 定义为
,
其中 ,对于 ,
(2)
(3)
对于 ,
(4)
特别的,对于 ,
对于 ,
称 为辅助控制顶点, 为控制顶点, 为Gamma四元数曲线。由于四元数在三维空间上无法显示,所以我们给出平面上的示意图,如图1所示。
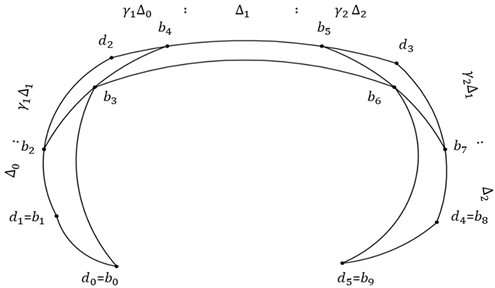
Figure 1. Control point construction diagram
图1. 控制顶点构造示意图
3.2. Gamma四元数样条曲线的性质
我们构造的Gamma四元数样条曲线保持了 中Gamma样条曲线的许多重要微分性质。本节我们要考虑Gamma四元数样条曲线的光滑性。
为了方便起见,对于 ,,令
。
引理3 对于 ,。
i)
ii)
iii)
证明:利用文献4中的结论可得
将 和 分别代入,即可证明引理。
3.2.1. Gamma四元数样条曲线的一阶连续性
定理1 Gamma四元数样条曲线 对于整体参数u是 连续的。
证明:由Gamma四元数曲线的定义及引理3(i)可知,
即曲线是 连续的。
对 求一阶导得
。
由引理2及引理3(i)(ii)可知
,
。
由控制顶点的定义及式(1)得
,
。
由此即可证明定理。
3.2.2. Gamma四元数样条曲线的二阶连续性
二阶导数的不连续性,可能会导致物体最后的旋转结果与期望不符。因此,如何构造具有高阶连续的四元数样条曲线在计算机动画中非常重要。所以在本节中我们给出了Gamma四元数样条曲线 连续的充要条件。
对 求二阶导得
由引理2及引理3可知
,
。
由引理1, 可以转化为
。
由此可得曲线的首末二阶导矢。
定理2 Gamma四元数样条曲线 对于整体参数u是 连续的充要条件
(5)
证明:首先证明必要性。由式(2) (3),可将式(5)转化为
。
由引理1,上式可改写为
。
等式两边同乘 ,整理可得
。
上式两边加 ,由定义即可证明
。
其次证明充分性。令 。由式(4)及定义可将等式转化为
,
由式(1)~(3)经过计算,即可证明等式(5)。
4. 实验
在本节中,我们数值上实现了上述构造Gamma四元数样条曲线的方法。
例1 随机给定球面 上6个辅助控制顶点
令形状参数 ,,利用本文方法,即可构造出由三段曲线组成的Gamma四元数样条曲线。
基于四元数与旋转变换的关系 [15],我们将本文的构造方法应用于刚体旋转运动,其刚体中心点的旋转运动轨迹如图2所示。
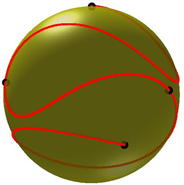
Figure 2. Rotation trajectory of rigid body center point
图2. 刚体中心点旋转运动轨迹
例2 给定球面 上5个辅助控制顶点
令形状参数 ,利用本文的方法,即可计算出Gamma四元数样条曲线的所有控制顶点
通过验证可知这些控制顶点满足式(5),因此样条曲线是 连续的。相应的,我们得到刚体中心点的旋转运动轨迹,如图3所示。
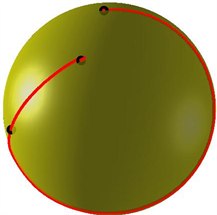
Figure 3. Rotation trajectory of rigid body center point
图3. 刚体中心点的旋转运动轨迹
5. 结论
本文首先将Bézier四元数曲线和Boehm的Gamma样条曲线相结合,构造了Gamma四元数样条曲线,构造的四元数样条曲线不仅是 连续的,并在满足一定条件时是 连续的。本文所构造的四元数样条曲线引入了可以改变样条曲线形状的参数,使得构造的样条曲线形状的改变更具灵活性。在后续的研究中,我们将会对其高阶参数连续以及形状参数对样条曲线形状的影响等问题做进一步展开研究。
文章引用
陈佳惠,王 倩,刘美含,何 耀,周奕含. Gamma四元数样条曲线相关问题研究
Research on the Correlation Problems of Gamma Quaternion Spline Curves[J]. 应用数学进展, 2022, 11(12): 8504-8514. https://doi.org/10.12677/AAM.2022.1112898
参考文献
- 1. Jin, X.G., Bao, H.J. and Peng, Q.S. (1997) A Survey of Computer Animation. Journal of Software, 8, 241-251.
- 2. Shoemake, K. (1985) Animating Rotation with Quaternion Curves. Computer Graphics, 19, 245-254. https://doi.org/10.1145/325165.325242
- 3. Kim, M.J., Kim, M.S. and Shin, S. (1996) A Compact Differential Formula for the First Derivative of a Unit Quaternion Curve. Journal of Vosualization and Computer Animation, 7, 43-57. https://doi.org/10.1002/(SICI)1099-1778(199601)7:1<43::AID-VIS136>3.0.CO;2-T
- 4. Kim, M.J., Kim, M.S. and Shin, S. (1995) A General Construction Scheme for Unit Quaternion Curves with Simple High Order Deraivatives. In: Computer Graphics Proceedings, Annual Conference Series, ACM SIGGRAPH, Los Angeles, 369-376. https://doi.org/10.1145/218380.218486
- 5. Ge, W., Huang, Z. and Wang, G. (2007) Interpolating Solid Orienta-tions with a C2-Continuous B-Spline Quaternion Curve. In: International Conference on Technologies for E-Learning and Digital Entertainment, Springer, Berlin, 606- 615. https://doi.org/10.1007/978-3-540-73011-8_58
- 6. 邢燕, 樊文, 檀结庆, 等. 一类C2连续的单位四元数插值样条曲线[J]. 计算机辅助设计与图形学学报, 2017, 29(1): 45-51.
- 7. 邢燕, 白龙, 樊文, 等. C3连续的单位四元数插值样条曲线[J]. 中国图象图形学报, 2018, 23(4): 534-541.
- 8. Tan, J., Xing, Y., Fan, W., et al. (2018) Smooth Orientation Interpolation Using Parametric Quin-tic-Polynomial-Based Quaternion Spline Curve. Journal of Computational and Applied Mathematics, 329, 256-267. https://doi.org/10.1016/j.cam.2017.07.007
- 9. 孙楠, 王倩, 何耀, 杨雷, 陈佳惠. Bézier四元数曲线相关问题研究[J]. 应用数学进展, 2022, 11(3): 1428-1437.
- 10. Boehm, W. (1987) Smooth Curves and Surfaces. In: Farin, G., Ed., Geometric Modeling: Algorithms and New Trends, SIAM, Philadelphia, 175-184.
- 11. Farin, G. (1990) Curves and Surfaces for Computer Aided Geometric Design. 2nd Edition, Academic Press, Salt Lake City. https://doi.org/10.1016/B978-0-12-460515-2.50020-2
- 12. Muhammad, S. (1994) Cubic Spline Curves with Shape Control. Computers & Graphics, 18, 707-713. https://doi.org/10.1016/0097-8493(94)90165-1
- 13. Xu, C. and Kim, T. (2011) Determining Tension Parameters in Rational Gamma-Spline Interpolation. Applied Mathematics and Computation, 217, 5243-5258. https://doi.org/10.1016/j.amc.2010.11.013
- 14. 施法中. 计算机辅助几何设计与非均匀有理B样条[M]. 修订版. 北京: 高等教育出版社, 2001: 12-24.
- 15. 潘乐. 球面插值样条曲线相关问题研究[D]: [硕士学位论文]. 大连: 辽宁师范大学, 2021.
NOTES
*通讯作者。