设为首页 加入收藏 期刊导航 网站地图

Advances in Applied Mathematics
Vol. 12  No. 07 ( 2023 ), Article ID: 68925 , 11 pages
10.12677/AAM.2023.127320

计算矩阵M-P广义逆的一种迭代法

陈荣

长沙理工大学数学与统计学院，湖南 长沙

收稿日期：2023年6月14日；录用日期：2023年7月9日；发布日期：2023年7月19日

摘要

本文提出了一种求解Moore-Penrose广义逆的高阶迭代法，并证明了该方法具有局部九阶收敛速度。此外，我们进行了数值实验，与已有的迭代法进行计算时间对比，结果表明该方法是有效可行的。

关键词

Moore-Penrose广义逆，迭代法，局部收敛速度

An Iterative Method for Computing Matrix M-P Generalized Inverse

Rong Chen

School of Mathematics and Statistics, Changsha University of Science and Technology, Changsha Hunan

Received: Jun. 14th, 2023; accepted: Jul. 9th, 2023; published: Jul. 19th, 2023

ABSTRACT

In this paper, a high order iterative method for solving the Moore-Penrose generalized inverse is proposed, and it is proved that the method has local ninth order convergence rate. In addition, numerical experiments are carried out to compare the calculation time with the existing iterative methods, and the results show that the proposed method is effective and feasible.

Keywords:Moore-Penrose Generalized Inverse, Iterative Method, Local Convergence Rate

Copyright © 2023 by author(s) and Hans Publishers Inc.

This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).

http://creativecommons.org/licenses/by/4.0/

1. 引言

M-P广义逆在求解线性方程组和线性最小二乘问题具有广泛应用，例如关于求解以下线性方程组：

A x = b , (1.1)

其中 A ∈ C m × n 是系数矩阵，b为已知的m维列向量，x为未知的n维列向量，那么就可以通过计算系数矩阵A的M-P广义逆来求解。关于M-P广义逆的计算，直接法例如奇异值分解法是较为常用的方法，但当A的规模较大时，直接法的计算成本很高，因此，计算M-P广义逆的高效迭代法十分重要。

1906年，Moore [1] 注意到一个矩阵的广义逆的存在性，并且用投影的方式定义每个矩阵的广义逆。1955年，Penrose [2] 以不同的方式重新进行定义，用同时满足四个方程的形式(简称Moore-Penrose方程)，引入唯一的广义逆。下面给出M-P广义逆的定义。

定义设A是复数域上的 m × n 矩阵，若存在一个矩阵 X ∈ C m × n ，使它满足以下Penrose方程：

{ A X A = A , X A X = X , ( A X ) * = A X , ( X A ) * = X A , (1.2)

其中， ∗ 表示矩阵的共轭转置。那么可以证明X是存在且唯一的，X被称为A的M-P广义逆，记作 A † 。

对于许多的数学问题，我们不能通过有限次算术运算及解析方法来求得它的精确解，而只能通过对所求的解进行一次次估计，从而逐步求得它的逼近解，像这种方法我们称为迭代法。一直以来，学者们对于使用迭代法计算广义逆做着许多研究。

学者们不断提出各种估计矩阵M-P逆的方法，大多数这些迭代法都是基于求解以下定义的矩阵方程：

f ( X ) = I − A X = 0. (1.3)

所求出来的矩阵X具有A的逆的部分性质，验证该方法满足M-P逆的定义，则此迭代法可以成为求广义逆的一种迭代法。

1933年，Schulz [3] 提出迭代格式

X k + 1 = X k ( 2 I − A X k ) , k = 0 , 1 , 2 , ⋯ , (1.4)

其中I是 m × m 的单位矩阵， X 0 是矩阵 A − 1 的初始近似，这就是著名的Schulz迭代法，也是计算M-P逆常用的迭代法。该方案完全基于矩阵和矩阵相乘，可以在并行机器上实现。而且如在文献 [4] 中所讨论的，上述方法具有多对数复杂度，并且在数值上是稳定的。

然而，上述方案在开始过程中收敛比较缓慢，导致计算工作量的增加。因此，更高阶的方案被开发出来以降低计算复杂度。例如，W. Li和Z. Li [5] 提出以下三阶迭代方法：

X k + 1 = X k ( 3 I − 3 A X k + ( A X k ) 2 ) , k = 0 , 1 , 2 , ⋯ . (1.5)

2011年，Li等人 [6] 将迭代格式(1.5)改写成以下迭代格式：

X k + 1 = X k ( 3 I − A X k ( 3 I − A X k ) ) , (1.6)

这个也是著名的切比雪夫法。Krishnamurthy和Sen [7] 提出以下的四阶迭代格式：

X k + 1 = X k ( I + Y k ( I + Y k ( I + Y k ) ) ) , (1.7)

其中 Y k = I − A X k 。

Soleymani [8] 中提出了以下五阶迭代格式，每次迭代需要六次矩阵相乘：

X k + 1 = − 1 2 X k ( − 11 I + A X k ( 25 I + A X k ( − 30 I + A X k ( 20 I + A X k ( − 7 I + A X k ) ) ) ) ) . (1.8)

Soleymani [9] 等人引入以下六阶方法，每次迭代使用五次矩阵和矩阵相乘：

{ B k = A X k , C k = B k ( − I + B k ) , X k + 1 = X k ( 2 I − B k ) ( 3 I − 2 B k + C k ) ( I + C k ) . (1.9)

2012年，Soleymani [10] 又开发七阶迭代方案，每次迭代需要八次矩阵相乘：

X k + 1 = 1 16 X k [ 120 I + A X k ( − 393 I + A X k ( 735 I + A X k ( − 861 I + A X k ( 651 I           + A X k ( − 315 I + A X k ( 93 I + A X k ( − 15 I + A X k ) ) ) ) ) ) ) ] . (1.10)

1986年，Krishnamurthy和Sen [7] 提出这类Schulz型迭代方案的一般形式。2013年，Li [11] 等人对这类迭代方案进行理论研究，证明Schulz型矩阵迭代法在数值上是稳定的。通过这种方法，提出每个基于超幂级数的p阶迭代方法，每次迭代需要p次矩阵和矩阵乘法。例如，需要九个矩阵和矩阵乘法的九阶迭代方案定义如下：

X k + 1 = X k [ I + Y k ( I + Y k ( I + Y k ( I + Y k ( I + Y k ( I + Y k ( I + Y k ( I + Y k ) ) ) ) ) ) ) ] , (1.11)

其中 Y k = I − A X k 。

本文构造一种新的高阶迭代方法来逼近M-P逆。首先，从理论上证明提出的方案对非奇异矩阵收敛于九阶。之后，我们研究生成的迭代序列到M-P逆的收敛性。通过计算效率，我们将该迭代方案与先前的迭代方案进行理论比较。最后进行数值实验，对于要求广义逆的给定矩阵A，我们的迭代方案所需迭代次数与迭代时间与原有的迭代格式进行对比，验证该方案是有效可行的。

2. 算法

在本节中，我们构造一种新的求矩阵广义逆的迭代方法。为此，我们考虑以下新的有理迭代函数：

{ Y k = X k − F ( X k ) 2 F ′ ( X k ) ( 2 + F ″ ( X k ) F ( X k ) F ′ ( X k ) 2 ) , Z k = Y k − F ( Y k ) F ′ ( Y k ) , X k + 1 = Y k − ( F ( Y k ) − 1 5 F ( Z k ) F ′ ( Z k ) ) ( 1 − 4 5 F ( Z k ) F ( Y k ) ) , k = 0 , 1 , 2 , ⋯ , (2.1)

注意到，(2.1)在求解非线性方程的零点时具有局部九阶收敛性。

现在，为了计算给定矩阵A的逆，将迭代方案(2.1)应用于矩阵函数(1.3)，得到以下迭代格式：

X k + 1 = − 1 25 X k ( 3 I + A X k ( − 3 I + A X k ) ) ( − 79 I + A X k ( 3 I + A X k ( − 3 I + A X k ) )                     × ( 87 I + A X k ( 3 I + A X k ( − 3 I + A X k ) ) ( − 37 I + 4 A X k ( 3 I + A X k ( − 3 I + A X k ) ) ) ) )                 = 1 25 X k [ 237 I − 1020 A X k + 2644 ( A X k ) 2 − 4626 ( A X k ) 3 + 5814 ( A X k ) 4                     − 5460 ( A X k ) 5 + 3924 ( A X k ) 6 − 2169 ( A X k ) 7 + 901 ( A X k ) 8                     − 264 ( A X k ) 9 + 48 ( A X k ) 10 − 4 ( A X k ) 11 ] ,     k = 0 , 1 , 2 , ⋯ .

在上述的等式中，矩阵和矩阵相乘的次数是十二，这增加了每次迭代的计算量。而通过适当的因子分解技术，可以使计算成本最小化，从而提高计算效率。为此，将上式改写成以下矩阵迭代格式：

{ B k = A X k , C k = 3 I + B k ( − 3 I + B k ) , S k = B k C k , X k + 1 = − 1 25 X k C k ( − 79 I + S k ( 87 I + S k ( − 37 I + 4 S k ) ) ) , k = 0 , 1 , 2 , ⋯ . (2.2)

在上述简化形式(2.2)中，每次迭代时的矩阵相乘减少到七次。此外，该迭代格式(2.2)也属于Schulz型方法。在下一节中，我们将陈述并证明该方案在某些假设下具有九阶收敛性。

3. 理论分析

本节针对提出的迭代格式(2.2)，分别讨论其对于非奇异复矩阵以及一般复矩阵的收敛性分析。

3.1. 收敛性分析

定理3.1假设A是一个 n × n 阶非奇异复矩阵。如果初始迭代矩阵 X 0 满足以下条件：

‖ I − A X 0 ‖ < 1 , (3.1)

那么迭代格式(2.2)九阶收敛于 A † 。

证明：假设不等式(3.1)成立，设 E k = I − A X k 为每步迭代的残差矩阵，那么 E 0 = I − A X 0 为初始残差矩阵。我们可以得到第k + 1步残差矩阵为：

E k + 1 = I − A X k + 1 = I − 1 25 [ 237 A X k − 1020 ( A X k ) 2 + 2644 ( A X k ) 3 − 4626 ( A X k ) 4     + 5814 ( A X k ) 5 − 5460 ( A X k ) 6 + 3924 ( A X k ) 7 − 2169 ( A X k ) 8     + 901 ( A X k ) 9 − 264 ( A X k ) 10 + 48 ( A X k ) 11 − 4 ( A X k ) 12 ]

= 1 25 ( − I + A X k ) 9 ( − 25 I + 4 A X k ( 3 I + A X k ( − 3 I + A X k ) ) ) = 1 25 ( I − A X k ) 9 ( 21 I + 4 ( I − A X k ) 3 ) = 1 25 E k 9 ( 21 I + 4 E k 3 ) .

在等式两边取矩阵范数得：

‖ E k + 1 ‖ ≤ ‖ 1 25 E k 9 ( 21 I + 4 E k 3 ) ‖ = 1 25 [ 21 ‖ E k ‖ 9 + 4 ‖ E k ‖ 12 ] . (3.2)

接下来我们使用数学归纳法，由假设条件(3.1)知 ‖ E 0 ‖ < 1 ，代入(3.2)得到：

‖ E 1 ‖ ≤ 1 25 [ 21 ‖ E 0 ‖ 9 + 4 ‖ E 0 ‖ 12 ] < 1.

现在，我们假设 ‖ E k ‖ < 1 ，那么

‖ E k + 1 ‖ ≤ 1 25 [ 21 ‖ E k ‖ 9 + 4 ‖ E k ‖ 12 ] ≤ ‖ E k ‖ 9 .

然后，我们可以得到

‖ E k + 1 ‖ ≤ ‖ E k ‖ 9 ≤ ⋯ ≤ ‖ E 0 ‖ 9 k + 1 < 1.

因此，当 k → ∞ 时， I − A X k → 0 ，也就是说当 k → ∞ 时， X k → A − 1 。

现在我们证明了在假设(3.1)成立的情况下，由迭代格式(2.2)生成的矩阵序列 { X k } k = 0 k = ∞ 收敛于矩阵 A − 1 。接下来，我们证明该序列的收敛阶数至少为九阶。为此，我们将第k步迭代的误差矩阵定义为：

ε k = A − 1 − X k ,

那么就有 A ε k = I − A X k = E k 。因此在第k+1步迭代时有：

A ε k + 1 = E k + 1 = 1 25 E k 9 ( 21 I + 4 E k 3 ) = 1 25 [ 21 ( A ε k ) 9 + 4 ( A ε k ) 12 ] .

由于A是可逆的，由上式可得：

ε k + 1 = 1 25 [ 21 ε k ( A ε k ) 8 + 4 ε k ( A ε k ) 11 ] .

对两边取矩阵范数，我们可以得到：

‖ ε k + 1 ‖ ≤ ( 1 25 [ 21 ‖ A ‖ 8 + 4 ‖ A ‖ 11 ‖ ε k ‖ 3 ) ‖ ε k ‖ 9 .

不等式表明，在假设条件(3.1)成立的情况下，由迭代格式(2.2)生成的矩阵序列 { X k } k = 0 k = ∞ 至少以九阶收敛于 A − 1 ，证毕。

在定理3.1中分析，一定条件下，新构造的迭代方法(2.2)对于非奇异复矩阵是收敛的。因此，初始迭代矩阵 X 0 对该方法的收敛性起着重要的作用。

Pan和Schreiber提出，可以选择

X 0 = α A * , (3.3)

作为初始迭代矩阵，其中 α 是一个足够小的正数， A * 是给定矩阵A的共轭转置矩阵。式(3.3)中 α 的最优选择是 2 σ 1 2 + σ r 2 ，其中 σ 1 = ‖ A ‖ 2 ， σ r = 1 ‖ A † ‖ 2 。然而， σ r 较难获得，但是我们可以知道

σ min ≤ σ 1 2 ≤ σ r 2 ≤ σ max ,

其中， σ min 和 σ max 分别是矩阵A的奇异值的上界和下界。根据上述不等式，可以得到最优一般初始选择：

X 0 = 2 σ min 2 + σ max 2 A * .

除此之外，Pan和Schreiber还提出了 α 的次优值为

α = 1 ‖ A ‖ 1 ‖ A ‖ ∞ .

另外地，对于不同类型的矩阵，可以选取不同的初始矩阵，可见文献 [12] 。

3.2. Moore-Penrose广义逆的收敛性

本小节讨论当矩阵A为任意 m × n 阶复矩阵时，上述所提出的迭代方案对Moore-Penrose逆的收敛性，我们还将证明它的收敛速度保持不变。接下来，用引理说明所提出的方案满足Penrose方程。

引理3.2对于由迭代格式(2.2)以及初始矩阵 X 0 = α A * 生成的矩阵迭代序列 { X k } k = 0 k = ∞ ，以下矩阵方程组

成立：

{ ( a )     X k A A † = X k , ( b )     A † A X k = X k , ( c )     ( A X k ) * = A X k , ( d )     ( X k A ) * = X k A .

证明：使用数学归纳法证明引理。对于等式(a)，我们首先证明 k = 0 时，等式成立：

X 0 A A † = α A * A A † = α A * ( A A † ) * = α A * ( A † ) * A * = α ( A A † A ) * = α A * = X 0 .

假设当 k = n ，等式(a)成立，即 X n A A † = X n 。那么我们要证明当 k = n + 1 时，等式(a)成立，即 X n + 1 A A † = X n + 1 。使用迭代格式(2.2)，我们得到：

X n + 1 A A † = 1 25 X n [ 237 I − 1020 A X n + 2644 ( A X n ) 2 − 4626 ( A X n ) 3 + 5814 ( A X n ) 4     − 5460 ( A X n ) 5 + 3924 ( A X n ) 6 − 2169 ( A X n ) 7 + 901 ( A X n ) 8 − 264 ( A X n ) 9     + 48 ( A X n ) 10 − 4 ( A X n ) 11 ] A A †

= 1 25 [ 237 X n A A † − 1020 X n A X n A A † + 2644 X n A X n ( A X n A A † ) − 4626 X n ( A X n ) 2 ( A X n A A † )     + 5814 X n ( A X n ) 3 ( A X n A A † ) − 5460 X n ( A X n ) 4 ( A X n A A † ) + 3924 X n ( A X n ) 5 ( A X n A A † )     − 2169 X n ( A X n ) 6 ( A X n A A † ) + 901 X n ( A X n ) 7 ( A X n A A † ) − 264 X n ( A X n ) 8 ( A X n A A † )     + 48 X n ( A X n ) 9 ( A X n A A † ) − 4 X n ( A X n ) 10 ( A X n A A † ) ] .

由已知得 X n A A † = X n ，将其代入上式可得：

X n + 1 A A † = 1 25 [ 237 X n − 1020 X n A X n + 2644 X n ( A X n ) 2 − 4626 X n ( A X n ) 3     + 5814 X n ( A X n ) 4 − 5460 X n ( A X n ) 5 + 3924 X n ( A X n ) 6 − 2169 X n ( A X n ) 7     + 901 X n ( A X n ) 8 − 264 X n ( A X n ) 9 + 48 X n ( A X n ) 10 − 4 X n ( A X n ) 11 ] = X n .

因此，由数学归纳法，对于任意 k ∈ N ，条件(a)得证。

对于第三个条件等式(c)，首先，我们验证当 k = 0 时，等式(c)成立：

( A X 0 ) * = ( A α A * ) * = α ( A * ) * A * = α A A * = A α A * = A X 0 .

假设当 k = n ，等式(c)成立，即 ( A X n ) * = A X n 。那么我们要证明当 k = n + 1 时，等式(c)成立，即 ( A X n + 1 ) * = A X n + 1 。因此，使用迭代格式(2.2)，我们得到：

( A X n + 1 ) * = 1 25 [ 237 ( A X k ) * − 1020 ( ( A X k ) 2 ) * + 2644 ( ( A X k ) 3 ) * − 4626 ( ( A X k ) 4 ) *       + 5814 ( ( A X k ) 5 ) * − 5460 ( ( A X k ) 6 ) * + 3924 ( ( A X k ) 7 ) * − 2169 ( ( A X k ) 8 ) *       + 901 ( ( A X k ) 9 ) * − 264 ( ( A X k ) 10 ) * + 48 ( ( A X k ) 11 ) * − 4 ( ( A X k ) 12 ) * ] .

由已知得 ( A X n + 1 ) * = A X n + 1 成立，那么上式可以写成：

( A X n + 1 ) * = 1 25 [ 237 A X k − 1020 ( A X k ) 2 + 2644 ( A X k ) 3 − 4626 ( A X k ) 4     + 5814 ( A X k ) 5 − 5460 ( A X k ) 6 + 3924 ( A X k ) 7 − 2169 ( A X k ) 8 ] .

因此，由数学归纳法，对于任意 k ∈ N ，条件(c)得证。同样地，条件(b)和条件(d)也可以类似地证明。综上所述，引理得证。

在下一个定理中，我们将证明迭代格式(2.2)对于M-P逆的收敛速度。

引理3.3对于任意给定的复矩阵A，由迭代格式(2.2)以及初始矩阵 X 0 = α A * 生成矩阵迭代序列 { X k } k = 0 k = ∞ ，该序列以九阶收敛于给定矩阵的M-P逆 A † 。

证明：我们设 E k = X k − A † ，把它作为用迭代格式(2.2)逼近M-P逆时第k步的误差矩阵。那么我们可以得到：

A E k + 1 = A X k + 1 − A A † = A X k + 1 − I + I − A A † = − E k + 1 + I − A A † = 1 25 ( 21 E k 9 + 4 E k 12 ) + I − A A † .

我们可以证明 ( I − A A † ) t = I − A A † , t ∈ N ，以及 ( I − A A † ) A E k = 0 ，把它们代入上式得到：

A E k + 1 = 1 25 ( 21 ( A E k ) 9 − 4 ( A E k ) 12 ) . (3.4)

设 P = A A † 以及 S = I − A X 0 ，那么有 P 2 = P ，还得到：

P S = A A † ( I − A X 0 ) = A A † − A A † A X 0 = A A † − A X 0 = A A † − A X 0 A A † = ( I − A X 0 ) A A † = S P .

另外，Stanimirović和Cvetković-llić表明，若存在 P ∈ ℂ n × n 和 S ∈ ℂ n × n ，使得 P = P 2 和 P S = S P 成立，那么有 ρ ( P S ) ≤ ρ ( S ) 。因此，我们可以得到：

ρ ( A ( X 0 − A † ) ) = ρ ( A ( α A ∗ − A † ) ) ≤ ρ ( I − α A A ∗ ) = max 1 ≤ i ≤ r | 1 − λ i ( α A A ∗ ) | < 1 ,

其中，r为奇异值的个数， ρ 为矩阵的谱半径。我们知道，存在一个正常数 ϵ 和一个矩阵范数 ‖   ⋅   ‖ ，使得：

A ( X 0 − A † ) ≤ ρ ( A ( X 0 − A † ) ) + ϵ < 1 ,

这也意味着 ‖ A E 0 ‖ < 1 。此外，对(3.4)两边同时使用矩阵范数可得：

‖ A E k + 1 ‖ ≤ 1 25 [ 21 ‖ A E k ‖ 9 + 4 ‖ A E k ‖ 12 ] ≤ ‖ A E k ‖ 9 ≤ ‖ A ‖ 9 ‖ E k ‖ 9 . (3.5)

现在，我们提出的迭代格式(2.2)在计算M-P逆时的误差为：

‖ X k + 1 − A † ‖ = ‖ A † A X k + 1 − A † A A † ‖ ≤ ‖ A † ‖ ‖ A X k + 1 − A A † ‖ = ‖ A † ‖ ‖ A ‖ ‖ E k + 1 ‖ .

将不等式(3.5)代入到上式中，可以得到：

‖ E k + 1 ‖ = ‖ X k + 1 − A ‖ † ≤ ‖ A ‖ † ‖ A ‖ 9 ‖ E k ‖ 9 . (3.6)

因此，当 k → ∞ 时， ‖ X k + 1 − A † ‖ → 0 。因此，(3.6)证明由迭代格式(2.2)生成的矩阵序列 { X k } k = 0 k = ∞ 在假

设条件下，至少以九阶收敛于给定矩阵A的M-P广义逆。证毕。

3.3. 计算效率

如第1节所述，高阶求矩阵广义逆的最一般的方法是利用p次矩阵和矩阵相乘构造局部p阶矩阵迭代，而本文构造的方法(2.2)仅需要使用七次矩阵相乘便具有局部九阶收敛性。Traub将p阶迭代方法的计算效率指数(CEI)定义为：

C E I = p 1 θ ,

其中 θ 表示算法总的计算成本。每个Schulz型迭代方法的计算成本都由矩阵和矩阵相乘控制，让我们假设每次矩阵相乘的成本是统一的。那么对于每次迭代需要 μ 次矩阵相乘，迭代次数为S的迭代算法，其计算成本为 θ = μ S ，Soleymani [8] 提出p阶Schulz型迭代方法大约需要以下迭代次数：

S = 2 log p κ 2 ( A ) ,

其中 κ 2 是给定矩阵在 ‖   ⋅   ‖ 2 下的条件数。因此，p阶迭代方法的计算效率指数为：

C E I = p 1 μ ( 2 log p κ 2 ( A ) ) . (3.7)

利用计算效率指数这一概念，我们将迭代格式(1.4)、(1.6)、(1.8)、(1.9)、(1.10)、(1.11)与新构造格式(2.2)进行比较。分别用1、2、3、4、5、6以及new代表上述格式，由图1可以看出，在不同的条件数下，我们提出的方法都具有较高的计算效率。

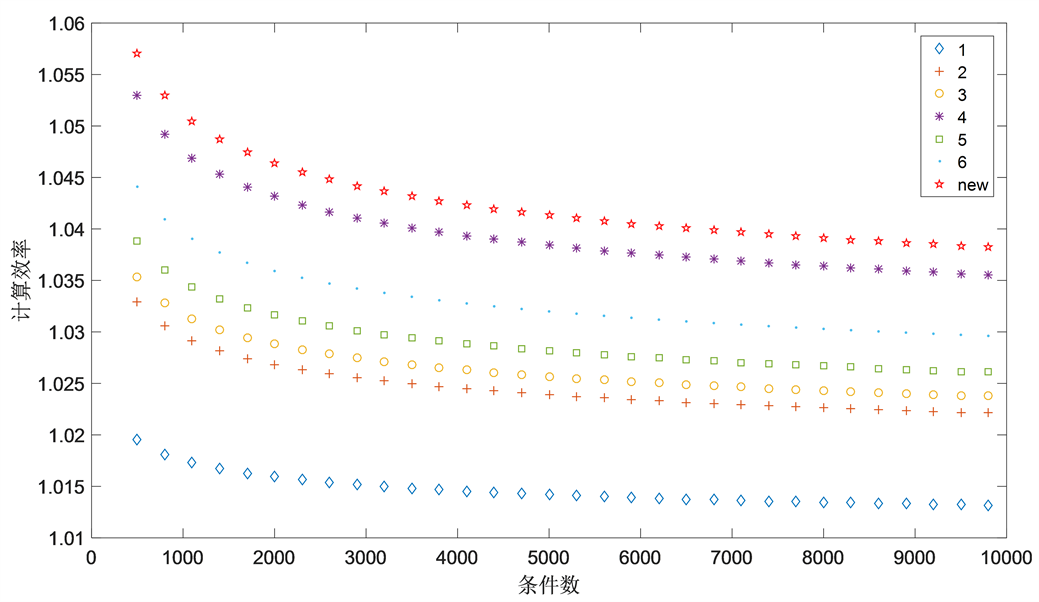
Figure 1. Comparison of calculation efficiency of different methods

图1. 不同方法计算效率比较

因此，新构造的方法从效率上来说是理论有效的。

4. 数值实验

本节给出构造格式(2.2)的数值实验结果，并且与迭代格式(1.4)、(1.6)、(1.8)、(1.9)、(1.10)、(1.11)进行比较，主要进行迭代次数与迭代时间的对比，展现此迭代格式的优势。算法在MATLABR2016a编程实现，数值实验在PC机上Windows系统中进行。

在本节中选择初始迭代矩阵为 X 0 = 2 σ min 2 + σ max 2 A * ，终止条件为 ‖ X k + 1 − X k ‖ < ε [13] ，数值实验每次

进行多次实验取平均值。数值实验如下：

例4.1 考虑如下5阶病态Hilbert矩阵(文献 [14] 中例1)

A = [ 1 1 2 1 3 1 4 1 5 1 2 1 3 1 4 1 5 1 6 1 3 1 4 1 5 1 6 1 7 1 4 1 5 1 6 1 7 1 8 1 5 1 6 1 7 1 8 1 9 ] .

数值实验结果如表1所示，其中迭代格式(1.10)不收敛，迭代格式(2.2)平均迭代次数最小，需要25次，平均时间也为最少。

Table 1. Example 4.1 experimental comparison

表1. 例4.1实验对比

例4.2 考虑如下5阶秩亏矩阵(文献 [15] 中例4)

A = [ 0 0 0 2 0 4 1 0 2 0 0 − 2 0 1 0 0 0 0 2 0 2 1 4 − 3 1 ]

数值实验结果如表2所示，其中迭代格式(2.2)平均迭代次数最小，需要29次，平均时间也为最少。

Table 2. Example 4.2 experimental comparison

表2. 例4.2实验对比

例4.3 考虑随机 n × ( n + 20 ) 阶矩阵( n = 200 )

数值实验结果如表3所示，其中迭代格式(2.2)平均迭代次数最小，需要9次，平均时间也为最少。

Table 3. Example 4.3 experimental comparison

表3. 例4.3实验对比

从以上数值例子可以看出，迭代格式(2.2)所使用的平均迭代次数和平均使用时间都是最少的，因此该算法是有效可行的。

5. 结论

本文构造了一种计算给定复矩阵的M-P逆的高阶迭代方案。在一定条件下，该方法至少能达到九阶收敛性。理论分析表明，该方案采用了较小的矩阵相乘数，从而提高其计算效率指标。图1表明，相对于现有的迭代方法，该方法有着较高的计算效率指标。数值实验结果表明，该方案在较小的计算时间内准确地得到期望的结果。因此，研究结果支持并证明所提出的方法的有效性。

文章引用

陈 荣. 计算矩阵M-P广义逆的一种迭代法
An Iterative Method for Computing Matrix M-P Generalized Inverse[J]. 应用数学进展, 2023, 12(07): 3200-3210. https://doi.org/10.12677/AAM.2023.127320

参考文献

  1. 1. Moore, E.H. (1920) On the Reciprocal of the General Algebraic Matrix. Bulletin of the American Mathematical Society, 26, 394-395. https://doi.org/10.1090/S0002-9904-1920-03332-X

  2. 2. Penrose, R. (1955) A Generalized Inverse for Matrices. Mathematical Proceedings of the Cambridge Philosophical Society, 51, 406-413. https://doi.org/10.1017/S0305004100030401

  3. 3. Schulz, G. (1933) Iterative Berechung der reziproken Matrix. Journal of Applied Mathematics and Mechanics, 13, 57-59. https://doi.org/10.1002/zamm.19330130111

  4. 4. Penrose, R. (1956) On Best Approximate Solutions of Linear Matrix Equations. Mathematical Proceedings of the Cambridge Philosophical Society, 52, 17-19. https://doi.org/10.1017/S0305004100030929

  5. 5. Li, W.G. and Li, Z. (2010) A Family of Iterative Methods for Computing the Approximate Inverse of a Square Matrix and Inner Inverse of a Non-Square Matrix. Applied Mathematics and Computation, 215, 3433-3442. https://doi.org/10.1016/j.amc.2009.10.038

  6. 6. Li, H.B., Huang, T.Z., Zhang, Y., Liu, X.P. and Gu, T.X. (2011) Chebyshev-Type Methods and Preconditioning Techniques. Applied Mathematics and Computation, 218, 260-270. https://doi.org/10.1016/j.amc.2011.05.036

  7. 7. Krishnamurthy, E.V. (1986) Numerical Algorithms: Computations in Science and Engineering. Affiliated East-West Press, New Delhi.

  8. 8. Soleymani, F. (2014) On Finding Robust Ap-proximate Inverses for Large Sparse Matrices. Linear and Multilinear Algebra, 62, 1314-1334. https://doi.org/10.1080/03081087.2013.825910

  9. 9. Soleymani, F., Stanimirović, P.S. and Ullah, M.Z. (2013) An Accelerated Iterative Method for Computing Weighted Moore—Penrose Inverse. Applied Mathematics and Computation, 222, 365-371. https://doi.org/10.1016/j.amc.2013.07.039

  10. 10. Soleymani, F. (2012) A Rapid Numerical Algorithm to Compute Matrix Inversion. International Journal of Mathematics and Mathematical Sciences, 2012, Article ID: 134653. https://doi.org/10.1155/2012/134653

  11. 11. Weiguo, L., Juan, L. and Tiantian, Q. (2013) A Family of Iterative Methods for Computing Moore—Penrose Inverse of a Matrix. Linear Algebra and Its Applications, 438, 47-56. https://doi.org/10.1016/j.laa.2012.08.004

  12. 12. Pan, V.Y. (2010) Newton’s Iteration for Matrix Inversion, Advances and Extensions. In: Olshevsky, V. and Tyrtyshnikov, E., Eds., Matrix Methods: Theory, Algorithms and Applications, Imperial College Press, London, 364-381. https://doi.org/10.1142/9789812836021_0024

  13. 13. Wei, Y.M. (2000) Successive Matrix Squaring Algorithm for Computing the Drazin Inverse. Applied Mathematics and Computation, 108, 67-75. https://doi.org/10.1016/S0096-3003(98)10118-2

  14. 14. Iram, Z.A. and Zein, A. (2022) A New Family of Sec-ond-Order Iterative Methods for Computing the Moore Penrose Inverse Based on Penrose Equations. International Journal of Applied Mathematics, 35, 365-380. https://doi.org/10.12732/ijam.v35i3.1

  15. 15. Kaur, M., Kansal, M. and Kumar, S. (2021) An Efficient Matrix Iterative Method for Computing Moore—Penrose Inverse. Mediterranean Journal of Mathematics, 18, Article No. 42. https://doi.org/10.1007/s00009-020-01675-4

期刊菜单