ABSTRACT

Firstly, seven methods are discussed exhaustively for the variable structure control singular systems with time-delays, including the method of sliding mode approximation, the method of soft variable structure control, restricted synthesis method, the method of adaptive sliding mode control and others. Secondly, so far some research advances in this system are summarized. Finally, some new research directions for relevant variable structure control singular systems with time delays are pointed out.

Keywords:Time-Delay, Singular System, Variable Structure Control, Method of Sliding Mode Control

时滞广义变结构控制研究新进展

张利¹，高存臣^1*，刘云龙²

¹中国海洋大学数学科学学院，山东 青岛

²潍坊学院信息与控制工程学院，山东 潍坊

收稿日期：2018年10月4日；录用日期：2018年10月22日；发布日期：2018年10月29日

摘 要

详细地论述了包括滑模近似法、软变结构控制法、受限综合法、自适应滑模控制法等共七种常用的时滞广义变结构控制方法；总结了到目前为止，国内外学者对该类控制系统的若干研究进展；最后提出了几个关于时滞广义变结构控制系统的新的研究方向。

关键词 :时滞，广义系统，变结构控制，滑模控制法

Copyright © 2018 by authors and Hans Publishers Inc.

This work is licensed under the Creative Commons Attribution International License (CC BY).

http://creativecommons.org/licenses/by/4.0/

1. 引言

随着科学技术的发展和计算机技术的不断增强，研究者们对于实际控制系统的描述渐渐从传统的数学模型转向非传统的数学模型。如在经济学中，控制系统的状态变量所需要满足的状态方程既含有微分方程，又含有差分方程，在数学中这类系统称之为广义系统(singular system)。广义系统是适用性更广泛的一类动态系统，它能够将若干个正常系统所无法描述的系统性能特征给描述出来。因此，广义系统及其特性在研究与应用领域中引起了国内外众多研究学者的极大关注，并在控制理论研究领域中占有重要的地位。随着现代控制理论在工程领域中的不断发展，在能源、电力、生态与经济等其他学科的不断研究，出现了越来越多的大型动力系统。通常，这类大系统可分解为若干子系统，且每个子系统都有其各自的动态性能，同时各子系统之间又是彼此联系和互相制约，关于大系统的性质与应用研究已经出现了若干研究成果 [1] ，但是，对大系统利用滑模控制法进行研究还是近几年的事情。给出如下控制系统：

$\{\begin{array}{c}E\left(x,t\right)\stackrel{\dot{}}{x}=f\left(x,u,t\right)\\ y=g\left(x,u,t\right)\end{array}$ (1)

其中 $x\in {ℝ}^n$ 为系统状态向量， $u\in {ℝ}^r$ 为系统控制输入向量， $y\in {ℝ}^m$ 为系统输出向量， $f,g$ 为 $x,u,t$ 的向量函数， $E\left(x,t\right)\in {ℝ}^{n\times n}$ 为函数矩阵。当 $\text{rank}E=n$ 时，式(1)为正常系统；当 $\text{rank}E=r<n$ 时，称式(1)为广义系统。

广义系统在不同的学科研究领域中具有不同的科学术语，如在数学物理科学领域中称之为“隐式系统” [2] [3] ，在工程经济学领域中称之为“描述器系统” [4] [5] ，在数值分析领域中称之为“微分代数系统” [6] 等等。随着对广义系统的深入研究，广义系统的理论和应用研究领域不断扩大。其中，Zhang等在非线性奇异系统 [7] 的研究中，提出了一种新的非线性滑动面，研究了非线性奇异系统的滑模控制问题；在离散时滞广义系统 [8] 中研究了一类具有状态时滞和参数不确定性的离散广义系统的时滞相关非脆弱鲁棒 $H_{\infty }$ 控制问题；在奇异随机马尔可夫跳跃系统 [9] [10] [11] 中，分别研究了不确定性的奇异随机马尔可夫跳变系统的滑模控制设计问题，利用T-S模糊技术研究了非线性奇异半马尔可夫跳跃系统的滑模控制以及具有时变时滞和执行器饱和的离散时间奇异马尔可夫跳变系统的基于鲁棒观测器的有限时间 $H_{\infty }$ 控制问题。以上对于广义系统的研究，极大地丰富了广义系统理论，拓宽了研究领域。此外广义系统在航空航天、海洋探测等众多应用领域中都有重要的应用背景与理论价值，如受限机器人模型 [12] ，石油的催化裂化过程 [13] ，卫星模型 [14] ，复杂电路系统 [15] [16] [17] 等等。

2. 变结构控制与广义系统概述

2.1. 变结构概述

变结构控制(variable structure control, VSC)理论是现代控制理论研究当中的一个重要方法，是研究非线性控制的一种有效方法，通过对控制器的结构的调整，使得该系统的动态性能得以提升，同时具有响应速度快，抗干扰能力强，调节精度高等优势，其主要控制模式可大致分为三类：1) 滑模控制；2) 切换监督控制；3) 无滑模变结构控制。

随着现代计算机技术的不断发展，众多国内外优秀学者对变结构控制理论研究也在不断完善扩展。对于滑模变结构控制，Shen [18] ，Gao [19] 对于自适应滑模控制进行了研究；研究领域进行扩展，Gao [20] - [27] 等在鲁棒滑模控制，奇异马尔可夫跳变系统的滑模控制，时滞系统滑模控制，积分滑模控制等领域内研究成果丰富，是对滑模控制的理论体系进行扩展渗透；以及Yunlong Liu [28] 等将滑动模控制运用到神经网络系统中，及Delta算子不确定系统的滑模控制研究 [29] 。将滑模控制的应用到不同的系统当中，而对于软变结构控制研究过程中，Gao，Liu等提出了一种控制策略：基于隐Lyapunov函数的变结构控制 [30] ；并且针对广义系统的抖振问题，给出一种新的控制策略：软变结构控制法 [31] ；而对于水下机器人滑模变结构抖振问题，利用具有光滑性和饱和性的sigmoid函数，设计出水下机器人软变结构控制策略 [32] 。在以上的研究成果中极大丰富了变结构控制的理论和应用领域。对于变结构控制在其他领域的研究成果也颇多，如Sun [33] 等基于变结构控制理论方法，研究了一类布尔网络镇定性问题；Wang [34] ，Huang [35] ，Yang [36] ，Chen [37] ，Wang [38] 等人将控制系统扩展到分数阶系统，在分数阶系统中继续研究滑模控制，拓展了新的研究领域，也丰富了变结构控制的理论体系；Zheng [39] 等研究了具有参数不确定性和风干扰的机器人飞艇自适应滑模轨迹跟踪控制；Kang [40] 等基于改进GMS摩擦模型的电液负载模拟器研究了有限时间自适应滑模控制问题等等，这些研究成果极大地丰富了变结构控制理论体系，使得滑模控制设计方法得到了很好的完善与补充。

2.2. 广义系统概述

自20世纪80年代以来，广义系统的理论研究已经深入到控制理论研究中，由于广义系统具有许多区别于常规系统的若干本质特性，所以广义系统对实际模型的描述更加贴合实际。近年来，广义系统的变结构控制问题也引起了诸多国内外学者的重视，在其理论与应用研究领域中不断有新成果出现。如Long [41] 研究了一类中立型变时滞广义系统的稳定性分析；将系统推广到分数阶系统，Dassios [42] 研究了广义系统中的Caputo及其相关分数阶导数，将研究领域进行了扩展；Tudor [43] 等利用Riccati方程，研究了一类广义离散系统的鲁棒镇定问题，最后给出了最大可达稳定裕度和鲁棒镇定控制器；Tsai [44] 等针对具有匹配或者不匹配扰动的广义连续时间混沌系统，提出了一种具有鲁棒抑制的离散滑模控制器；Cui [45] 等通过引入辅助系统，研究了具有分布时滞的连续时间正奇异系统的稳定性分析问题，最后给出了具有分布滞后的奇异系统的充要条件；Zhang [46] 等研究了一类分数阶线性广义系统的鲁棒稳定性及可容许性问题；Ma [47] 等基于鲁棒观测器，研究了一类具有时变时滞和执行器饱和的离散时间奇异马尔可夫跳变系统的有限时间 $H_{\infty }$ 控制问题；因此对于时滞广义系统的理论研究尤为必要，这也是国内外学者研究的前沿课题之一。

3. 时滞广义变结构控制系统研究方法

随着对时滞广义系统的不断深入研究和发展，共有以下七种方法在时滞广义系统的研究领域中占有重要的地位，分别是：滑模近似法、受限综合法、软变结构控制法、趋近律法、受限等价法、自适应滑模控制法和随机广义控制法。下面分述这些研究方法。

3.1. 滑模近似法

考虑如下系统：

$\{\begin{array}{l}E\stackrel{\dot{}}{x}\left(t\right)=\left(A+\text{Δ}A\right)x\left(t\right)+\left(B+\text{Δ}B\right)x\left(t-\tau \right)+\left(F+\text{Δ}F\right)u\left(t\right)+Dg\left(t\right)\\ x\left(t\right)=\phi \left(t\right),t\in \left[-\tau ,0\right]\end{array}$ (2)

实际上，滑动模态将存在于滑模切换面 $s=\text{0}$ 的一个 $\Delta$ 邻域内，即带宽 $S_{\text{Δ}}=\left\{x\Vert s\left(\text{x}\right)\Vert \le \text{Δ}\right\}$ 。因此，将等效控制中得到的理想滑动模态近似等于实际滑动模态进行研究尤为必要，而滑模近似原理对于时滞广义系统的研究提供了理论支撑，高存臣 [48] 等已详细给出了系统(2)的滑模近似原理的证明及其应用。

3.2. 受限综合法

受限综合法 [48] ，即对具有固定结构的非线性时滞时变广义系统，先进行受限等价变换，然后再研究该系统的综合问题，考虑如下系统：

$\{\begin{array}{l}E\stackrel{\dot{}}{x}\left(t\right)=A\left(t\right)x\left(t\right)+f\left(t,x\left(t\right),x\left(t-\tau \right)\right)+B\left(t\right)u\left(t\right)\\ x\left(t\right)=\phi \left(t\right),t\in \left[-\tau ,0\right]\end{array}$ (3)

对于系统(3)，任给 $t\in \left[0,+\infty \right]$ ， $rank\left(E,B\left(t\right)\right)=n$ ，矩阵函数 $B\left(t\right)$ 列满秩，则存在可逆矩阵函数 $P\left(t\right),Q\left(t\right)$ 使得以下两项成立：

1) 若 $rank\left(B\left(t\right),f\right)=rank\left(B\left(t\right)\right)$ ，则系统(3)受限等价于：

$\{\begin{array}{l}\stackrel{\dot{}}{x}\left(t\right)=A_{\text{11}}\left(t\right)x_{\text{1}}\left(t\right)+A_{\text{12}}\left(t\right)x_{\text{2}}\left(t\right)\\ \text{0}=A_{\text{21}}\left(t\right)x_{\text{1}}\left(t\right)+A_{\text{12}}\left(t\right)x_{\text{2}}\left(t\right)\\ +f_{\text{2}}\left(t,x_{\text{1}}\left(t\right),x_{\text{2}}\left(t\right),x_{\text{1}}\left(t-\tau \right),x_{\text{2}}\left(t-\tau \right)\right)+B_{\text{2}}\left(t\right)u\left(t\right)\\ \left[\begin{array}{c}{x}_{\text{1}}\left(t\right)\\ x_{\text{2}}\left(t\right)\end{array}\right]=P^{-\text{1}}\phi \left(t\right)=\left[\begin{array}{c}{\phi }_{\text{1}}\left(t\right)\\ {\phi }_2\left(t\right)\end{array}\right],t\in \left[-\tau ,0\right]\end{array}$ (4)

2) 若 $rank\left(B\left(t\right),f\right)\ne rank\left(B\left(t\right)\right)$ ，则系统(3)受限等价于：

$$ (5)

对于受限综合法，先进行受限等价分解变换，经过非奇异的变换无论是连续系统还是离散系统不改变其广义系统的结构性质；通过等价分解，将高维系统转化为低维子系统，然后分别再利用综合法设计滑模面和控制器。无论是在计算上还是在控制律的设计上，都给研究广义系统带来便利。因此利用受限综合法研究广义系统尤为必要。

3.3. 软变结构控制法

软变结构控制 [49] [50] ，是一种无滑模变结构控制，通过连续的选择参量来改变控制器结构以实现状态信号变化。软变结构控制策略具有调节精度高，响应速度快，并可以有效的削弱系统抖振等优点，从而使得该系统在整个状态空间具有良好的动态性能。Liu [50] 等通过设计了一种动态软变结构控制器，可有效抑制系统的抖振，研究了一类广义系统的动态软变结构问题，从而提高了该系统的动态品质；Liu [51] 等针对一类L-可控广义系统，提出了一种新的软变结构控制方案；Röthig [52] 等基于软变结构控制法，设计了一种非饱和控制律，研究了一类线性系统的镇定性问题。软变结构控制策略的控制算法设计主要有3种 [50] ：1) 基于Lyapunov隐函数软变结构控制；2) 动态软变结构控制；3) S-型函数软变结构控制。

考虑如下系统：

$\stackrel{\dot{}}{x}\left(t\right)=Ax\left(t\right)+bu\left(t\right)$ (6)

其中， $x\left(t\right)\in R^n$ 为系统的状态向量， $u\left(t\right)\in R$ 为控制输入向量， $A\in R^{n\times n}$ 为常数矩阵， $b\in R^n$ 为常数向量，且 $\left(A,b\right)$ 是能控的。而在实际的生活中，一般情况下控制输入是受限制的，为此进行假设：

$\left|u\left(t\right)\right|\le u_0$ (7)

其中 $u_0$ 是正常数。

基于Lyapunov隐函数软变结构控制：在有限个子控制器的无滑模变结构控制器中，一般设计子控制器为线性反馈控制器：

$u\left(t\right)=-k_p^{T}x\left(t\right),p=1,2,\cdots ,k$ (8)

其中 $k_{\text{p}}\in R^n$ 为常值向量。

2) 动态软变结构控制：假设所选择的策略参量 $p$ 满足 $\stackrel{\dot{}}{p}=f\left(p,x\right)$ ，则设计的控制器为：

$u=-g^{T}x-p{h}^{T}x$ (9)

其中 $g,h\in R^n$ 都是 $n$ 维列向量。记 $A_{\text{0}}=A-b{g}^{\text{T}}$ ，则可得到闭环控制系统：

$\stackrel{\dot{}}{x}=\left(A-b{g}^T\right)x-pb{h}^{T}x=\left(A_0-pb{h}^T\right)x$ (10)

3) S-型函数软变结构控制：构造两个向量 $k_{\text{1}}\in R^n,k_{\text{2}}\in R^n$ ，使得

(11)

其中， $u_{\text{1}}$ 是线性控制器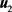，为基于双曲正切函数的软变结构控制器，构造控制器如下：

$u=u_{\text{1}}+u_{\text{2}}$ (12)

得到闭环软结构控制系统：

$\stackrel{\dot{}}{x}=\left(A-b{k}_1{}^T-\rho \phi b{k}_2{}^T\right)x\underset{\_}{\underset{\_}{\Delta }}\bar{A}\left(\rho \right)x$ (13)

3.4. 趋近律法

3.4.1. 趋近律的研究状况

趋近律方法是研究滑模控制的常用方法，自1995年高为炳院士提出离散滑模控制系统的指数趋近律开始，国内外学者们便基于趋近律方法来研究滑模控制，设计的控制律简单并且容易实现，但是存在的一个缺点是系统会产生抖振。那么如何削弱抖振呢，又成为学者们研究的一个新领域。近两年来，Latosiński [53] 等设计了一种新的基于趋近律的离散系统滑模控制器，这种趋近律与大多数现有方法相反，新策略设计使用具有相对度2的滑动变量，即：

$\begin{array}{c}{s}_2\left(k+2\right)=f\left[s_2\left(k+1\right)\right]f\left[s_2\left(k\right)\right]s_2\left(k\right)-\alpha \mathrm{sgn}\left[s_2\left(k+1\right)\right]-f\left[s_2\left(k+1\right)\right]\alpha \mathrm{sgn}\left[s_2\left(k\right)\right]\\ +c_2{}^{\text{T}}Ab\bar{\alpha }\left(k\right)+c_2{}^{\text{T}}Abd\left(k\right)-d_2\end{array}$ (14)

该趋近律既保证了系统期望的动态特性，又将滑模变量驱动到比其相对度1更窄的准滑动模带；针对多输入多输出非线性系统，Devika [54] 等提出了两种改进的滑动趋近律方法，既保证了系统状态可以快速到达滑动面，又具有可以削弱系统抖振；Liu [55] 等又提出了一种新型指数趋近律：

$\stackrel{\dot{}}{S}=-\frac{k{\left|s\right|}^{\alpha }}{N\left|s\right|}sign\left(S\right)$ (15)

其中 $N\left(S\right)=\beta +\left(1-\beta \right){\text{e}}^{-\gamma {\left|s\right|}^{\mu }}$ ， $\alpha ,\beta ,\gamma ,\mu$ 都是正数，且 $0<\alpha ,\beta <1$ 。此控制律能够有效抑制系统抖振，加快系统的逼近过程。Wang [56] 等提出了一种新的针对分数阶非奇异终端滑模控制趋近律，即采用快速TSM型趋近律，使得系统状态可以在有限时间内到达滑动模态，并做滑动运动。

3.4.2. 理想趋近律与扰动补偿趋近律

趋近律是一种理想的不产生抖振的滑动模态轨迹，而在实际生活中，由于建模以及不确定因素的估计，在设计滑模面的过程中总会产生抖振，对此期望有一种滑模，不仅是无抖振的而且要在有限时间到达滑模面。

理想趋近律：为了研究非匹配离散广义系统的滑模控制策略，宋 [57] 等给出了理想趋近律的概念。理想趋近律是一种可以人为预先设定的满足无抖振(实际为微抖振)特征，并在有限时间内可到达滑模面，并稳定于切换面的理想滑动模态轨迹，它需具备三个条件：1) 简单易实现；2) 有限时间内快速到达滑模面；

3) 稳定于切换面时速度趋于零，即 $\underset{k\to \infty }{\lim }s\left(k+1\right)=s\left(k\right)$ 。

扰动补偿趋近律：为了有效的削弱系统的抖振，瞿 [58] 等给出了一种带有扰动补偿的趋近律：

$s\left(k+1\right)=\left(1-qT\right)s\left(k\right)-\epsilon Tsgns\left(k\right)+c^{\text{T}}g\left(k\right)-\rho sgns\left(k\right)-{\displaystyle \underset{i=2}{\overset{k}{\sum }}\left[s\left(i\right)-I\left(\alpha \right)s\left(i-1\right)+\rho sgns\left(i-1\right)\right]}$ (16)

3.5. 受限等价法

受限等价变换：如果对于两个广义系统，经过非奇异线性变换后，前后状态是保持一致(一一对应的)，则称这两个广义系统是受限等价的，而所进行的非奇异线性变化为受限等价变换。受限等价变换不改变广义系统的结构性质(如正则性、稳定性、可控性、可观性、传递函数、特征值等)。在时滞连续广义系统不确定的滑模控制策略和时滞连续广义系统不确定的滑模控制策略中，受限系统等价分解法极为重要。线性广义系统经过受限等价分解可以化为标准型，在标准型下系统的某些结构性质更加直观明了便于研究。刘 [59] 给出了以下三种标准型式：1) Kronecker标准型；2) 微分反馈标准型；3) 动态分解标准型。

受限等价法在时滞广义系统中的应用十分广泛，高 [48] 等对于以下四种情况进行了考虑，分别进行受限等价分解，再设计不同的滑模控制律，来研究多个系统的稳定性问题。

1) 非结构式扰动的单时滞情况；2) 具有结构式扰动的单时滞情况；3) 非结构式扰动的多时滞情况；4) 具有结构式扰动的多时滞情况。

受限综合法与受限等价法之间的区别：受限综合法是指研究系统的性质(如稳定性、鲁棒性)时有些变量受到一定限制；受限等价法是指研究系统的等价性(如稳定性等价性)时有些变量有一定限制。

3.6. 自适应滑模控制法

自适应控制主要是针对系统的不确定性因素进行控制，即所设计的控制器能够根据外界的干扰以及自身的不确定因素来进行自行调整已求达到最优的控制性能。外界的干扰不可避免，系统在建模的过程中的不确定性影响因素也不可避免。随着科学技术进步和控制系统复杂性的增加，自适应滑模控制法尤为重要，将自适应滑模控制法与其他理论方法相结合，能够更有效的研究不同系统的动态性能。近年来，国内外学者对于自适应滑模控制理论的研究不断深入。Benamor [60] 等研究了一类不确定离散时变时滞系统的鲁棒自适应控制问题，通过定义一类新的鲁棒自适应滑模控制方法估计了不确定性的上限。控制律如下：

$u\left(k\right)=-{\left(CB\right)}^{-1}\left[CBKx\left(k\right)+Ksign\left(s\left(k\right)\right)+sign\left(s\left(k\right)\right)A_x\right]$ (17)

其中：

$sign\left(s\left(k\right)\right)=\left[\begin{array}{c}sign\left(s_1\left(k\right)\right)\\ ⋮\\ sign\left(s_m\left(k\right)\right)\end{array}\right]$ ， $K=\left[\begin{array}{ccc}{K}_1& 0& 0\\ 0& \ddots & 0\\ 0& 0& K_m\end{array}\right]$

Gracia [61] 等研究了一类机器人自适应滑模控制问题，通过考虑和比较几种自适应开关增益，来分析所产生的不稳定性及其其他性能；Liu [62] 等研究的是一类离散非线性系统的无记忆自适应滑模控制，设计的控制器如下所示：

$u_k=u_{k-1}+{\Phi }_{2,k}^{-1}\left(e_k-\Delta y_k{\Phi }_{1,k}-\frac{{\bar{\epsilon }}_{k+1}\left(\eta {\theta }_k+1-\eta \right)-{\underset{\_}{\epsilon }}_{k+1}}{\eta {\theta }_k+2-\eta }{\vartheta }_{k+1}\right)+{\Phi }_{2,k}^{-1}{\Lambda }_s\text{sign}\left(s_k\right)$ (18)

主要针对具有跟踪误差约束的离散时间非线性过程，提出了一种新的基于数据驱动的无记忆自适应滑模控制策略；Mofid [63] 等基于自适应控制方法，研究了一类具有参数不确定的四转子无人机稳定性问题；Riani [64] 等针对一类非线性系统的未知但有界的不确定性问题，提出了一种积分型的鲁棒自适应滑模控制策略，控制器如下：

$u={\phi }^{-1}\left[{\ddot{q}}_d+\alpha {\stackrel{\dot{}}{e}}^{\frac{q}{p}}+\beta e^{\frac{q}{2p-q}}-f+\lambda s+{\phi }^T\hat{A}\frac{s}{\Vert s\Vert }\right]$ (19)

Zhang [65] 等是采用鲁棒自适应积分滑模控制方法，提出了一种基于动态滞后补偿的控制方法，研究了一类具有时间滞后和不确定性的系统的稳定性问题，设计了一种自适应律来估计积分滑模控制器的增益，从而削弱了系统抖振，且不再需要先验的不确定性上界有界的约束条件。采用自适应滑模控制法来设计控制器，不仅能够保证系统的鲁棒性，而且能够对系统的不确定性和外界干扰性进行补偿。

3.7. 随机广义控制法

广义系统具有层次性结构，并且广义系统的模型是建立在奇异摄动概念的基础上，它的解结构比较复杂。随机现象包含了很多不确定因素，因此研究随机广义系统的动态性能特别必要，近年来，国内外许多学者也开始对随机广义系统进行了深入研究。其中，Gao [66] 等研究了一类具有时滞脉冲和马尔可夫切换的广义随机脉冲微分方程的指数稳定性，针对大时滞、小时滞的脉冲控制问题，提出了一种新的脉冲和开关时序的子序列方法；Blom [67] 等研究了一类广义随机混合系统的到达概率估计问题；Zhang [68] 等研究了一类具有随机模式切换的混合线性变参数系统的稳定性和镇定性问题；Wang [69] 等研究了一类具有广义Prandtl-Ishlinskii滞后的反馈随机非线性系统的鲁棒自适应神经网络控制问题；Zhuang [70] 等研究了一类具有时滞的随机广义马尔可夫跳跃系统的可容许性分析和镇定问题，并设计了状态反馈控制器，保证了系统的稳定。

时滞现象在物质世界中普遍存在的，随机更是世界的本性特征。为此，对于随机广义系统的研究更为必要，其研究成果奖不断丰富控制理论体系。

4. 几个新的研究方向

结合本文所论述的时滞广义变结构控制方法，现提出几个在国际学术界最热门的研究方向：

1) 模糊时滞广义VSC系统的分析与综合；2) 冗余时滞广义VSC系统的分析与综合；3) 不确定时滞广义VSC系统的分析与综合；4) 随机时滞广义VSC系统的分析与综合；5) 分布参数时滞广义VSC系统的分析与综合；6) 时滞广义VSC系统的定向分析综合与应用；7) 时滞广义VSC系统的智能控制理论与应用；8) 时滞广义VSC系统在各类实际中的应用分析；9) 基于神经网络的时滞广义VSC系统的应用研究；10) 分数阶时滞广义VSC系统的分析与综合；11) 耦合时滞广义VSC系统的分析与综合；12) 混沌时滞广义VSC系统的分析与综合等。

5. 结语

本文首先介绍了时滞广义变结构控制理论的研究进展，同时对于变结构控制以及广义系统进行概述；其次，介绍了研究上述系统常用的七种控制方法，包括滑模近似法、受限综合法、软变结构控制法、趋近律法、受限等价法、自适应滑模控制法及随机广义控制法，并对每一种方法的研究状况进行概述；最后，提出了几个热门的研究课题。

基金项目

在此对“山东省自然科学基金资助项目(编号ZR2017QF011)，山东省高等学校科技计划项目(编号J16LB10)和潍坊市科技发展计划项目(编号2017GX017)”的资助表示感谢。

文章引用

张 利,高存臣,刘云龙. 时滞广义变结构控制研究新进展
New Research Advance of Variable Structure Control Singular Systems with Time Delays[J]. 动力系统与控制, 2018, 07(04): 337-347. https://doi.org/10.12677/DSC.2018.74038

参考文献