Dynamical Systems and Control
Vol.
08
No.
02
(
2019
), Article ID:
29574
,
11
pages
10.12677/DSC.2019.82015
Analysis, Control and Circuit Implementation of a Novel 4D Chaotic System
Zhili Wang1,2, Hong Niu1, Dechu Tan1,3
1College of Electronic Information and Automation, Tianjin University of Science & Technology (TUST), Tianjin
2School of Electrical and Information Engineering, Tianjin University (TJU), Tianjin
3School of Automation and Electrical Engineering, University of Science and Technology Beijing (USTB), Beijing
Received: Mar. 11th, 2019; accepted: Mar. 22nd, 2019; published: Apr. 3rd, 2019

ABSTRACT
The dynamics of the novel four-dimensional (4D) chaotic system are presented. The analog circuit is derived from the modified module-based approach to chaotic circuit design and implemented by means of the A + D Lab platform to illustrate that the novel 4D chaotic system could generate chaos on hardware. For chaos control of the novel 4D chaotic system, the mathematical model of the controlled system is formulated, and a linear feedback controller only with one variable is designed based on the Lyapunov stability theory and implemented by circuit. The output signals of the circuit implementation show that the state variables of the controlled novel 4D chaotic system are no longer chaotic or periodic but asymptotically converge to zero, which indicates that the controlled system is asymptotically stable at the origin and the linear feedback controller is feasible and effective.
Keywords:Chaos, Novel Four-Dimensional Chaotic System, Chaos Control, Circuit Implementation
一个新四维混沌系统的分析、控制与电路实现
王志礼1,2,牛弘1,谭得楚1,3
1天津科技大学,电子信息与自动化学院,天津
2天津大学,电气自动化与信息工程学院,天津
3北京科技大学,自动化学院,北京
收稿日期:2019年3月11日;录用日期:2019年3月22日;发布日期:2019年4月3日

摘 要
本文首先对新四维混沌系统的动力学特性进行分析。而后,采用改进型模块化混沌电路设计方法设计新四维混沌系统的电路模型并于A + D Lab实验平台上搭建其模拟电路实现,从硬件上验证该新四维混沌系统可产生混沌运动现象。针对新四维混沌系统的稳定性控制,本文通过建立被控新四维混沌系统的数学模型,基于Lyapunov稳定性理论,设计单变量线性反馈控制器并搭建其硬件电路实现,从硬件上验证被控新四维混沌系统不再产生混沌或周期运动而是渐近稳定于平衡点原点,以及所设计的线性反馈控制器的可行性与有效性。
关键词 :混沌,新四维混沌系统,混沌控制,电路实现

Copyright © 2019 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
高维混沌系统维数高、动力学特性更为复杂,一直是混沌研究领域的研究热点内容之一 [1] [2] [3] [4] 。本文作者于文献 [5] 中提出一个新四维混沌系统,并于文献 [6] 中采用改进型模块化混沌电路设计方法设计了该新四维混沌系统的电路模型。同时,本文作者于文献 [5] 中基于Lyapunov稳定性理论设计出单变量线性反馈控制器,使新四维混沌系统不再产生混沌或周期运动,而是渐近稳定于平衡点原点。进一步,本文作者于文献 [5] [6] 中借助Matlab数值仿真软件和Multisim电路仿真软件,绘制了新四维混沌系统的相轨迹曲线,验证了所设计的电路模型的正确性以及线性反馈控制器的可行性与有效性。然而,针对该新四维混沌系统及其稳定性控制的硬件电路实现尚未给出。
本文基于文献 [5] [6] ,对新四维混沌系统的动力学特性进行扩充,给出对于系统对称性、耗散性、平衡点特性、初值敏感性以及混沌吸引子的具体分析。在此基础上,采用“A + D Lab 理工实验室”模拟数字混合贯穿式智慧实验平台搭建新四维混沌系统及其被控系统的硬件电路实现,从硬件上验证新四维混沌系统中混沌现象的存在性以及所设计的单变量线性反馈控制器的控制效果。
2. 新四维混沌系统的动力学特性分析
2.1. 数学模型
新四维混沌系统的数学模型如下所示
(1)
其中, 为系统的状态变量, , , , , 为新四维混沌系统(1)的典型参数。
2.2. 对称性
新四维混沌系统(1)关于 轴对称,即通过坐标变换 ,系统的数学模型不发生改变。
2.3. 耗散性
新四维混沌系统(1)满足如下等式
则新四维混沌系统(1)始终是耗散的,系统状态的变化是有界的。
新四维混沌系统相体积的指数衰减率可表示为
即一个初始体积为 的体积元经过时间 收缩为体积元 [7] 。这意味着,当 时,包含系统轨线的每个体积元以指数速率 收缩到0。因此,当 时,系统吸引子的整数维体积为零。
2.4. 平衡点分析
令式(1)的右边为0,可得新四维混沌系统(1)的平衡状态方程为
(2)
解方程组(2),令
可得新四维混沌系统(1)共有3个平衡点,分别为
现以平衡点 为例对平衡点处的相关特性进行分析。通过在平衡点 处对系统(1)进行线性化,得其Jacobian矩阵为
其特征方程为
将 , , , , 代入上式,求得其特征根分别为
其中, , ,则平衡点 为一不稳定平衡点。其余2个平衡点的分析方法与此处相同,各平衡点的性质分别如表1中所示。
Table 1. Properties of equilibrium points of the novel 4D chaotic system
表1. 新四维混沌系统各平衡点的性质
2.5. 初值敏感性
将新四维混沌系统(1)的状态变量的初始值分别设定为 和 ,并保持其他条件均不变,利用Matlab数值仿真软件,绘制出新四维混沌系统(1)在不同初始值下的解曲线,如图1中所示。

Figure 1. Curves of state variables of the novel 4D chaotic system (1) under different initial values: (a) t-x; (b) t-y; (c) t-z; (d) t-w
图1. 新四维混沌系统(1)在不同初始值下的解曲线:(a) t-x; (b) t-y; (c) t-z; (d) t-w
从图1中可以明显地看出,其他条件均保持不变,仅仅是将新四维混沌系统(1)中 的初始值变化了 ,经过很短的一段时间后,系统解曲线的变化明显,说明新四维混沌系统(1)具有初值敏感性,初值敏感性是混沌运动的一个重要特征。
2.6. 新四维混沌系统的混沌吸引子
令新四维混沌系统(1)的初值为 ,通过数值仿真可求得系统的Lyapunov指数分别为 , , , ,说明此时新四维混沌系统产生混沌运动。由此可计算出新四维混沌系统(1)的Lyapunov维数 为
(3)
其中, 是使 的最大整数 [8] 。由式(3)可知, 为一分数维。新四维混沌系统(1)的各相轨迹曲线如图2中所示。

Figure 2. Phase portraits of the novel 4D chaotic system (1): (a) x-y; (b) x-z; (c) x-w; (d) y-z; (e) y-w; (f) z-w
图2. 新四维混沌系统(1)的相轨迹曲线:(a) x-y; (b) x-z; (c) x-w; (d) y-z; (e) y-w; (f) z-w
由上述分析可知,由于新四维混沌系统(1)具有耗散性,因此,做混沌运动的新四维混沌系统(1)从整体来说是稳定的,吸引子外的一切轨线最后都要收缩进入到吸引子中。但就局部而言,吸引子内的运动又是不稳定的,相邻轨道要相互排斥而按指数形式分离,从而不具有轨道稳定性且具有初值敏感性。所以,新四维混沌系统(1)的混沌吸引子是整体稳定性和局部不稳定性的矛盾结合体,具有复杂结构 [8] 。
3. 新四维混沌系统的电路设计与硬件实现
3.1. 电路设计
本文作者于文献 [6] 中应用改进型模块化混沌电路设计方法设计出新四维混沌系统(1)的模拟电路模型,主要过程包括变量比例压缩变换、时间尺度变换、标准形式变换、电路模型设计、元件参数确定五个步骤 [9] ,即令 , , , ,并代入式(1)。为简化标记,仍将 , , , 记为 , , , 。同时,为便于电路实现,对系统进行时间尺度变换并改写为标准形式,则
(4)
其中, 。
由式(4)设计相应的改进型模块电路并将输入、输出项对应连接,可得系统(4)的电路模型,如图3中所示。

Figure 3. Circuit model of the system (4)
图3. 系统(4)的电路模型
由图3,可得该电路模型的状态方程为
(5)
令式(5)与式(4)中对应项系数相等,已知 , ,则 , , , , , , 。
3.2. 硬件实现
本文应用“A + D Lab 理工实验室”模拟数字混合贯穿式智慧实验平台搭建并观测如式(5)所示的新四维混沌系统的模拟电路硬件实现。本文中所采用的运算放大器的型号均为TL082CP,乘法器的型号均为AD734AN,电源供电电压均为 。新四维混沌系统的模拟电路硬件实现如图4中所示。硬件电路运行产生的实际相轨迹曲线如图5中(a)~(f)中所示。
逐一对比图5中(a)~(f)与图2中(a)~(f),考虑到硬件电路中各元器件的精度均有限,且不可避免地存在导线电阻等外加参数摄动,使得实际电路中各参数与图3中对应参数间存在偏差。但从定性分析的角度出发,仍可认为图5中的实际电路输出曲线与图2中的软件数值仿真曲线相一致,并基于此认为实际电路的参数是正确的,可用于本文中对于新四维混沌系统硬件部分的后续研究。

Figure 4. Circuit implementation of the novel 4D chaotic system
图4. 新四维混沌系统的模拟电路硬件实现
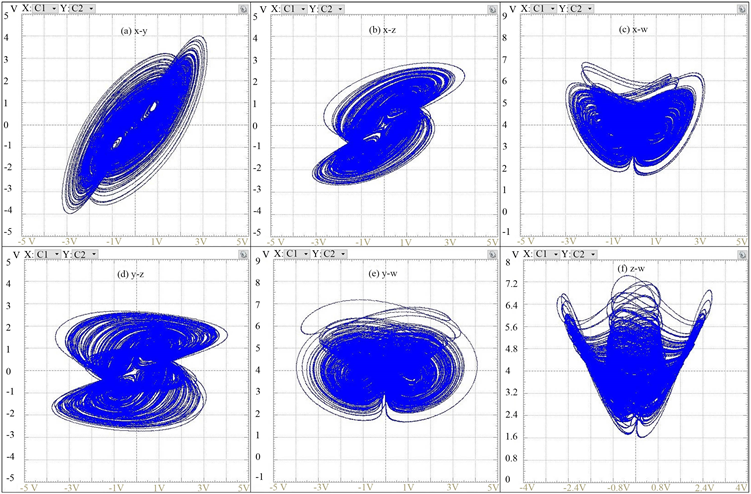
Figure 5. Phase portraits of the circuit implementation: (a) x-y; (b) x-z; (c) x-w; (d) y-z; (e) y-w; (f) z-w
图5. 硬件电路运行产生的实际相轨迹曲线:(a) x-y; (b) x-z; (c) x-w; (d) y-z; (e) y-w; (f) z-w
4. 新四维混沌系统的稳定性控制
4.1. 控制器设计
本文作者于文献 [5] 中详细介绍了新四维混沌系统(1)的稳定性控制过程,即通过设计线性控制器,使新四维混沌系统(1)不再产生混沌或周期运动,而是渐近稳定于平衡点原点,并通过数值仿真验证了所设计的控制器的可行性与有效性。主要结论如下:令 ,其中 为系统(1)的状态变量, 为原点,则被控系统可表示为
(6)
其中,
(7)
为待设计的线性反馈控制器。由文献 [5] 可知,可取径向无界的正定函数
作为被控系统(6)的Lyapunov函数,其导数为

Figure 6. Curves of state variables of circuit implementation of the controlled novel 4D chaotic system: (a) t-x; (b) t-y; (c) t-z; (d) t-w
图6. 被控新四维混沌系统硬件电路实现中各状态的控制效果:(a) t-x; (b) t-y; (c) t-z; (d) t-w
文献 [5] 中已经证明,可取 ,则当
是负定的。又由于 是径向无界的,所以被控系统(6)在原点处是全局渐近稳定的。现取 ,则控制器 可表示为
(8)
将式(8)代入式(6),仍将被控系统(6)的初始值设为 ,得被控系统(6)的Lyapunov指数分别为 , , , ,均为负值,说明被控系统(6)渐近稳定于平衡点原点,不再产生混沌或周期运动。
4.2. 被控系统的电路实现
仍采用改进型模块化电路设计的方法设计控制器 的模拟电路实现。对式(8)进行变量比例压缩变换和时间尺度变换并改写为标准形式,则
(9)
由式(9)可设计出控制器 的改进型模块电路,如图3中红色方框中所示。
控制器 的硬件电路实现如图4中红色方框中所示。闭合开关S1,硬件电路中各状态的控制效果如图6中所示。可以看出,加入控制器后,各状态曲线不再产生混沌或周期运动而是渐近稳定于零平衡状态,说明所设计的控制器可有效控制系统使其不再产生混沌或周期运动,而是渐近稳定于平衡点原点。
5. 结论
本文通过分析新四维混沌系统的对称性、耗散性、平衡点特性、初值敏感性和混沌吸引子特性,从理论上说明了新四维混沌系统中混沌现象的存在性。在此基础上,本文采用“A + D Lab 理工实验室”模拟数字混合贯穿式智慧实验平台搭建了新四维混沌系统及其被控系统的硬件电路实现,使用板载 直流电源,借助WaveForms应用软件,将笔记本电脑显示屏作为示波器显示新四维混沌硬件系统的输出信号,有效简化了实验设备,方便对输出信号的观测、读取和存储;与此同时,从硬件上观测到了新四维混沌系统产生的混沌吸引子,并验证了所设计的单变量线性反馈控制器对于控制被控新四维混沌系统使其不再产生混沌或周期运动的可行性与有效性。本文所设计的新四维混沌系统的硬件电路实现还可用于诸如混沌同步、保密通信等的研究中。
致谢
感谢“天津科技大学青年教师创新基金”、“天津市普通高等学校本科教学质量与教学改革研究计划项目(一般项目:171005704B)”、“‘十三五综投’天津市应用型专业建设项目”、“天津科技大学教改项目(一般项目:10375)”对本文的资助。
文章引用
王志礼,牛 弘,谭得楚. 一个新四维混沌系统的分析、控制与电路实现
Analysis, Control and Circuit Implementation of a Novel 4D Chaotic System[J]. 动力系统与控制, 2019, 08(02): 129-139. https://doi.org/10.12677/DSC.2019.82015
参考文献
- 1. 付宏睿, 董永刚, 张建刚. 基于新四维混沌系统的复杂网络的混沌保密通信及噪声研究[J]. 东北师大学报(自然科学版), 2018, 50(4): 73-77.
- 2. 王磊, 张勇, 舒永录. 一类高维混沌模型的动力学分析及数值仿真[J]. 数学的实践与认识, 2018, 48(12): 220-226.
- 3. 朱建良, 赵洪超. 一个新的四维混沌系统及其电路实现[J]. 哈尔滨理工大学学报, 2010, 15(2): 4-8.
- 4. 张宇辉, 齐国元, 刘文良, 阎彦. 一个新的四维混沌系统理论分析与电路实现[J]. 物理学报, 2006, 55(7): 3307-3314.
- 5. Niu, H. (2017) Analysis and Control of a Novel 4D Chaotic System. The 2017 International Conference on Artificial Life and Robotics, Miyazaki, 19-22 January 2017, 165-168.
- 6. Tan, D.C. and Niu, H. (2018) Analog Circuit Design of a Novel 4D Chaotic System. The 2018 International Conference on Artificial Life and Robotics, Oita, 1-4 February 2018, 574-577.
https://doi.org/10.5954/ICAROB.2018.OS15-1 - 7. 陈关荣, 吕金虎. Lorenz系统族的动力学分析、控制与同步[M]. 北京: 科学出版社, 2003: 9-10.
- 8. 张国山, 牛弘. 一个基于Chen系统的新混沌系统的分析与同步[J]. 物理学报, 2012, 61(11): 110503-1-11.
- 9. 禹思敏. 混沌系统与混沌电路——原理、设计及其在通信中的应用[M]. 西安: 西安电子科技大学出版社, 2011: 300-312.
