 Modern Physics 现代物理, 2013, 3, 65-67 http://dx.doi.org/10.12677/mp.2013.32012 Published Online May 2013 (http://www.hanspub.org/journal/mp.html) Excitation Energies and Fine Structure Splittings for 1s2nd (n 9) States of Ni25+ Ion* Ning Xu1, Xuefei Han2, Yingying Gu2, Shuai Wang2, Muhong Hu2 1The Fourth Senior High School of Changtu, Tieling 2School of Physics and Electronic Technology, Liaoning Normal University, Dalian Email: humuhong@163.com Received: Apr. 13th, 2013; revised: May 1st, 2013; accepted: May 9th, 2013 Copyright © 2013 Ning Xu et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unre- stricted use, distribution, and reproduction in any medium, provided the original work is properly cited. Abstract: The excitation energies and fine structure splittings of 1s2nd (n 9) states for Ni25+ ion are calculated in this paper. Non-relativistic energies are obtained with the eigenvalue of non-relativistic Hamiltonian operators; the relativis- tic and mass-polarization effects on the energies are included as the first-order perturbation. The fine structure splittings are determined from the expectation value of spin-orbit and spin-other orbit interaction operators. In order to make the results more precise, quantum-electrodynamics (QED) contribution and higher-order relativistic contribution are con- sidered for highly charged Ni25+ ion. The results of fine structure splittings agree with the experimental data excellently, and the error is no more than several cm−1. Compared the excitation energy calculated with experimental data, the rela- tive error is only 0.2‰ - 0.6‰. It indicates the results obtained in this paper are both reliable and accurate. Keywords: Ni25+ Ion; Excitation Energy; Fine Structure Splittings Ni25+离子 1s2nd (n 9)的激发能和精细结构* 徐 宁1,韩雪飞 2,顾莹莹 2,王 帅2,胡木宏2 1辽宁省昌图县第四高级中学,铁岭 2辽宁师范大学物理与电子技术学院,大连 Email: humuhong@163.com 收稿日期:2013 年4月13 日;修回日期:2013年5月1日;录用日期:2013 年5月9日 摘 要:本文主要计算1s2nd (n 9)态的激发能和精细结构劈裂。非相对论能量通过求解 Hamiltonian 算符本征 值的极值获得,然后将相对论 效应和 质量极 化效应 的贡献 作为一 级微扰 来处理 。精细 结构劈 裂数值 由自旋 –轨 道相互作用算符和自旋–其他 轨道相 互作用 算符的 期待值 得到。 为了获 得高精 度的计 算结果 ,在类 氢近似 下估 算高阶相对论修正和量子电动力学(QED)修正对能级结构 的贡献。本文 得到的精细结 构的计算结果 与实验相 差 只有几个cm−1,激发能的计算结果与实验相比,相对误差只有0.2‰~0.6‰,由此表明本文获得的理论数据精度 较高,采用的理论方法是合理可靠的。 关键词:Ni25+离子;激发能;精细结构 1. 引言 近年来,在诸多高新技术领域需求和相关实验技 术发展的推动下,尤其是以光电离和电子碰撞电离为 主要机制的产生高荷电离子(HCI)实验装置的问世,使 得对高离化原子的结构和性质的研究成为当代国际 原子物理中一个十分活跃领域。但是,目前关于这方 资助信息:国家自然科学基金(编号:11074102),国家自然科学基 金(编号:11204118)。 Copyright © 2013 Hanspub 65  Ni25+离子 1s2nd (n 9)的激发能和精细结构 面的实验数据还很少,而且现有的数据的精度也不是 很高,在很多情况下还有赖于准确的理论预言[1,2],因 此对高荷电离子能级结构高精度的理论计算具有重 要的研究意义。 本文计算Ni25+离子 1s2nd态的非相对论能量,将 相对论和质量极化效应作为微扰,以此为基础,通过 引入价电子感受的有效核电荷概念,在类氢近似下估 算相对论效应对体系能量的高阶相对论修正和 QED 修正,完成该离子1s2nd的激发能、精细结构的理论 计算。 2. 理论方法 本文采用理论方法的详细描述可参见文献[3],这 里不再赘述。对于1s2nd组态的三电子体系,采用变分 波函数[3]: 13 , 1, 2,31, 2333 1, 2, 3 ir si li ini li AdreY i C i (1) 其中 A是反对称化算符,式中的线性参数通过求解体 系的久期方程确定,非线性参数则在寻求体系能量极 值的过程中加以优化。在此过程中得到体系非相对论 能量 E0,同时体系的波函数得以确定。随着核电荷数 的增加,相对论效应更加显著,因此必须考虑相对论 效应对体系能级结构的影响。本文中,相对论效应和 质量极化效应用一级微扰论计算: 12 345 12 EHH HHH EE (2) 其中 E1是来自单粒子微扰算符(电子动能修正和 Darwin 项)的一阶能量修正, E2是来自双粒子算符(电 子接触项、轨道–轨道相互作用以及质量极化效应) 的贡献,这些算符的具体表达式可参见文献[3],而高 阶相对论效应和量子电动力学效应(QED)的详细考 虑过程见文献[4]。至此,体系能量计算完毕,表示 为: totalnonrel1 .higher.QED g ord relord rel EE EEE (3) 非相对论效应中的自旋效应可导致能级的精细 结构劈裂,其中包括电子的自旋算符与其自身的轨道 算符相互作用、电子的自旋算符与其他电子的轨道算 符相互作用。具体的精细结构劈裂数值可由自旋–轨 道相互作用算符(HSO)和自旋–其他轨道相互作用算 符(HSOO),计算其在 LSJ 耦合表象下的期待值而得到, 所以非相对论修正引起的精细结构劈裂 S f s E为: S f sJ SOSOOJ ELSJMHHLSJM (4) 为了使结果更为准确,还要计及高阶相对论效应 和QED 效应,精细结构总劈裂值为: QED QED HJ fs fsfs EEEE (5) 3. 结果与讨论 Ni25+离子 1s2nd (n ≤ 9)的精细结构的计算结果列 于表 1中。从该表中可以看到,本文考虑各种物理效 应后得到的计算结果与已有实验数据的偏差仅有几 个cm−1,二者非常接近,远远小于实验误差。由此可 见,本文得到的理论结果具有一定的精度,是准确可 靠的。从该表还可以看出,随着主量子数的增加,1s2nd 态Rydberg 序列的精细结构劈裂值不断减小,这与导 致精细结构的主要机制自旋–轨道相互作用随着主 量子数的增大而减弱的变化规律完全一致。 表2中给出 Ni25+离子1s2nd态的激发能的计算结 果,在考虑相对论修正和QED 修正后得到的结果与 现有实验数据符合的很好,相对误差大约在0.2‰~ 0.6‰。目前,跃迁能的理论计算和实验数据还存在一 些空白,希望本文的计算结果能够对后续的理论研究 和实验工作提供一些有益的参考。 图1直观的给出了 1s23d~1s2nf (4 ≤ n ≤ 9)态之间 的跃迁的格罗出图。1s2nf之间的能级间隔和波长,从 图中可以看到对于 1s2nf (4 ≤ n ≤ 9)态,随着主量子数 Table 1. Fine structure splittings of 1s2nd (n ≤ 9) states for Ni25+ ion (in cm−1) 表1. Ni25+ 离子的 1s2nd (n ≤ 9)的精细结构 StateRelativisticQED corr.Higher rel. Total Exp.[5] 1s23d16464.545638.3093 103.2870 16606.141916,600 1s24d6942.3338 16.1613 48.8460 7007.3412 7010 1s25d3553.6118 8.2741 25.3419 3587.2278 3590 1s26d2056.1844 4.7880 14.4833 2075.4557 1s27d1294.7517 3.0150 8.9429 1306.7096 1s28d867.3019 2.0198 5.8665 875.1883 1s29d607.9640 1.4186 4.0379 613.4206 Copyright © 2013 Hanspub 66 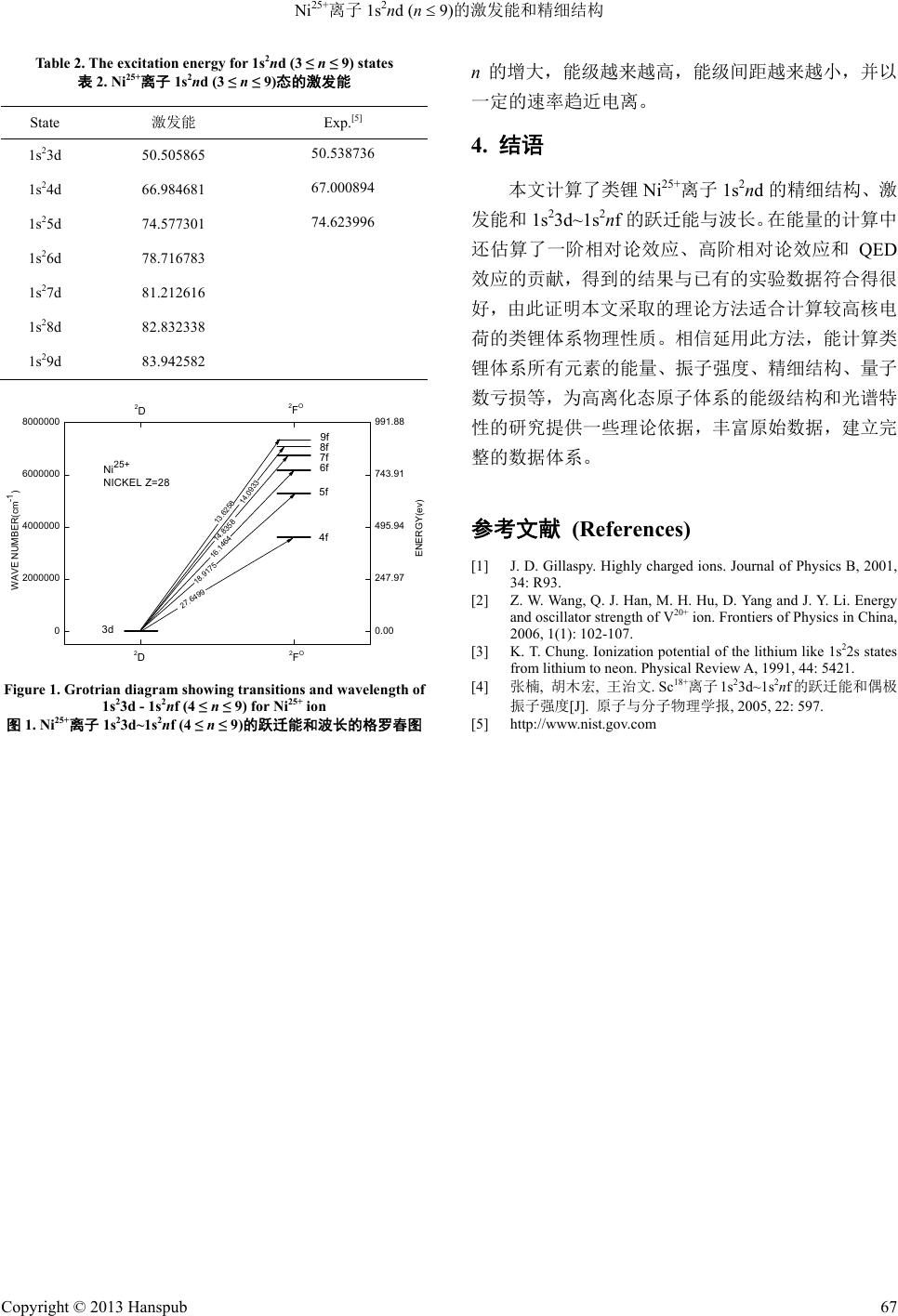 Ni25+离子 1s2nd (n 9)的激发能和精细结构 Copyright © 2013 Hanspub 67 Table 2. The excitation energy for 1s2nd (3 ≤ n ≤ 9) states n的增大,能级越来越高,能级间距越来越小,并以 一定的速率趋近电离。 表2. Ni25+离子 1s2nd (3 ≤ n ≤ 9)态的激发能 State 激发能 Exp.[5] 1s23d 50.505865 50.538736 1s24d 66.984681 67.000894 1s25d 74.577301 74.623996 1s26d 78.716783 1s27d 81.212616 1s28d 82.832338 1s29d 83.942582 4. 结语 本文计算了类锂Ni25+离子 1s2nd的精细结构、激 发能和 1s23d~1s2nf的跃迁能与波长。在能量的计算中 还估算了一阶相对论效应、高阶相对论效应和 QED 效应的贡献,得到的结果与已有的实验数据符合得很 好,由此证明本文采取的理论方法适合计算较高核电 荷的类锂体系物理性质。相信延用此方法,能计算类 锂体系所有元素的能量、振子强度、精细结构、量子 数亏损等,为高离化态原子体系的能级结构和光谱特 性的研究提供一些理论依据,丰富原始数据,建立完 整的数据体系。 0 2000000 4000000 6000000 8000000 0.00 247.97 495.94 743.91 991.88 9f 8f 7f 6f 5f 4f 2FO 2D ENERGY(ev) 13.6258 14.0933 14.8358 16.1464 18.9175 WAVE NUMBER(cm-1) 27.6499 Ni25+ NICKEL Z=28 2D2FO 3d 参考文献 (References) [1] J. D. Gillaspy. Highly charged ions. Journal of Physics B, 2001, 34: R93. [2] Z. W. Wang, Q. J. Han, M. H. Hu, D. Yang and J. Y. Li. Energy and oscillator strength of V20+ ion. Frontiers of Physics in China, 2006, 1(1): 102-107. [3] K. T. Chung. Ionization potential of the lithium like 1s22s states from lithium to neon. Physical Review A, 1991, 44: 5421. [4] 张楠, 胡木宏, 王治文. Sc18+离子 1s23d~1s2nf的跃迁能和偶极 振子强度[J]. 原子与分子物理学报, 2005, 22: 597. Figure 1. Grotrian diagram showing transitions and wavelength of 1s23d - 1s2nf (4 ≤ n ≤ 9) for Ni25+ ion 图1. Ni25+离子 1s23d~1s2nf (4 ≤ n ≤ 9)的跃迁能和波长的格罗春图 [5] http://www.nist.gov.com |