Finance
Vol.
09
No.
06
(
2019
), Article ID:
33097
,
16
pages
10.12677/FIN.2019.96073
Research on the Optimal Income Model of VC and Entrepreneurial Enterprises from the Perspective of Synergy Effect
Xiaoqing Yu
Donghua University, Shanghai

Received: Oct. 30th, 2019; accepted: Nov. 15th, 2019; published: Nov. 22nd, 2019

ABSTRACT
Based on C-D production function and synergy effect between VC and entrepreneur, this article mainly discusses four differential game models in the continuous time, which is namely cooperative game model, non-cooperative one, VC-dominating Stackelberg model, entrepreneur-dominating Stackelberg model. HJB equation is used to find the optimal return strategy. It analyses the effect on different VC shareholding ratios to the optimal return and synergy incentives. Matlab 7.0 is used to draft the relationship between relative parameters and optimal return strategy. Sensitivity analysis of model parameters is performed. The results show that entrepreneurs are more inclined to provide synergy incentives and bring higher total return when VC shareholding ratio is less than 50%; while it is greater than 50%, VC is more inclined to provide synergy incentives and bring higher total return.
Keywords:Synergy Effect, Venture Capital, HJB Equation
协同效应视角下VC与创业企业的最优收益模型研究
余小青
东华大学,上海

收稿日期:2019年10月30日;录用日期:2019年11月15日;发布日期:2019年11月22日

摘 要
运用C-D生产函数,基于VC与创业企业间的协同效应构建了连续时间下VC和创业企业协同合作、不合作、VC主导的Stackelberg主从博弈、创业企业主导的Stackelberg主从博弈微分收益模型,利用HJB方程求出了四种博弈模型下的最优收益策略,比较了VC不同的持股比例对最优收益、协同效应激励的影响,运用Matlab7.0作出各参数与最优收益策略的关系图并进行了参数的敏感性分析。结果表明,VC持股比例小于50%时,创业企业更倾向于提供协同效应激励,且此时会带来更高的创业链总收益;而VC持股比例大于50%时,VC更倾向于提供协同效应激励并带来更高的创业链总收益。
关键词 :协同效应,创业投资,HJB方程

Copyright © 2019 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
创业投资(venture capital,简称VC)是指通过向具有高成长性的创业企业提供股权资本,并为其提供管理和经营服务,期望在企业发展到相对成熟后,通过股权转让收取高额中长期收益的积极的投资行为 [1]。创业投资的投资对象是科技型的高成长性初创企业。王茵田等 [2] 提出由于初创企业难以满足银行贷款条件及上市要求而更偏好于股权融资。
信息不对称从时间上可分为事前信息不对称和事后信息不对称。逆向选择主要在签订合同之前发生,而道德风险则在合同签订之后发生。创业投资的当事人主要有投资者、创业投资机构、创业企业。三者之间衍生出投资者与创业投资机构之间、创业投资机构与创业企业之间的两重委托代理关系。当每个参与人都采取了对方观测不到的行动,并且影响到双方的利益时,此时的道德风险演化成为双边道德风险。金永红等 [3] 基于VC与初创企业的逆向选择问题设计了拥有不同能力企业家的最优分离均衡契约模型。王雁茜 [4] 用数学模型和供求曲线深入研究了风险投资过程中的逆向选择和道德风险问题。Ramy & Gaivious [5] 构建了风险投资家与风险企业家间的多阶段博弈模型,研究了双方订立合约时的道德风险问题,得出了最优的合约形式及最佳风险投资退出时机。Reid J. D. [6] 研究农地承租契约机制,首次提出双重道德风险问题。Casamatta [7] 在双重道德风险下,构建了VC、纯金融机构及创业企业间的委托代理模型。Hellmann [8] 研究双重道德风险下最优合约设计问题时发现与IPO相比,收购退出可以给VC带来更多流动性。吴萌 [9] 建立了包含公平偏好的多阶段行为激励模型防范道德风险模型。Geronikolaou [10] 研究了双重道德风险下竞争的加剧使得风险投资者更愿意投资那些处于早期阶段的项目。
创业投资家通过股权投资的方式向创业企业家注资并在合作过程中向初创企业提供管理培训、战略咨询等增值服务 [11]。创业企业接受创业投资企业的资本投资及增值服务时,会发生两方面的协同效应:一是成本节约的协同效应,即协同效应促成成本节约进而带来创业链总收益的增加。另一方面是收入的协同效应,即协同效应本身会促进创业链总收益的提高。Gorman & Sahlman [12] 指出VC所提供的咨询服务是商业成功的关键因素。Casamatta [7] 阐述了企业家虽有技术优势但缺乏商业经验,需要VC商业咨询方面的协助。党兴华等 [13] 从VC角度提出监控机制与激励约束合同具有替代性,从创业企业家角度提出监控与激励约束具有互补性。池仁勇 [14] 经研究发现VC、创投协会、供应商等创业链网络上的参与者在资源能力与战略利益方面的互补往往可产生创新溢出效应,形成良好的协同效应。Fairchild [15] 也指出企业家的能力与创业投资家经验之间所形成的互补产生了协同效应。Marcos Vergara等 [16] 强调了VC与EN之间的互补效应的重要性以及双方的互补效应如何影响双方的股权配置比例。
综上所述,基于连续时间的创业投资机构与创业企业间动态博弈建立双方及整个创业项目的微分收益模型。在赵黎明 [17] 基础上,创新性地运用了C-D产出函数,同时构建了VC和创业企业分别主导的Stackelberg主从博弈情形,进一步丰富了HJB方程在创业投资研究方面的应用。基于连续时间背景下VC和创业企业的动态博弈共构建了四种博弈模型,分别为完美信息条件下协同合作、不完全信息条件下不合作、不完全信息条件下由创业投资企业和创业企业分别主导的Stackelberg主从博弈情形,通过建立并求解HJB方程,得出了双方最优策略,即最优收益,最优努力水平,最优持股比例,最优协同效应激励因子,分析了创业投资不同的持股比例范围内最优收益的比较,不同持股比例范围内由谁提供协同效应激励能够带来更大的收益,并进一步应用了Matlab 7.0仿真软件,对得出的命题进行了数值仿真模拟,仿真结果与所提出的命题一致,进一步验证了命题。
2. 模型相关说明
2.1. 模型相关变量
基于合作博弈、不合作博弈、VC主导和创业企业主导的Stackelberg博弈分别构建了整个创业链、VC及创业企业的收益模型,引入协同效应激励因子,运用C-D生产函数,通过建立并求解HJB方程得出最优策略。模型中的相关变量,见表1。
Table 1. The main variables of the model
表1. 模型主要变量
2.2. 模型相关假设
假设1:创业企业与创业投资机构在资源、努力行为等方面存在互补性,从而会产生协同效应,协同效应带来了未来价值增值的潜力,这是双方进行合作的基础;
假设2:创业企业项目的控制权与收益分享权是可分离的。本文分别讨论创业企业与创业投资机构分别拥有创业企业项目控制权的条件下创业投资机构所获得最优收益的最优分配比例 ;
假设3:创业企业与创业投资机构的努力水平具有不可观测但可证实的特性;
假设4:创业投资机构与创业企业之间产生的协同效应促进了价值增值,从而带来的收益的提高。变量H (t)代表协同效应,采用如下随机微分方程来反应H (t)随时间的变化 [17]:
;
假设5:创业企业与创业投资机构之间产生的协同效应行为规模报酬不变。创业企业的产出函数为:
;
假设6:创业企业的努力成本 ,创业投资机构的努力成本 ,其中,
代表成本系数,且均大于零。
2.3. VC和创业企业协同的目标函数推导
整个创业投资过程中,创业企业与创业投资机构在时刻t的总收益为:
。
(1) VC提供协同效应激励的双方目标函数
创业投资家为促进协同效益对收益产生更大的作用,提供给创业企业家相应的“激励因子”(设为 且 )来激励企业家努力提高项目的收益,提高项目成功的概率。
创业投资机构的目标函数为:
。
创业企业的目标函数为:
。
整个创业链的目标函数为:
。
(2) 创业企业提供协同效应激励的双方目标函数
创业企业为促进协同效益给公司带来更大的收益,提供给创业投资企业相应的“激励因子”(设为 且 )来激励企业投资企业努力利用协同效应提高项目收益,同时增加项目成功的概率。
创业投资机构的目标函数为:
。
创业企业的目标函数为:
。
整个创业链的目标函数依然为:
。
3. 最优策略模型构建与求解
3.1. 完全信息条件下最优微分收益模型构建与求解
完全信息条件下,创业投资企业与创业企业之间的信息完全对称,即不存在任何一方利用信息优势获取额外利益,双方将从社会整体利益最大化的角度来选择各自的努力水平,虽然完全信息状态仅为一种理想状态,却成为了分析的可比状态。
定理1 完全信息条件下,双方协同合作时整个创业链的最优利润函数为:
。(1)
证明:完全信息条件下,VC与创业企业双方的目标一致,均以整体利益最大化为目标,双方的共同目标函数如下:
。
假设最优收益函数 满足如下的HJB方程:
。
上式对 和 求一阶导数后,并运用赵黎明(2016)方法求出整个创业链最优利润函数为:
,
定理1中(1)式得以证明。
3.2. VC和创业企业不合作的最优微分收益模型构建与求解
在不完全信息条件下,当创业企业与创业投资企业均无主动权,双方地位均等时,此时,双方将会以各自利益最大化为原则进行决策,根据理性的创业投资企业和创业企业都将不会向对方提供激励因子,因此, 。
定理2 在不完全信息双方地位对等条件下,创业投资企业、创业企业及整个创业链的最优利润函数分别为:
, (2)
, (3)
。 (4)
证明:为得到此博弈的古诺均衡解,首先,假设存在连续有界的微分收益函数 , 对所有的 都满足Hamilton-Jacobi-Bellman (HJB)方程:
,
, (5)
,
。 (6)
为使创业企业利益最大化,(5)式和(6)式分别对 , 求一阶偏导,
求得唯一一组符合条件的正实数解如下:
, (7)
。 (8)
将(5)式、(6)式再对H对一阶偏导后再与(7)式、(8)式联立得:
,(9)
。 (10)
与完全信息条件下协同合作最优策略解法相同,求得创业投资机构与创业企业的最优努力函数分别为:
,
。
整个创业链的最优利润函数为:
。
定理2中(2)式、(3)式、(4)式得以证明。
3.3. 不完全信息条件下VC Stackelberg博弈模型建立与求解
创业投资家先选择投资的资本以及给创业企业家的激励因子,创业企业家在观测到创业投资家的行动后,据总资本及激励要求制定相应的项目实施方案,此时,相当于在创业企业与创业投资机构之间建立了以创业投资企业为领导者而创业企业为追随者的Stackelberg主从博弈模型,通过逆向归纳法对模型进行分析,得出双方最优努力水平及最优收益函数,同时讨论了创业投资家的持股比例对于“激励因子”的影响。
定理3 在Stackelberg主从博弈模型下,创业投资企业提供给创业企业的最优激励因子为:
,其中, 。 (11)
创业投资企业和创业企业以及整个创业链的最优利润函数分别为:
, (12)
,(13)
。(14)
证明:采用逆向归纳法得到此博弈的Stackelberg均衡解,分别求出创业企业和创业投资机构的最优收益。创业企业的最优收益:
, (15)
(15)式对 求一阶导数,并令其等于零,可以求得:
。 (16)
创业投资企业预测到创业企业的努力水平反应式,于是创业投资机构将依据创业企业努力水平的反应函数来选择自己的最优努力水平。创业投资机构的HJB方程为:
。 (17)
将(16)式代入(17)式,并分别对 、 求一阶导。
数并令其等于零,得到创业投资企业和创业企业的最优努力水平以及最优激励因子,最终得到唯一一组符合条件的正实数解,即不完全信息条件下由创业投资企业主导型的博弈双方均衡时最优策略分别为:
创业投资企业与创业企业的最优努力水平策略分别为:
,
。
创业投资企业提供给创业企业的最优激励因子为:
,其中, 。
定理3中的(11)式得以证明。
创业投资企业和创业企业以及整个创业链的最优利润函数分别为:
,
,
。
定理3中的(12)式、(13)式、(14)式得以证明。
3.4. 不完全信息条件下创业企业主导型Stackelberg博弈模型建立与求解
创业企业先选择投资的资本,同时提供给创业投资企业的激励因子为 ,创业投资企业在观测到创业企业的行动后,据总资本及激励要求制定相应的项目实施方案,此时,相当于在创业企业与创业投资机构之间建立了以创业企业为领导者而创业投资机构为追随者的Stackelberg主从博弈模型,运用逆向归纳法分析模型,得出双方最优努力水平及最优收益函数,同时讨论了创业投资家的持股比例对于“激励因子”的影响。
定理4 在不完全信息条件下由创业企业主导型的Stackelberg博弈均衡时创业投资企业提供给创业企业的最优激励因子为:
,其中, 。 (18)
创业投资企业和创业企业以及整个创业链的最优利润函数分别为:
, (19)
, (20)
。 (21)
证明:采用逆向归纳法得到此博弈的Stackelberg均衡解,分别求出创业投资机构与创业企业的最优收益。创业投资企业的最优收益为:
。 (22)
经求解得创业投资企业与创业企业的最优努力水平策略分别为:
,
。
创业投资企业提供给创业企业的最优激励因子为:
,其中, 。
定理4中的(18)式得以证明。
创业投资企业和创业企业以及整个创业链的最优利润函数分别为:
,
,
。
定理4中的(19)式、(20)式、(21)式得以证明。
4. 博弈均衡结果比较分析
定理5 对任意的 ,创业投资企业、创业企业及创业链整体的最优利润的排序如下:
(1)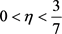 时,
时,
① 创业投资企业的最优利润排序为:
;
② 创业企业的最优利润排序如下:
;
③ 整个创业链的最优利润排序如下:
;
(2) 时,
① 创业投资企业的最优利润排序为:
;
② 创业企业的最优利润排序如下:
;
③ 整个创业链的最优利润排序如下:
时, ;
时, ;
(3) 时,
① 创业投资企业的最优利润排序为:
;
② 创业企业的最优利润排序如下:
;
③ 整个创业链的最优利润排序如下:
;
证明:
创业投资企业最优利润排序证明如下:
时,
;
所以, 。其他情形下同理可证。
5. 数值仿真分析
模型中参数的选择影响着创业投资企业、创业企业最优努力水平、最优利润水平以及创业链整体的最优利润水平。我们模型中的大部分参数参照赵黎明(2016) [17] 中的取值,模型中的贴现率取 ,协同效应衰减因子 ,,, ;除此之外,我们设C-D生产函数前的系数 ,。
协同合作情形下的协同效应为 ,当 时, ,创业链最优总收益
为 ;VC与创业企业非合作情形下,协同效应 ,创业链最优总收益为 ,创业投资企业的最优收益为 ,创业企业的最优收益为 ;VC主导型主从博弈情形下,协同效应
,创业链最优总收益为 ,创业投资企业的最优收益为 ,创业企业的最优收益为 ;创业企业主导型主从博弈情形下,协同效应 ,创业链最优总收益为 ,创业投资企业的最优收益为 ,创业企业的最优收益为 。
5.1. 不同博弈情形下VC持股比例与最优收益的对比分析
见图1,
代表合作条件下整个创业链的最优总收益;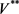 、
、
分别表示非合作条件下创业链最优总收益、创业投资企业最优收益、创业企业最优收益;
、
、
分别表示由创业投资企业主导的Stackelberg博弈情形下创业链最优总收益、创业投资企业最优收益、创业企业最优收益;
、
、
分别表示由创业企业主导的Stackelberg博弈情形下创业链最优总收益、创业投资企业最优收益、创业企业最优收益。
、
、
分别表示非合作条件下创业链最优总收益、创业投资企业最优收益、创业企业最优收益;
、
、
分别表示由创业投资企业主导的Stackelberg博弈情形下创业链最优总收益、创业投资企业最优收益、创业企业最优收益;
、
、
分别表示由创业企业主导的Stackelberg博弈情形下创业链最优总收益、创业投资企业最优收益、创业企业最优收益。
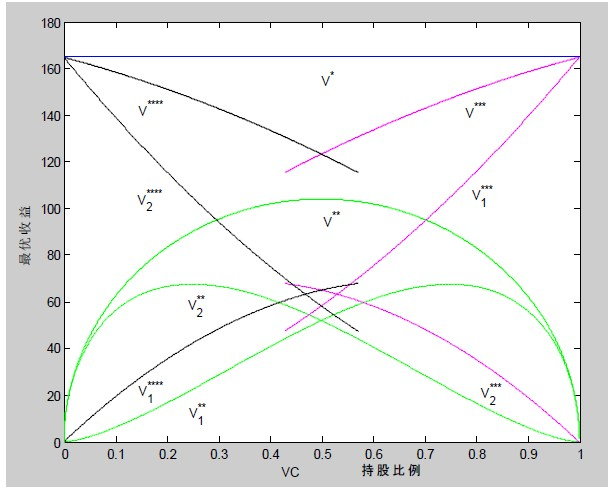
Figure 1. The comparative analysis of VC shareholding ratio and optimal returns in different game situations when t = 10
图1. t = 10时,不同博弈情形下VC持股比例与最优收益的对比分析
从图1可看出,不论VC持股比例如变化,不合作情形下的创业链最优总收益始终最低,合作情形下创业链总收益始终最高,且不受VC持股比例水平的影响,Stackelberg主从博弈情形下的创业链收益介于二者之间。
比较创业链总收益后,接着来比较不同情形下创业投资企业与创业企业各自的最优收益。如图所示,在非合作情形下,在VC持股比例小于50%时,创业企业的最优收益更高;而一旦VC持比例超过50%时,创业投资企业将获得更高的最优收益;当VC持股比例等于50%时,创业投资企业和创业企业的最优收益相同,均分享创业链总收益的一半利润。
由创业企业主导的Stackelberg主从博弈情形下,在VC持股比例小于50%时,创业企业将分享更多
的创业链收益,而VC持股比例介于 时创业投资企业将分享更多的创业链收益。由创业投资企业主导的Stackelberg主从博弈情形下,在VC持股比例介于 时,创业企业将分享更多的创业
链收益,而VC持股比例大于50%时创业投资企业将分享更多的创业链收益。
进一步我们可以分析,Stackelberg主从博弈情形下,当VC持股比例处于交叉区域即 时,
双方均愿为对方提供协同效应“激励因子”,但考虑到经济资源的有效配置,我们建议VC持股比例
,由创业企业为创业投资企业提供协同效应“激励因子”;而VC持股比例 ,由创
业投资企业为创业企业提供协同效应“激励因子”。
因为在Stackelberg主从博弈情形下,创业链总收益的角度与双方各自利益在这段交叉区域内并不冲突,反而达到了完美的相一致,从而有利于双方更好地决定协同效应“激励因子”的提供方。具体来说,
当VC持股比例 ,创业企业将更有动力提供协同效应“激励因子”时,创业链总收益要更大,同时创业企业的最优利润将高于创业投资企业;而当VC持股比例 ,创业投资企业更有动力提
供协同效应“激励因子”时,创业链总收益要更大,同时创业投资企业的最优利润将高于创业投资企业。
5.2. 持股比例对最优激励因子的影响分析
(1) 在不完全信息条件下由创业投资主导型的Stackelberg博弈均衡时,创业投资企业提供给创业企业的最优激励因子为:
,其中, 。
见图2,由创业投资企业主导型的主从博弈中,随着VC持股比例的增加,VC给创业企业提供的协同效应激励因子也不断增加,虽然增加的速率在递减,但总趋势是向上的。
Figure 2. The relationship between the optimal incentive factor and VC shareholding ratio in VC-dominated master-slave game
图2. VC主导型主从博弈下最优激励因子与VC持股比例的关系
(2) 在不完全信息条件下由创业企业主导型的Stackelberg博弈均衡时,创业企业提供给创业投资企业的最优激励因子为:
,其中, 。
见图3,随着创业投资企业持股比例的提高,创业企业提供给创业投资企业的激励因子以递增的速度在下降。这表明,创业企业本身并不倾向于提供激励因子,而是出于某些特殊的目的需要,一旦目的逐渐接近目标,那么,提供协同激励的动力也将迅速减弱。项目早期融资需求大,所以,需要给予更多的激励;随着项目越来越成熟,项目变得越来越有吸引力,会加速减少激励因子,甚至在VC持股比例
达到 时,创业企业提供给VC的激励因子减少至零。所以,相比于VC,创业企业在VC持股比例较高
时提供激励因子的意愿相对较弱。
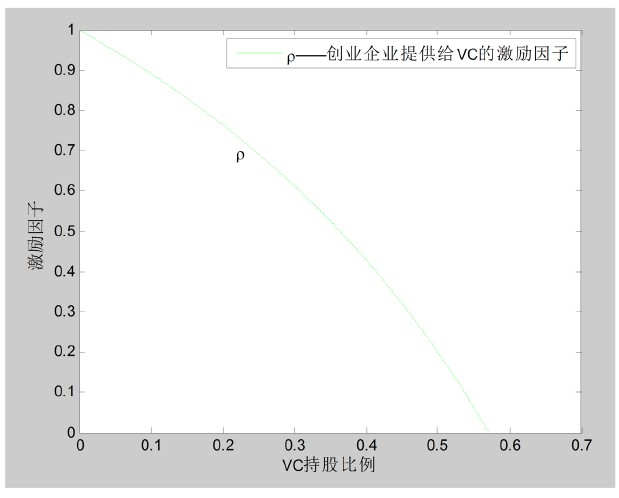
Figure 3. The relationship between the optimal incentive factor and VC shareholding ratio in the entrepreneurial enterprise-dominated master-slave game
图3. 创业企业主导型主从博弈下最优激励因子与VC持股比例的关系
(3) 时,VC与创业企业激励因子的对比分析
创业投资企业提供给创业企业的最优激励因子为: 。
创业企业提供给创业投资企业的最优激励因子为: 。
见图4,在 时,VC和创业企业提供给对方的激励因子相等;当 时,创业企业提供的激励因子要大于VC提供的激励因子,这与前期的融资需求紧密相关,直至 后,VC提供的激励因子超过了创业企业提供的激励因子。

Figure 4. The relationship between the optimal incentive factor and VC shareholding ratio when
图4. 时最优激励因子与VC持股比例的关系
6. 结论
利用微分对策理论研究了创业投资与创业企业的最优收益策略,基于协同效应构造了创业链、创业投资企业、创业企业的目标收益函数,并运用HJB方程求出了四种博弈情形下的最优策略。
协同合作情形下,创业链整体的收益始终最高,且不受VC持股比例水平的影响;而非合作情形下的创业链总收益最低,且随着VC持股比例的增加,创业链总收益以递减的速率不断增加,直至VC持股比率达到50%时,创业链总收益达到最大值,VC持股比例超过50%时,非合作的创业链总收益随持股比例的持续增加而下降。由创业企业主导的Stackelberg主从博弈情形下,随着VC持股比例的增加,
创业链总收益在不断下降,创业投资企业最多只愿意提供 的持股比例;由创业投资企业主导的Stackelberg主从博弈情形下,一般VC持股比例会大于 ,且随着VC持股比例地继续增加,创业链的
总收益会不断提升。
在VC持股比例 时,VC和创业企业提供给对方的激励因子相等;当 时,创业企业提供的激励因子要大于VC提供的激励因子,这与前期的融资需求紧密相关,表明创业企业吸引资本的激励要大于VC促进项目成功的激励,项目早期VC有对创业企业进行筛选的权力,随着VC持股比例的逐渐提高,VC越来越关注项目的成功可能性,因此,提供的激励因子逐渐增加,直至 后,VC提供的激励因子超过了创业企业提供的激励因子,而且两激励因子差值越来越大,一方面因为创业企业的融资需求小于项目早期,且项目风险也小于早期,所以,创业企业提供的激励因子越来越小;另一方面,创业投资企业VC的大量资本注入,资本权重的加大,越来越看重项目的成败,所以,VC提供的激励因子越来越大。综上所述, 时,创业企业更倾向于提供协同效应激励因子; 时,创业投资企业VC更倾向于提供协同效应激励因子。
在VC持股比例相对较低时, 时,无论是协同合作、不合作、还是Stackelberg主从博弈情形,创业企业都将从创业链中获得更高的最优收益;而在VC持股比例相对较高时, 时,无论
哪种博弈情形,创业投资企业都将从创业链中获得更高的最优收益。除此之外,当VC持股比例处于交
叉区域,即 时,双方收益的高低取决于由谁提供协同效应“激励因子”,VC持股比例 时,由创业企业提供协同效应“激励因子”将会使资源得到更有效应的利用;VC持股比例 时,由创业投资企业提供协同效应“激励因子”将会使资源得到更有效应的利用。
虽然文章主体部分是有关理论推导,并包含多个假设,但结果却具有实际意义。VC与创业企业协同的最优策略研究有利于VC与创业企业更好地理解双方合作过程中的协同效应及相应的激励措施度的把握,尽管可能会存在一定程度的冲突,但双方整体创业链的目标还是一致。文章的局限在于为求博弈模型的解析解,简化了相关参数。后续研究中生产函数方面有改进的空间,如将C-D生产函数替换成应用更广泛的CES生产函数等;文章重点研究了VC与创业企业间的道德风险问题,未来可再进行延伸,加入创业投资者与创业投资机构,创业投资机构与创业间的双重道德风险进行研究。这些问题都有待于将来进行深入研究。
文章引用
余小青. 协同效应视角下VC与创业企业的最优收益模型研究
Research on the Optimal Income Model of VC and Entrepreneurial Enterprises from the Perspective of Synergy Effect[J]. 金融, 2019, 09(06): 657-672. https://doi.org/10.12677/FIN.2019.96073
参考文献
- 1. 张帏, 姜彦福, 陈耀刚. 风险投资中的代理问题、风险分担与制度安排[J]. 科研管理, 2002, 23(1): 122-127.
- 2. 王茵田, 黄张凯, 陈梦. “不平等条约?”: 我国对赌协议的风险因素分析[J]. 金融研究, 2017(8): 117-128.
- 3. 金永红, 奚玉芹, 叶中行. 风险投资中的逆向选择: 分离均衡式契约安排[J]. 系统工程学报, 2002, 17(6): 556-561.
- 4. 王雁茜, 周启功. 风险投资投资过程的逆向选择和道德风险[J]. 科研管理, 2002, 23(3): 105-111.
- 5. Elitzur, R. and Gavious, A. (2003) A Multi-Period Game Theoretic Model of Venture Capitalists and Entrepreneurs. European Journal of Operational Research, 144, 440-453. https://doi.org/10.1016/S0377-2217(02)00144-3
- 6. Reid, J.D. (1977) The Theory of Share Tenancy Revisited-again. Journal of Political Economy, 85, 403-407. https://doi.org/10.1086/260571
- 7. Casamatta, C. (2003) Financing and Advising: Optimal Financial Contracts with Venture Capitalists. The Journal of Finance, 58, 2059-2086. https://doi.org/10.1111/1540-6261.00597
- 8. Hellmann, T. (2006) IPOs, Acquisition and the Use of Convertible Securities in Venture Capital. Journal of Financial Economics, 81, 649-679. https://doi.org/10.1016/j.jfineco.2005.06.007
- 9. 吴萌. 风险企业家考虑公平关切的风险投资多阶段激励模型[J]. 管理工程学报, 2016, 30(3): 72-80.
- 10. Geronikolaou, G. and Papachristou, G. (2016) Investor Competition and Project Risk in Venture Capital Investments. Economics Letters, 141, 67-69. https://doi.org/10.1016/j.econlet.2016.02.007
- 11. 薛力, 郭菊娥. 风险投资机构内部融资模式对风险投资家股权投资策略的影响[J]. 系统管理学报, 2018, 27(2): 201-207.
- 12. Gorman, M. and Sahlman, W.A. (1989) What Do Venture Capitals Do? Journal of Business Venturing, 4, 231-248. https://doi.org/10.1016/0883-9026(89)90014-1
- 13. 党兴华, 权小锋, 杨敏利. 风险投资委托代理关系中的监控与激励博弈分析[J]. 科研管理, 2007, 28(1): 155-160.
- 14. 池仁勇. 区域中小企业创新网络的结点联结及其效率评价研究[J]. 管理世界, 2007(1): 105-112.
- 15. Fairchild, R. (2011) An Entrepreneur’s Choice of Venture Capitalist or Angel Financing: A Behavioral Game-Theoretic Approach. Journal of Business Venturing, 26, 359-374. https://doi.org/10.1016/j.jbusvent.2009.09.003
- 16. Vergara, M., Bonilla, C.A. and Sepulveda, J.P. (2016) The Com-plementarity Effect: Effort and Sharing in the Entrepreneur and Venture Capital Contract. European Journal of Operational Research, 254, 1017-1025. https://doi.org/10.1016/j.ejor.2016.04.040
- 17. 赵黎明. 基于创业链声誉的风险投资与风险企业合作的微分对策模型[J]. 管理工程学报, 2016, 30(1): 169-175.
