Pure Mathematics
Vol.06 No.01(2016), Article ID:16868,7
pages
10.12677/PM.2016.61012
A Limit Property for Non-Homogeneous Markov Chain in Markov Environments
Cheng Cheng
School of Mathematics Physics Science and Engineering, Anhui University of Technology, MaAnshan Anhui

Received: Nov. 6th, 2015; accepted: Jan. 26th, 2016; published: Jan. 29th, 2016
Copyright © 2016 by author and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
In this paper we discuss the strong limit properties for moving average of functions of non-ho- mogeneous Markov chain in Markov environments. By constructing a sequence of random variables with one parameter and take 1 as the expectation, with the aid of the classic Borel-Cantelli lemma, we study the strong limit properties of Markov chain in random environments and obtain a strong limit theorem for moving average of functions of non-homogeneous Markov chain in Markov environments. Moreover, we generalize the existing results.
Keywords:Markov Chain, Markov Environments, Strong Limit Theorem, Relative Entropy

关于马氏环境中马氏链的一个极限性质
程成
安徽工业大学数理科学与工程学院,安徽 马鞍山

收稿日期:2015年11月6日;录用日期:2016年1月26日;发布日期:2016年1月29日

摘 要
本文研究马氏环境中非齐次马氏链泛函的滑动平均强极限性质。通过构造一列带参数且期望为1的随机变量,利用Borel-Cantelli引理来研究随机环境中马氏链的强极限定理,得到了马氏环境中马氏链泛函滑动平均的一个强极限定理,推广了若干已有结论。
关键词 :马氏链,马氏环境,强极限定理,相对熵

1. 引言与定义
马氏链的极限理论是随机过程中极其重要研究内容,关于这方面的研究成果十分丰富,但以往的研究主要集中在讨论确定环境下马氏链的随机行为,对随机环境中马氏链的研究是近几十年来随机过程理论中的一个新兴课题,也有不少深刻的结果。文献[1] -[3] 构造了一Hopf-链,并且利用Hopf-链理论研究了平稳环境中马氏链的遍历理论、中心极限定理、直接收敛与转移函数的周期性关系以及不变概率测度的存在性。文献 [4] 讨论了马氏环境中马氏链与马氏双链间的关系。文献 [5] 利用鞅差序列的理论研究了随机环境中的马氏链,在假设马氏双链遍历的条件下,得到了马氏环境中马氏链的强大数定理成立的充分条件。文献 [6] 讨论了随机环境中马氏链的大偏差问题。文献 [7] 通过对随机环境中马氏链的一般性构造性定义,在过程的矩满足适当的条件下,利用截尾方法和鞅收敛定理,得到随机环境中马氏链的一类泛函极限定理,文献 [8] [9] 利用鞅方法讨论了随机环境中非齐次马氏链的强大数定理。
最近汪忠志与杨卫国教授提出了一种研究随机序列滑动和强收敛性的新方法 [10] ,其要点是构造带参数的且期望为1的随机序列,然后利用经典的Borel-Cantelli引理来获得随机序列的强收敛性。受他们工作的启发,本文利用该方法来讨论马氏环境中马氏链,获得了马氏环境中马氏链泛函的一个强极限定理,将文献 [11] 中的相关结果推广到滑动平均情况。
设 表示整数集,
表示整数集, 表示非负整数集。
表示非负整数集。 是所考虑的一概率空间,令
是所考虑的一概率空间,令 ,
, ,
, 和
和 分别是定义在
分别是定义在 上取值于
上取值于 和
和 的随机序列,
的随机序列, 是
是 的一步转移函数族,
的一步转移函数族,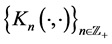 是
是 的一步转移函数族。
的一步转移函数族。
定义1.1 如果对任意 ,有
,有

及

则称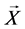 为随机环境
为随机环境 中马氏链,
中马氏链, 为随机环境序列;若
为随机环境序列;若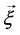 是一马氏序列,则称
是一马氏序列,则称 是马氏环境中马氏链。
是马氏环境中马氏链。
本文恒设 是马氏环境
是马氏环境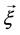 中的马氏链,其中
中的马氏链,其中 的一步转移函数为
的一步转移函数为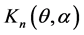 ,由文献 [4] [5] 知
,由文献 [4] [5] 知 是马氏双链,其初始分布和一步转移矩阵分别为
是马氏双链,其初始分布和一步转移矩阵分别为
 (1.1)
(1.1)
 (1.2)
(1.2)
其中 。令
。令 ,对
,对 ,
,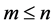 ,由马氏性,有
,由马氏性,有
 ,(1.3)
,(1.3)
定义1.2 设 定义如前,
定义如前, 是一列取正整数值序列,令
是一列取正整数值序列,令
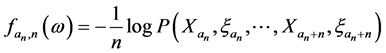
 称为
称为 的广义相对熵密度,由式(1.3),有
的广义相对熵密度,由式(1.3),有
 (1.4)
(1.4)
注:若令 ,则
,则 就是[9] 中定义的经典的相对熵密度。
就是[9] 中定义的经典的相对熵密度。
引理1.1 [11] 设 是一列正的随机变量且满足
是一列正的随机变量且满足 ,则
,则
 (1.5)
(1.5)
2. 主要结论
定理2.1 设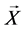 是马氏环境
是马氏环境 中的马氏链,其中
中的马氏链,其中 的一步转移函数为
的一步转移函数为 ,
, 的一步转移函数为
的一步转移函数为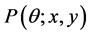 ,
, 是定义在
是定义在 上的一列四元实值函数。如果存在一个常数
上的一列四元实值函数。如果存在一个常数 ,使得对任意
,使得对任意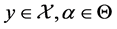 有
有
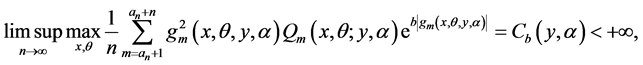 (2.1)
(2.1)
则
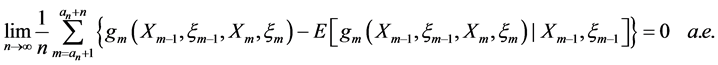 (2.2)
(2.2)
证明:为了以下证明的需要,我们先来构造一个辅助随机函数。设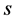 为非零常数,
为非零常数, 为固定的状态。简记
为固定的状态。简记 ,
, 分别为
分别为 和
和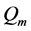 。令
。令
 (2.3)
(2.3)
注意到

(马氏性)
其中 ,
,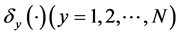 是Kronecker函数。
是Kronecker函数。
又

归纳地,可得
 (2.4)
(2.4)
由引理1.1以及(2.4),有 ,即存在
,即存在 ,使得
,使得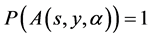 且
且
 。 (2.5)
。 (2.5)
由(2.3)有
 (2.6)
(2.6)
由式(2.5)及(2.6),有
 。 (2.7)
。 (2.7)
设 ,将(2.7)式两边同除以
,将(2.7)式两边同除以 ,得
,得
 (2.8)
(2.8)
由(2.8)与上极限性质

及不等式

有
 (2.9)
(2.9)
当 时,由(2.1)及(2.9),有
时,由(2.1)及(2.9),有
 (2.10)
(2.10)
取 ,使
,使 ,并令
,并令 ,则对所有的
,则对所有的 ,由(2.10),有
,由(2.10),有
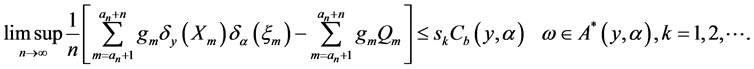 (2.11)
(2.11)
由于 ,故由式(2.11),有
,故由式(2.11),有
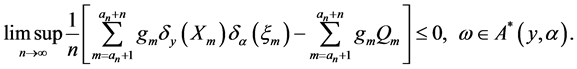 (2.12)
(2.12)
设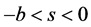 ,在(2.7)两边同除以
,在(2.7)两边同除以 ,类似地对下确界相应地由(2.8)~(2.10),同理可得
,类似地对下确界相应地由(2.8)~(2.10),同理可得
 (2.13)
(2.13)
取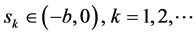 ,使
,使 ,并令
,并令 ,则对所有的
,则对所有的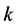 ,由(2.13),有
,由(2.13),有
 (2.14)
(2.14)
由于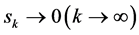 ,故由(2.14),有
,故由(2.14),有
 (2.15)
(2.15)
令 ,由(2.12),(2.15)有
,由(2.12),(2.15)有
 (2.16)
(2.16)
令 ,注意到
,注意到
 (2.17)
(2.17)
由于 ,故由(2.16),(2.17)知(2.2)成立。证毕。
,故由(2.16),(2.17)知(2.2)成立。证毕。
作为定理2.1的推论,推论2.2给出了马氏环境中马氏信源广义相对熵密度的一个极限定理,推论2.3给出了关于任意马氏环境中马氏信源均成立的一个极限结果。
推论2.2设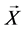 是马氏环境
是马氏环境 中的马氏链,其中
中的马氏链,其中 的一步转移函数为
的一步转移函数为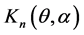 ,
,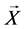 的一步转移函数为
的一步转移函数为 ,
, 是由式(1.4)定义的相对熵密度,则有
是由式(1.4)定义的相对熵密度,则有
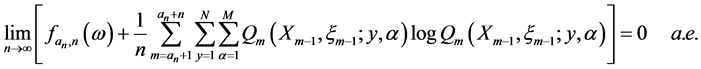 (2.18)
(2.18)
证明:由于 ,由引理1.1,得
,由引理1.1,得
 (2.19)
(2.19)
在定理2.1中令 ,则有
,则有
 (2.20)
(2.20)
由不等式 ,对任意的
,对任意的 ,有
,有
 (2.21)
(2.21)
由(2.19),(2.20)和(2.21)及定理2.1知推论成立。证毕。
推论2.3 设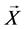 是马氏环境
是马氏环境 中的马氏链,
中的马氏链, 表示序列
表示序列 中
中 出现的次数,即
出现的次数,即
 (2.22)
(2.22)
则
 (2.23)
(2.23)
证明: 对固定的 ,在定理2.1中令
,在定理2.1中令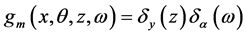 ,
, ,则有
,则有
 (2.24)
(2.24)
易知 满足条件(2.1),故由定理2.1与(2.24),知推论成立。证毕。
满足条件(2.1),故由定理2.1与(2.24),知推论成立。证毕。
基金项目
安徽省自然科学基金(1408085MA04),安徽工业大学研究生创新研究基金(2014132)。
文章引用
程 成. 关于马氏环境中马氏链的一个极限性质
A Limit Property for Non-Homogeneous Markov Chain in Markov Environments[J]. 理论数学, 2016, 06(01): 81-87. http://dx.doi.org/10.12677/PM.2016.61012
参考文献 (References)
- 1. Cogburn, R. (1984) The Ergodic Theory of Markov Chains in Random Environments. Z.W., 66, 109-128.
- 2. Cogburn, R. (1990) On Direct Convergence and Periodicity for Transition Probabilities of Markov Chains in Random Environments. Annals of Probability, 18, 642-654. http://dx.doi.org/10.1214/aop/1176990850
- 3. Cogburn, R. (1991) On the Central Limit Theorem for Markov Chains in Random Environments. Annals of Probability, 19, 587-604. http://dx.doi.org/10.1214/aop/1176990442
- 4. 李应求. 关于马氏环境中马氏链的几点注记[J]. 数学发展, 1999, 28(4): 358-360.
- 5. 李应求. 状态可数的马氏环境中马氏链函数的强大数定律[M]. 数学杂志, 2003, 23(4): 484-490.
- 6. Seppalainen, T. (1994) Large Deviations for Markov Chains with Random Transitions. Annals of Probability, 22, 713- 748. http://dx.doi.org/10.1214/aop/1176988727
- 7. 毕秋香, 李炜. 随机环境中马氏链的泛函极限定理[J]. 中山大学学报, 2000, 39(6): 153-156.
- 8. 汪忠志, 陈文波. 随机环境中非齐次马氏链的一类强极限定理[J]. 河南科学, 2002, 20(4): 336-338.
- 9. 汪忠志. 随机环境中非齐次马氏链泛函的一类强极限定理[J]. 安徽工业大学学报, 2004, 21(1): 79-82.
- 10. Wang, Z.Z. and Yang, W.G. (2015) The Generalized Entropy Ergodicity Theorem for Nonhomogeneous Markov Chains. Journal of Theoretical Probability, 1-15. http://dx.doi.org/10.1007/s10959-015-0597-9
- 11. 李应求. 马氏环境中马氏链的一类强极限定理[J]. 数学进展, 2008, 37(5): 539-549.