Pure Mathematics
Vol.
09
No.
01
(
2019
), Article ID:
28661
,
9
pages
10.12677/PM.2019.91012
Empirical Likelihood Statistic Inference for Distribution Function for PA Dependent Samples
Juan Huang
School of Mathematics and Computer, Guangdong Ocean University, Zhanjiang Guangdong

Received: Jan. 2nd, 2019; accepted: Jan. 21st, 2019; published: Jan. 28th, 2019

ABSTRACT
This paper studies distribution function by group empirical likelihood method under strongly stationary PA random sample. And we develop empirical likelihood ratio method to construct approximate confidence regions for distribution function.
Keywords:Positive Associate, Group Empirical Likelihood, Confidence Intervals
正相协相依样本下分布函数的经验似然统计 推断
黄娟
广东海洋大学,数学与计算机学院,广东 湛江

收稿日期:2019年1月2日;录用日期:2019年1月21日;发布日期:2019年1月28日

摘 要
本文将在正相协相依样本下,利用分组经验似然比方法,构造分布函数的置信区间。
关键词 :正相协,分组经验似然,置信区间

Copyright © 2019 by author and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
Joag-Dey和Proschan (1983, [1] )提出了PA (positive associate)随机变量在可靠性理论和多元统计分析中有广泛的应用。经验似然是由Owen (1988)提出的一种非参数推断方法 [2] [3] ,其有类似Bootstrap的抽样特性。这一方法与传统的统计方法比较有很多优点。比如:用经验似然方法构造置信区间拥有域保持性,变换不变性,置信域的形状由数据自行决定,以及Bartlett纠偏性和无需构造轴统计量等等。因而在相依情形下,经验似然方法研究成果少见 [4] - [10] ,尤其在PA相依样本见之甚少。目前,关于分布函数的研究多数局限于非参数核方法。本文将尝试在PA相依样本下,攻克普通经验似然方法的缺陷,重新利用分组经验似然方法,构造未知的分布函数置信区间。首先给出PA序列概念。
定义1: [1] 称随机变量
(
)是PA的,如果对于集合
的任何两个不相交的非空子集
和
,都有
此处,
与
是任何两个使得协方差存在的对每个变量均非降(或非升)的函数。称随机变量序列
是PA序列,如果对任何
,随机变量
(
)都是PA (正相协)的。
若
为来自总体
的正相协样本,由于
,
经验似然
对数经验似然为
。
此处
,且满足
。
2. 主要的结论及其证明
条件:
1)
是来自总体的强平稳PA样本;
2) 令
,若对某个
,满足
,
3)
;
定理1:如果上述条件成立,我们有
。
此处
,
。
然而
和
未知,定理1的结果不能应用,为了攻克这一缺陷,下面利用分组经验似然方法,重新构造经验似然比函数。
记
,其中
表示取整,
为简单起见,使
。
令
(对任意的
)
由于
的强平稳性,
有共同分布函数
,对应经验分布函数
。分组经验似然比为
。
对数经验似然比为
。
此处
且满足
。
定理2:在定理1的条件下,我们有
,
。
利用定理2,当样本
比较大时,可构造未知的分布函数
的置信水平为
的渐近置信区域:
,其中
为
分布的上
分位点,例如
取0.05或0.01。
引理1:记
,有
。
证明:由于
有界,易得
。
引理2: [7] 若
为PA变量,有
,且
,
。令
,
,假设对某个
,
,则
。
引理3: [11] 设
是强平稳PA序列,并且
,假定
,
,则
收敛,且有
,其中
为标准正态分布。
引理4:设
是强平稳PA序列,则有
。
其中
。
证明:令
,利用引理2和条件2有
此处
为某个正常数,不同的地方
取值可不同。
因此有
。
由于
利用引理3和文献 [12] 知
。
综上可得
。
定理1的证明:
由于
, (3.1)
这表明0是集合
所构成的凸包的内点,
因此
存在为正。 (3.2)
观察到
, (3.3)
对上式右端对
求上确界时,满足
。
利用拉格朗日乘子法,可得
。 (3.4)
此处
,且满足
(3.5)
再利用引理3知:
,利用引理2得
。(3.6)
令
满足
,
利用(3.6)式及引理1知:
。 (3.7)
则有
。
令
利用(3.6),(3.7)式和引理4可得
。
借助Taylor展开,我们有
,对某正数
有
。
则有
。 (3.8)
再利用引理3知:
,
。 (3.9)
由条件得:
。 (3.10)
又由(3.6)和引理2得
其中
为某个正数,故有
。 (3.11)
综合(3.9)~(3.11)式便得
,
。 (3.12)
定理2的证明:
只需证明
。 (3.13)
观察到
,对上式右端对
求上确界时,
满足
。
借助拉格朗日乘子法得
, (3.14)
此处 ,且满足
,且满足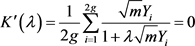 。
。
利用引理1证明得 。 (3.15)
。 (3.15)
有 。 (3.16)
。 (3.16)
 。 (3.17)
。 (3.17)
展开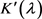 得
得 (3.18)
(3.18)
此处 。
。
利用引理4得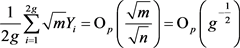 。 (3.19)
。 (3.19)
利用(3.18)及(3.19)式得 。 (3.20)
。 (3.20)
又由引理1,引理2,(3.17)及(3.20)式知 。记
。记 。
。
利用(3.17)和(3.18)式得: 。 (3.21)
。 (3.21)
又展开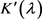 可得
可得
 。
。
记 ,有
,有 。 (3.22)
。 (3.22)
利用引理4和(3.18)式得
 。 (3.23)
。 (3.23)
又利用(3.21),(3.22)和(3.24)式得
 。 (3.24)
。 (3.24)
利用(3.23)式并利用Taylor展开式,则有

 (3.25)
(3.25)
此处 。
。
利用引理3及引理4,得 ,
, 。 (3.26)
。 (3.26)
利用(3.24)式得 。 (3.27)
。 (3.27)
利用(3.18)和(3.24)式得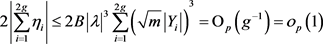 ,
,
从而可得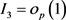 。 (3.28)
。 (3.28)
综上(3.25)~(3.28)式得 ,
,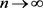 。 (3.29)
。 (3.29)
基金项目
本论文得到广东省自然科学基金项目资助(2016A030313812; 2018A030307070)。
文章引用
黄 娟. 正相协相依样本下分布函数的经验似然统计推断
Empirical Likelihood Statistic Inference for Distribution Function for PA Dependent Samples[J]. 理论数学, 2019, 09(01): 89-97. https://doi.org/10.12677/PM.2019.91012
参考文献
- 1. Joag-Dev, K. and Proschan, F. (1983) Negative Association of Random Variable with Application. The Annals of Statistics, 11, 286-295.
- 2. Owen, A.B. (1988) Empirical Likelihood Ratio Confidence Intervals for a Single Function. Biometrika, 75, 237-249.
https://doi.org/10.1093/biomet/75.2.237
- 3. Owen, A.B. (1990) Empirical Likelihood Confidence Regions. The Annals of Statistics, 18, 90 -120.
https://doi.org/10.1214/aos/1176347494
- 4. 张军舰, 王成名, 等. 相依样本情形下经验似然比置信区间[J]. 高校应用数学学报, 1999, 14(1): 63-72.
- 5. Kitamura, Y. (1997) Empirical Likelihood Methods with Weakly Dependent Process. The Annals of Statistics, 25, 2084-2102.
https://doi.org/10.1214/aos/1069362388
- 6. Lin, L. and Runchu, Z. (2001) Block Empirical Edulidean Likelihood for Weakly Dependent Process. Statistics & Probability Letters, 53, 143-152.
https://doi.org/10.1016/S0167-7152(01)00066-9
- 7. Birkel, T. (1988) Moment Bounds for Dependent Associated Sequences. The Annals of Probability, 16, 1184-1193.
https://doi.org/10.1214/aop/1176991684
- 8. Zhang, J.J. (2006) Empirical Likelihood for NA Series. Statistics & Probability Letters, 76, 153-160.
https://doi.org/10.1016/j.spl.2005.07.019
- 9. Chen, S.X. and Wong, C.M. (2009) Smoothed Block Empirical Likelihood for Quantiles of Weakly Dependent Processes. Statistica Sinica, No. 19, 71-81.
- 10. Zhang, J.J. (2007) Empirical Likelihood Ratio Confidence Interval for Positively Associated Series. Acta Mathematica Applicate Sinica-English Series, No. 23, 245-254.
- 11. Newman, C.M. (1984) Asymptotic Independence and Limit Theorems for Positive and Negative Dependent Random Variable. Inequalities in statistics and Probability, Hayward, 127-140.
- 12. 杨善朝. 随机变量部分和的矩不等式[J]. 中国科学, A辑, 2000, 30(3): 218-223.







 ,且满足
,且满足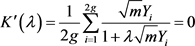 。
。 。 (3.15)
。 (3.15) 。 (3.16)
。 (3.16) 。 (3.17)
。 (3.17)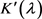 得
得 (3.18)
(3.18) 。
。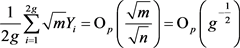 。 (3.19)
。 (3.19) 。 (3.20)
。 (3.20) 。记
。记 。
。 。 (3.21)
。 (3.21)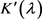 可得
可得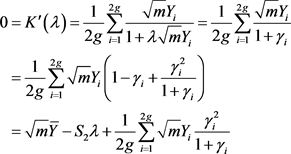 。
。 ,有
,有 。 (3.22)
。 (3.22) 。 (3.23)
。 (3.23) 。 (3.24)
。 (3.24)
 (3.25)
(3.25)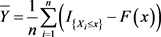 。
。 ,
,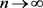 。 (3.26)
。 (3.26)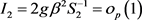 。 (3.27)
。 (3.27)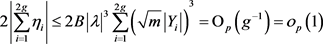 ,
,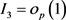 。 (3.28)
。 (3.28) ,
,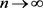 。 (3.29)
。 (3.29)