Pure Mathematics
Vol.
09
No.
08
(
2019
), Article ID:
32730
,
8
pages
10.12677/PM.2019.98122
The Efficient Finite Volume Element Methods for Semilinear Parabolic Equations
Zhiguang Xiong, Yi Wang, Juan Ma
School of Mathematics and Computational Science, Hunan University of Science and Technology, Xiangtan Hunan

Received: Sep. 30th, 2019; accepted: Oct. 22nd, 2019; published: Oct. 29th, 2019

ABSTRACT
In this paper, the fully discrete finite volume element schemes for a class of semi-linear parabolic equations are studied. Firstly, the initial value problem of the first-order nonlinear ordinary differential equations with time is obtained by interpolation coefficient finite volume element in space, and then the fully discrete scheme is obtained by backward difference method in time. Secondly, the stability and convergence of the fully discrete scheme are discussed. Finally, a numerical example is given to illustrate the efficiency of the proposed method.
Keywords:Semilinear Parabolic Equations, Interpolation Coefficient Finite Volume Element, Totally Discrete Scheme, Stability
半线性抛物问题高效有限体积元法
熊之光,王易,马娟
湖南科技大学,数学与计算科学学院,湖南 湘潭

收稿日期:2019年9月30日;录用日期:2019年10月22日;发布日期:2019年10月29日

摘 要
本文研究了一类半线性抛物方程的有限体积元全离散格式。首先在空间上以插值系数线性有限体积元进行半离散,得到关于时间的一阶非线性常微分方程组的初值问题,然后在时间上采用向后差分方法得到全离散格式。其次讨论了该全离散格式的稳定性和收敛性。最后给出了一个数值例子说明所研究方法的高效性。
关键词 :半线性抛物方程,插值系数有限体积元,全离散格式,稳定性

Copyright © 2019 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 前言
有限体积元方法(Finite Volume Method)是一种求解偏微分方程的数值方法,国内学者最早由李荣华教授提出 [1],在国外,该方面文章较早出现于二十世纪八十年代末 [2]。插值系数有限元方法的基本思想最早在1980年由Zlamal等提出 [3] [4],并用这种思想成功解决拟线性抛物问题,它的基本思路是在用有限元方法求解的过程中对非线性项直接插值处理,这样既简化了计算存储空间,又能保证所求数值解的超收敛性 [5]。插值系数有限元方法对于求解半线线性问题非常有效 [6] [7] [8]。类似地,将插值思想应用于微分方程的有限体积元法中,就得到插值系数有限体积元方法 [9] [10] [11] [12]。
本文将把插值系数有限体积元方法推广到半线性抛物问题中。考虑如下半线性抛物方程的初边值问题的有限体积元全离散格式
(1.1)
其中 为充分光滑函数,且 。本文将作如下安排:第2节构造出有限体积元的全离散格式,先在空间方向上进行半离散,再在时间方向上分别采用向前差分法、向后差分法得到两种全离散格式。第3节针对本文所给的问题得到的两种全离散格式,讨论其稳定性并给出证明。第4节给出两个数值例子以说明该方法的有效性。
2. 有限体积元格式
2.1. 空间有限体积元半离散
问题(1.1)的变分形式为,对每一个t,寻求 ,使得
(2.1)
其中 ,
(2.2)
对区间 作如下剖分:
设单元 ,每个单元的中点记为 ,步长 ,,
并假设剖分 是拟一致的,即存在常数 使得 ,另外设 , ,,那么所有的 构成 的对偶剖分 ,每个 也称为体积控制元.设基于剖分 的试探函数空间为 对每个t, 在节点 上的基函数为:
设基于对偶剖分 的函数空间 的为分片常数空间,对每个t, 在节点 上的基函数为:
对每个t,我们再定义插值算子 ,,和插值算子 ,。则问题(1.1)的插值系数线性有限体积元解 满足
(2.3)
这里 分别为
其中 。则式(2.3)可以等价的表示为
(2.4)
即
(2.5)
其中 。注意到 ,且 ,(2.5)得到如下计
算格式:
(2.11)
其中
如下向量记号:
相应的 系数矩阵记为 ,则式(2.11)用矩阵表示为:
(2.12)
另记
则方程(1.1)在空间上用线性有限体积元方法离散,得到如下的 关于t的一阶常微分方程组
(2.13)
2.2. 时间差分全离散
在式(2.13)中,由于 是严格对角占优矩阵,故 可逆,则式(2.13)可化为
(2.14)
将时间区域
分成N等分,节点为
,步长为
,将式(2.14)在节点 处离散化,对充分光滑的解
,利用向后差分可得
处离散化,对充分光滑的解
,利用向后差分可得
(2.17)
即得到单步隐式格式:
(2.18)
其中
,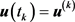 ,
。在式(2.18)中,令
,
。在式(2.18)中,令
(2.19)
则式(2.18)可化为
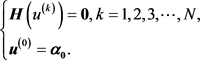 (2.20)
(2.20)
利用Newton迭代法可得
(2.21)
这里的
表示
的第l次迭代,
表示对矩阵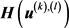 求导,
表示
求导,
表示 的逆矩阵,对式(2.19)求导可得
的逆矩阵,对式(2.19)求导可得
(2.22)
其中
利用(2.21)式,就可得到方程(1.1)的数值解。
3. 有限体积元全离散格式的稳定性与收敛性
本节讨论有限体积元全离散格式的稳定性,在这之前,先做一些准备工作。
定义3.1 设 的特征值为 ,称
为 的谱半径。
设 是方程组 的精确解, 是其迭代解,记误差向量 ,则有
即
其中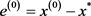 与k无关,所以
迭代收敛的充要条件为对于任意
,都有
与k无关,所以
迭代收敛的充要条件为对于任意
,都有
根据文献 [13],有如下两个引理:
引理3.1 设矩阵
,则 的充要条件是
。
的充要条件是
。
引理3.2 对于任意的初始向量 和右端向量f,解方程组 的迭代法 稳定的充要条件是 。
引理3.3 对于本文中的矩阵 ,若 ,则 。
证明 由于 ,则
其中
表示伴随矩阵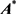 的元素,从而
的元素,从而
引理3.3得证。
为了方便起见,引入一些记号,令 为方程(1.1)的精确解, 为方程(1.1)的半离散解, 为方程(1.1)的全离散解,即有限体积元方法的数值解。
有了上面的准备,下面来讨论有限体积元方法的稳定性及其证明。
本小节中考虑线性有限体积元向后差分全离散格式,由式(1.19)得向后差分全离散迭代格式为
(3.5)
其中 .
定理3.2对方程(1.1)采用有限体积元向后差分全离散迭代格式(3.5)时,在任何剖分的情况下都是稳定的,即稳定性与时间剖分、空间剖分的密度无关。
证明 由于 是正定的,因此特征值 ,从而 的特征值 ,即 ,亦即 ,所以 ,即
(3.6)
由(3.5)可得 ,所以
其中
,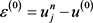 ,则由式(3.6)及引理3.2可得迭代格式(3.5)是稳定的,与h无关。定理3.2得证。
,则由式(3.6)及引理3.2可得迭代格式(3.5)是稳定的,与h无关。定理3.2得证。
4. 数值例子
为验证半线性抛物问题的有限体积元方法的有效性,本节给出下面例子。
例 求解如下半线性抛物问题
(4.1)
这里取 ,则其精确解为 。
分别采用线性有限体积元半离散,时间向后差分全离散格式进行数值计算。依次取均匀空间步长h和均匀时间步长
。表1给出了当
时,网格比为
的节点在N = 10,20,40,80的绝对误差值。其中u表示精确解,
至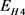 表示在N = 10,20,40,80时相应剖分下的绝对误差。表2给出了相应剖分下的绝对误差最大值和节点平均值误差,其中
表示在不同剖分下的节点绝对值误差最大值,
表示节点平均误差值。
表示在N = 10,20,40,80时相应剖分下的绝对误差。表2给出了相应剖分下的绝对误差最大值和节点平均值误差,其中
表示在不同剖分下的节点绝对值误差最大值,
表示节点平均误差值。
Table 1. Absolute errors of linear finite element with time backward difference for (4.1) under different partitions
表1. 问题(4.1)线性有限元时间向后差分在不同剖分下的绝对误差
Table 2. Problem (4.1) maximum absolute error and average error of linear finite element with time backward difference under different subdivisions
表2. 问题(4.1)线性有限元时间向后差分在不同剖分下的绝对误差最大值和平均误差值
从表1,表2可以看出用线性有限元时间向后差分全离散格式求解半线性抛物问题是可靠的。它的精度不仅与剖分密度有关,还与时间和空间的相对密度有关,也就是说,当剖分密度越大,时间和空间的相对密度越大,则利用该方法的精度越高。
基金项目
本文为国家自然科学基金项目(11571102)资助课题。
文章引用
熊之光,王 易,马 娟. 半线性抛物问题高效有限体积元法
The Efficient Finite Volume Element Methods for Semilinear Parabolic Equations[J]. 理论数学, 2019, 09(08): 961-968. https://doi.org/10.12677/PM.2019.98122
参考文献
- 1. 李荣华. 两点边值问题的广义差分法[J]. 吉林大学自然科学学报, 1982(1): 26-40.
- 2. Bank, R.E. and Rose, D.J. (1987) Some Error Estimates for the Box Method. SIAM Journal on Numerical Analysis, 24, 777-787. https://doi.org/10.1137/0724050
- 3. Zlamal, M. (1977) Finite Element Methods for Nonlinear Parablic Equations. RAIRO Model Anal Numer, 11, 93-107. https://doi.org/10.1051/m2an/1977110100931
- 4. Zlamal, M. (1980) A Finite Element Solution of the Nonlinear Heat Equation. RAIRD Model Anal Numer, 14, 203-216.
- 5. 熊之光. 插值系数有限元超收敛分析[M]. 南京: 东南大学出版社, 2015.
- 6. 熊之光, 陈传淼. 三角形二次插值系数有限元法解半线性椭圆问题的超收敛性[J]. 数学物理学报, 2006, 26A(2): 174-182.
- 7. Xiong, Z. and Chen, C.M. (2006) Superconvergence of Rectangular Finite Element with Interpolated Coefficients for Semilinear Elliptic Problem. Applied Mathematics and Computation, 181, 1577-1584. https://doi.org/10.1016/j.amc.2006.02.040
- 8. Xiong, Z. and Chen, C.M. (2007) Superconvergence of Continuous Finite Elements with Interpolated Coefficients for Initial Value Problems of Nonlinear Ordinary Differential Equation. Numerical Mathematics Theory Methods and Applications, 16, 37-44.
- 9. Xiong, Z.G. and Chen, Y.P. (2007) Finite Volume Element Method with Interpolated Coefficients for Two-Point Boundary Value Problem of Semilinear Differential Equations. Computer Methods in Applied Mechanics and Engineering, 196, 3798-3804. https://doi.org/10.1016/j.cma.2006.10.042
- 10. Xiong, Z.G. and Chen, Y.P. (2014) Triangular Finite Volume Element Method with Interpolated Coefficients for a Semilinear Elliptic Equation. Journal of Computational Mathematics, 32, 152-168. https://doi.org/10.4208/jcm.1310-FE3
- 11. Chatzipantelidis, P., Ginting, V. and Lazarov, R.D. (2005) A Finite Volume Element for a Non-Linear Elliptic Problem. Numerical Linear Algebra with Applications, 12, 515-546. https://doi.org/10.1002/nla.439
- 12. Xiong, Z.G. and Deng, K. (2017) A Quadratic Triangular Finite Volume Element Method for a Semilinear Elliptic Equation. Advances in Applied Mathematics, 9, 186-204. https://doi.org/10.4208/aamm.2014.m63
- 13. 韩旭里. 数值分析[M]. 北京: 高等教育出版社, 2011.
