Pure Mathematics
Vol.
09
No.
09
(
2019
), Article ID:
33214
,
6
pages
10.12677/PM.2019.99136
On the Weak Locality of a Field Algebra and Its Quotient Space
Xiaopei Chen, Xiandong Wang
School of Mathematics and Statistics, Qingdao University, Qingdao Shandong
Received: Nov. 3rd, 2019; accepted: Nov. 22nd, 2019; published: Nov. 29th, 2019

ABSTRACT
In this paper, we investigate the weak locality of a field algebra and give a concrete example which relates to weak locality and non-locality. The quotient space of a field algebra is obtained by its bilateral ideals. Finally, some theorems on the quotient space of a field algebra are explored.
Keywords:Field Algebra, Vertex Algebra, Weak Locality, Bilateral Ideals, Quotient Space
场代数弱局部性与商空间的研究
陈晓培,王宪栋
青岛大学数学与统计学院,山东 青岛
收稿日期:2019年11月3日;录用日期:2019年11月22日;发布日期:2019年11月29日

摘 要
本文对场代数的弱局部性进行了研究,给出了一个具体的例子,用于比较算子的弱局部性与非局部性。对场代数关于其双边理想做商得到商空间,并探究了场代数商空间的若干基本性质。
关键词 :场代数,顶点代数,弱局部性,双边理想,商空间

Copyright © 2019 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
场代数是顶点代数概念的“非局部性”推广。在顶点代数的定义中,局部性是一个基本的条件,把它换成较弱的结合性条件,将得到一个新的代数结构——场代数。由于场代数与顶点代数之间有着如此密切的联系,对场代数的研究将有助于更好的理解顶点代数及其相关领域。
在文献 [1] 中,作者系统讨论了态场对应、场代数的定义及初等性质,并且研究了场代数和顶点代数之间的关系,研究了态场对应的弱局部性和莱布尼兹共形代数上的张量代数等等。文献 [2] 研究了场代数的结合性,文献 [3] 和 [4] 分别引进了局部共形场代数和全场代数。本文将在上述文献给出的基本概念的基础上,探讨弱局部性与非局部性之间的关系,并给出具体实例加以说明。另外,本文对场代数的商空间也进行了描述,并讨论了一些基本性质。
本文假设所讨论的向量空间与各种代数结构都是指某个固定的域F上的,F可以是一般的域,必要时还可以假定它是复数域,从而保障线性变换特征值与特征向量的存在性。关于顶点代数的系统讨论,以及本文用到的一些术语与记号,参见文献 [5] [6] [7] [8] [9]。
设V是一个向量空间, ,若有线性映射:
及自同态 ,使得下列条件成立:
1) 真空性 ,,其中 是恒等变换;
2) 平移不变性 (称T是V上的平移算子);
则称三元组 是态场对应。
进一步,若态场对应 满足结合性公理:对 ,有
则称三元组 为场代数。
2. 预备知识
定义2.1 [1]:对 ,若有正整数N,使得 ,则称二元对 是N-弱局部的。若对充分大的N,总有 ,则称二元对 是弱局部的。
定义2.2 [5]:(局部性)对 ,若存在自然数 ,使得下列等式成立:
其中 ,则称 是相互局部的。
定义2.3 [1]:设V是场代数,I是V的子空间,且 。若有 ,,则称I是V的一个左理想。如果有 ,,则称I是V的一个右理想。若I既是左理想又是右理想,则I是V的一个双边理想。
3. 主要结果及证明过程
设V是域F上的向量空间,定义V上的算子向量空间
其加法和数乘运算都是自然定义的。称 是向量空间V上的场空间,其中的元素 为V上的场或算子。定义 上的双线性n-运算如下:
此时, 是F上的非结合代数,其中的算子也称为是下方截断的,见文献 [1]。
引理3.1:定义算子 ,使得 的系数 与 的任何系数可交换,则有 。此时,算子 是N-弱局部的。
进一步,若还有 ,则算子 是弱局部的。
证明:设 ,其中 。根据引理的条件,有下列等式:
即,等式 成立,算子 是N-弱局部的。
定理3.2:设算子 , 如上,且 是下方截断的。若有正整数 使得 ,,且算子 满足条件:对任意的正整数 ,存在非负整数n,使得系数 与 不可交换,则 不是局部的。
证明:对任意正整数 ,要证明 。根据前面的计算式,只要证明
选取 ,上述不等式化简为 。再根据定理条件: 与 不可交换,前面的不等式确实成立,从而算子 不是局部的。
注记:上述定理中的 不具有下方截断性。若要求 满足下方截断性,可选取正整数 ,使得 ,且 。此时,对任意的正整数 及整数k,满足: ,使得 ,且 ,这里 。取 ,使它与 不可交换。再令 ,则有下列式子:
从而有
因此,算子 不是局部的。
下面我们以二阶矩阵为例,给出一个具体的例子。
例3.3:1) 构造算子 :当 时, 为任意矩阵。当 时,令 。当 ,令 。当 ,令 。2) 构造算子 :当 时, 为任意矩阵。当 时, , 或者 。当 时, 。此时, 。因此, 是 -弱局部的,但是它们不是局部的。
讨论算子的弱局部性是为了构造场代数,而局部性的研究是顶点代数要面临的问题。下面的例子给出了一些说明,其详细讨论见文献 [1] 和文献 [8]。
例3.4:设子空间W是向量空间 的一个弱局部子空间,它包含恒等变换 ,且对n运算封闭,则 是一个态场对应。这里线性映射 定义如下:
其中 定义如上。若 满足结合性公理,则它是场代数。若还满足弱局部性,则它是强场代数。
引理3.5:设 是场代数,I是V的T不变的双边真理想,则 也是一个场代数。相应的线性映射可以如下给出:
证明:1) 合理性:商空间 中的n运算定义为: 。若 ,,则 ,I是V的双边理想,必有 。
于是, ,运算的定义是合理的。
2) 真空性: ,,其中 是恒等变换。
3) 平移不变性: ,T是 上的平移算子。
4) 因为 是场代数,对所有的 ,有下列结合性等式:
将上式变形,得到下列等式:
对商空间 中的任意元素 ,必有
故 也是一个场代数。
可以按照通常的方式定义场代数的同态,并且同态的核是理想,同态的像是场代数。
引理3.6:场代数的同态基本定理:设 是场代数 之间的同态,I是V的一个理想,并且 ,则有唯一的场代数同态 ,使得 。这里 是典范同态,而 。
特别,若 ,则 是单射,此时 是同构。
证明:

1) 令 。映射 定义合理:若 ,即 ,,有
。,。
2) 是同态: 。首先,它是向量空间的线性映。另外,它保持n运算:
3) 由 的定义直接看出: 。
4) 唯一性:若还有另外一个同态 ,使得 。则 。即 。由此可知, 。
5) 是双射:由定义直接看出。因此, 是场代数的同构映射。
引理3.7:设 是场代数,I是V的真理想,则商代数 的理想构成的集合B与V包含I的理想构成的集合A之间有一一对应。特别地, 的理想形如 ,这里L是V的包含I的理想。
证明:考虑典范态场对应同态 ,由此定义集合之间的映射
1)
是单射:设理想
,且
。,必有 。故存在
。故存在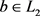 ,使得
,使得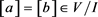 。于是
。于是 ,从而
,从而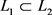 ,同理可得
,同理可得 ,则
,则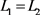 。
。
2) 是满射:设
是满射:设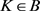 ,令
,令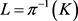 ,现证
,现证 。
。 ,
,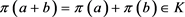 。从而
。从而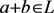 。
。 ,则
,则 ,同理可证
,同理可证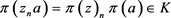 。因此,L是V的理想。另外,L是V的包含I的理想,即
。因此,L是V的理想。另外,L是V的包含I的理想,即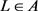 。最后由于典范映射
。最后由于典范映射 是满射,必有
是满射,必有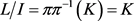 ,即
,即 是满射。
是满射。
因此, 是双射,引理结论成立。
是双射,引理结论成立。
引理3.8:设 是场代数,其中I,J为场代数
是场代数,其中I,J为场代数 的两个双边真理想,且有理想的包含关系:
的两个双边真理想,且有理想的包含关系: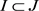 ,则有场代数之间的同构映射:
,则有场代数之间的同构映射: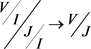 。
。
证明:由双边理想的定义可以验证 是
是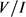 的双边理想,利用同态基本定理可以验证引理的结论成立。
的双边理想,利用同态基本定理可以验证引理的结论成立。
文章引用
陈晓培,王宪栋. 场代数弱局部性与商空间的研究
On the Weak Locality of a Field Algebra and Its Quotient Space[J]. 理论数学, 2019, 09(09): 1108-1113. https://doi.org/10.12677/PM.2019.99136
参考文献
- 1. Bakalov, B. and Kac, V.G. (2002) Field Algebras. International Mathematics Research Notices, 13, 123-159. https://doi.org/10.1155/S1073792803204232
- 2. Kim, N. (2011) Associativity of Field Algebras. Annales Henri Poincare, 12, 1145-1168. https://doi.org/10.1007/s00023-011-0092-5
- 3. Juriev, D. (1991) Local Conformal Field Algebras. Communications in Mathematical Physics, 138, 569-581. https://doi.org/10.1007/BF02102042
- 4. Huang, Y.Z. and Kong, L. (2007) Full Field Algebras. Communications in Mathematical Physics, 272, 345-396. https://doi.org/10.1007/s00220-007-0224-4
- 5. Gebert, R.W. (1993) Introduction to Vertex Algebras, Borcherds Algebras and the Monster Lie Algebra. International Journal of Modern Physics A, 8, 5441-5503. https://doi.org/10.1142/S0217751X93002162
- 6. Borcherds, R.E. (1986) Vertex Algebras, Kac-Moody Algebras and the Monster. Proceedings of the National Academy of Sciences of the United States of America, 83, 3068-3071. https://doi.org/10.1073/pnas.83.10.3068
- 7. Borcherds, R.E. (1998) Vertex Algebras. Mathematics, 160, 35-77. https://doi.org/10.1007/978-1-4612-0705-4_2
- 8. Lepowsky, J. and Li, H.S. (2004) Introduction to Vertex Operator Algebras and Their Representations. Progress in Mathematics, Volume 227. Birkhauser, Boston. https://doi.org/10.1007/978-0-8176-8186-9
- 9. Atiyah, M.F. and Macdonald, I.G. (1969) Introduction to Commutative Algebra. Addison-Wesley Publishing Company, Inc., Boston.