Pure Mathematics
Vol.
10
No.
04
(
2020
), Article ID:
35183
,
6
pages
10.12677/PM.2020.104043
A Survey on the Results of Ramanujan Expansion
Tianfang Qi
Department of Mathematics, South China University of Technology, Guangzhou Guangdong
Received: Mar. 24th, 2020; accepted: Apr. 13th, 2020; published: Apr. 22nd, 2020

ABSTRACT
The Ramanujan sum is an important tool in modern number theory, and it recently has been found many applications in information sciences. This is mainly because the results obtained by the Hungarian mathematician Wintner and the French mathematician Delange in 1976: the arithmetic functions in one variable defined on can be expanded through the Ramanujan sums, which is similar with the Fourier expansions in the classical analysis. Subsequently, Ushiroya and Tóth generalized this result to the multi-variable cases. Based on the works of Zheng, recently we also proved that a large class of arithmetic functions in multi-variables defined on , the polynomial ring over a finite field, can also be expanded through the Ramanujan sums introduced by Carlitz and Cohen. This note will give a survey on the results of Ramanujan expansions mentioned above. All the proofs of the results in this note can be found in the references of this article.
Keywords:Arithmetic Function, Ramanujan Sum, Zeta Function, Polynomial Ring over a Finite Field

有关Ramanujan展开的结果的综述
齐田芳
华南理工大学数学学院,广东 广州
收稿日期:2020年3月24日;录用日期:2020年4月13日;发布日期:2020年4月22日

摘 要
Ramanujan和是现代数论中的一个重要工具,近年来也在信息科学中得到较多应用。这主要是基于匈牙利数论学家Wintner和1976年法国数论学家Delange的结果:整数环上的单变量算术函数都可以通过Ramanujan和加以展开。这类似于经典分析中的Fourier展开。随后这一结论被Ushiroya和匈牙利数论学家Tóth推广到了多变量情形。基于郑志勇教授的工作,最近我们证明了定义在有限域上一元多项式环 上的一大类算术函数(包括单变量和多变量情形)也可以通过Carlitz和Cohen定义的Ramanujan和加以展开。本文将对上面所得到的有关Ramanujan展开的结果进行综述。本文所有结果的证明都能在文末的参考文献中找到。
关键词 :算术函数,Ramanujan和,Zeta函数,有限域上的一元多项式环

Copyright © 2020 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
一百年前,印度著名数学家Ramanujan首次定义了如下经典的Ramanujan和:
, (1)
其中 为正整数集, 是k和q的最大公因子。
式(1)满足许多好的性质(见文献 [1],8.3节),并且有以下等式成立:
, (2)
其中 是经典的Möbius函数。
令d和n都是整数。若 且 ,则称d是n的一个酉因子,并记为 。美国数论学家
E. Cohen [2] 于1959年给出了酉Ramanujan和的定义(也可见文献 [3],3.2节)
, (3)
其中 。
2. 结果
本部分我们将综述至今为止所得到的有关多元算术函数的Ramanujan展开的结果,这些结果涉及整数环 以及有限域上的一元多项式环 。
本部分所有结果的证明都能在文末参考文献中找到。
1976年,法国数论学家Delange [4] 在Wintner [5] 结果的基础上证明了定义在 上单变量算术函数都可以通过Ramanujan和(1)加以展开。这类似于经典数学分析中周期函数的Fourier展开式。他的结果如下。
定理2.1 (见Delange [4]) 令 是任一算术函数。如果
.
那么对任意的 ,我们有下面绝对收敛的Ramanujan展开式
,
其中系数 从下式中得到
.
另外,Delange [4] 还得到定理2.1对于乘性函数的应用。需要指出的是,在Delange [4] 之前,Cohen [6] 也曾对某些特殊的单变量乘性函数类得到了推出绝对收敛的Ramanujan展开式的方法。
Ushiroya [7] 于2016年将定理2.1推广到两个变量的情形,同时得到了定义在 上某些特殊函数的经典Ramanujan展开式的具体表达。
在Delange [4] 和Ushiroya [7] 所得结果以及酉Ramanujan和(3)定义的基础上,2018年,匈牙利数论学家Tóth [3] 考虑将定理2.1推广到多元情形,证明了定义在 上的多元算术函数都可以通过Ramanujan和(1)与酉Ramanujan和(3)加以展开。
定理2.2 (Tóth [3],定理2)令 是任一算术函数 。如果
. (4)
那么对任意的 ,我们有
(5)
和
, (6)
其中
(7)
并且级数(5)和(6)是绝对收敛的。
注2.1. 在定理2.2中令 和 可以分别得到Delange [4],Ushiroya [7] 的结论。
记 的最大公因子,g是从 到 的算术函数。在定理2.2中令 ,Tóth [3] 进一步得到下面的结果。
定理2.3 (Tóth [3],定理3) 令 是一个算术函数且 。如果
. (8)
那么对任意的 ,我们有下面绝对收敛的级数
(9)
和
, (10)
其中
(11)
且 。
注2.2. 注意到乘性函数可以由其在素幂处的值完全确定,由此结果还可进一步得到 上某些特殊的多元乘性函数关于经典Ramanujan和以及酉Ramanujan和展开式的具体表达(详见 [3],推论1和推论2),更进一步地,它们与经典的Riemann zeta函数 有关。
设 是有限域上一元多项式环 中首一多项式的全体。类比经典的Ramanujan和(1),美国著名数论学家L. Carlitz [8] 首次引入 上的多项式Ramanujan和的定义,然后由E. Cohen在文 [9] 中加以推广。我国数论学家郑志勇教授在最近的文献 [10] 中系统地研究了多项式Ramanujan和的性质。
下面我们简要介绍一下多项式Ramanujan和的定义。假设 是 中一固定的m次多项式。若
,
则有 上模H的加性函数
, 对任意的 .
对任意的 ,我们有
, 如果 ,
特别地,如果 ,那么 。
对任意给定的 ,令 ,我们可以看出, 也是一个模H的加性函数。
再令 ,其中 , 是从 到 的迹函数,则 是 上模H的加性特征。
定义2.1 (见Carlitz [8],(4.1)式或郑志勇 [10],(1.10)式) 令 是 中全体首一多项式构成的集合。对于 ,模H的多项式Ramanujan和 定义为
, (12)
其中 是D和H的首一的最大公因子。
注2.3. 郑志勇教授在文 [10] 中研究了许多有关多项式Ramanujan和(12)的性质。
类比酉Ramanujan和的定义(3),我们下面在 上定义酉多项式Ramanujan和。
定义2.2 (见齐田芳和胡甦 [11],定义1.4)对于 ,我们定义 上的酉多项式Ramanujan和 为:
, (13)
其中 ,即 是多项式集合 中次数最高的元。
接下来,类比Tóth在文 [3] 中关于数域的工作,我们得到了 上的多元算术函数(定义见文献 [11],定义1.5)都可以通过多项式Ramanujan和以及酉多项式Ramanujan和加以展开。我们在文 [11] 中已经得到的结果如下(所涉及到的基本符号见文献 [11] [12])。
定理2.4 (见齐田芳和胡甦 [11],定理1.7)令 是任一算术函数, 。如果
. (14)
那么对任意的 ,我们有
, (15)
和
, (16)
其中
(17)
并且式(15)和(16)都是绝对收敛的。
设g是从 到 的算术函数。在定理2.4中令 ,这里 是 的最大公因子,我们在文 [11] 中又得到了下面的结果。
定理2.5 (见齐田芳和胡甦 [11],定理1.8)设 是任一算术函数, 。若
. (18)
则对任意的 ,我们有下面绝对收敛的级数
, (19)
和
, (20)
其中
(21)
且 ,即Q是 的最小公倍式 。
注2.4. 注意到 上的乘性函数都可以由它们在首一不可约多项式处的值完全确定,我们在文 [11] 中将定理2.5应用到乘性函数上,进一步得到了 上的某些特殊多元乘性函数关于多项式Ramanujan和(12)以及酉多项式Ramanujan和(13)展开式的具体表达(详见 [11],推论3.4和推论3.5),并且它们与 上的Zeta函数
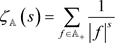
有关(见文献 [11])。
文章引用
齐田芳. 有关Ramanujan展开的结果的综述
A Survey on the Results of Ramanujan Expansion[J]. 理论数学, 2020, 10(04): 339-344. https://doi.org/10.12677/PM.2020.104043
参考文献
- 1. Apostol, T.M. (1976) Introduction to Analytic Number Theory. Undergraduate Texts in Mathematics. Springer-Verlag, New York/Heidelberg. https://doi.org/10.1007/978-1-4757-5579-4
- 2. Cohen, E. (1960) Arithmetic Functions Associated with the Unitary Divisors of an Integer. Mathematische Zeitschrift, 74, 66-80. https://doi.org/10.1007/BF01180473
- 3. Tóth, L. (2018) Ramanujan Expansions of Arithmetic Functions of Several Variables. Ramanujan Journal, 47, 589-603. https://doi.org/10.1007/s11139-017-9944-z
- 4. Delange, H. (1976) On Ramanujan Expansions of Certain Arithmetic Functions. Acta Arithmetica, 31, 259-270. https://doi.org/10.4064/aa-31-3-259-270
- 5. Wintner, A. (2017) Eratosthenian Averages. Waverly Press, Balti-more.
- 6. Cohen, E. (1961) Fourier Expansions of Arithmetical Functions. American Mathematical Society, 67, 145-147. https://doi.org/10.1090/S0002-9904-1961-10542-9
- 7. Ushiroya, N. (2016) Ramanujan-Fourier Series of Certain Arithmetic Functions of Two Variables. Hardy-Ramanujan Journal, 39, 1-20.
- 8. Carlitz, L. (1947) The Singular for Sums of Squares of Polynomials. Duke Mathematical Journal, 14, 1105-1120. https://doi.org/10.1215/S0012-7094-47-01484-1
- 9. Cohen, E. (1949) An Extension of Ramanujan’s Sum. Duke Mathematical Journal, 16, 85-90. https://doi.org/10.1215/S0012-7094-49-01607-5
- 10. Zheng, Z. (2018) On the Polynomial Ramanujan Sums over Finite Fields. Ramanujan Journal, 46, 863-898. https://doi.org/10.1007/s11139-017-9941-2
- 11. Qi, T. and Hu. S. (2018) Ramanujan Expansions of Arithmetic Functions of Several Variables over Fq[T].arXiv:1811.01654 [math.NT]
- 12. Rosen, M. (2002) Number Theory in Function Fields. GTM, Vol. 210. Springer, New York. https://doi.org/10.1007/978-1-4757-6046-0