Computer Science and Application
Vol.
09
No.
05
(
2019
), Article ID:
30413
,
5
pages
10.12677/CSA.2019.95104
Fault Detection of Power Converter under Uncertain Noise Disturbances
Zixing Liu, Ziyun Wang*, Yan Wang, Zhicheng Ji
Engineering Research Center of Internet of Things Technology Applications Ministry of Education, Jiangnan University, Wuxi Jiangsu

Received: May 6th, 2019; accepted: May 20th, 2019; published: May 27th, 2019

ABSTRACT
A fault detection method based on set membership estimation is proposed for power converter systems with unknown but bounded uncertain noise disturbances. Taking Buck converter as an example, the current and voltage values obtained by simulation are taken as input of set membership estimation. The feasible set of all parameters is surrounded by ellipsoid and it can be concluded that the Buck converter is faulty when the approximate feasible set is empty set.
Keywords:Set Membership Estimation, Power Converter, Fault Detection
不确定噪声扰动下的电力变换器故障检测
刘子幸,王子赟*,王艳,纪志成
江南大学物联网技术与应用教育部工程中心,江苏 无锡

收稿日期:2019年5月6日;录用日期:2019年5月20日;发布日期:2019年5月27日

摘 要
针对未知但有界的不确定噪声扰动下的电力变换器系统,提出了一种基于集员估计的故障检测方法。以Buck变换器为例,将其仿真所得电流电压数值作为集员估计的输入,通过椭球包围所有参数的可行集,当近似可行集为空集时可以判定Buck变换器存在故障。
关键词 :集员估计,电力变换器,故障检测

Copyright © 2019 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
电力变换器广泛应用于能源、航天、农业等领域中 [1] [2] [3] ,随着应用范围的不断拓展,对电力变换器的稳定性和可靠性的要求越来越高,一旦电力变换器发生故障而未被及时检测出来,则会进一步引起系统中其他模块的故障,导致整个系统故障严重甚至瘫痪,因此,为保证电力系统的安全,提高相关领域的经济效益,对电力变换器进行快速准确的故障诊断有着重要意义。
现有的电力变换器的故障诊断方法可分为基于解析模型的故障诊断方法、基于知识的故障诊断方法和基于信号处理的故障诊断方法三类 [4] 。其中基于解析模型的故障诊断方法因其故障诊断中良好的实时性能,近些年来取得了快速的发展。然而在实际情况中,系统干扰噪声等不定因素太多,常常难以得到实时、精确的数学模型,从而限制了基于解析模型的故障诊断方法的使用效果和应用范围。
本文主要针对上述基于解析模型的故障诊断方法中存在的不足,提出一种基于集员估计思想的故障检测方法。对于不确定噪声扰动下的Buck变换器系统,根据Simulink模块中所建立的仿真模型获取工作过程中的电感电流和输出电压值,将其作为集员估计算法的输入,从而得到包含其参数可行集的椭球集合,根据椭球集合的空集情况可判断出系统的故障状况。
2. 问题描述
Buck变换器电力变换器基本拓扑结构的一种,是一种用于降压变换的变换器。基于Buck变换器的基本拓扑结构,根据各器件的工作原理特性,将Buck变换器进行一定的等效简化,具体的等效简化步骤为:将电感视为理想器件;将开关管MOSFET视为理想开关S1,即只包含导通和断开两个状态;将二极管D视为理想开关S2,也只包含导通和断开两个状态;将电解电容器等效为串联电容C和等效串联电阻RC串联。等效简化后得到的Buck变换器等效原理图如图1所示。其中图中 表示流经电感的电流, 表示输出电压。

Figure 1. The equivalent schematic diagram of the Buck converter
图1. Buck变换器等效原理图
在MATLAB仿真软件中进行本实验的模型的搭建和算法的仿真。MATLAB仿真软件包含MATLAB和Simulink两部分,其中Simulink中包含了多种仿真软件包可方便对系统进行建模和仿真,MATLAB中也含有多个工具箱,为算法的仿真提供了便利。
基于Buck变换器等效原理图,可在MATLAB软件的Simulink模块中建立Buck变换器仿真模型,如图2所示。

Figure 2. The Simulink model of the Buck converter
图2. Buck变换器仿真模型
根据搭建的仿真模型,设置相应的仿真参数,可得到相对应的电感电流和输出电压的波形和数值。将仿真所得的电感电流和输出电压的波形和数值导入到MATLAB的Workspace中保存,作为基于集员估计的Buck变换器故障检测的模型数据。
3. 集员估计方法
集员估计是一种对含有未知但有界噪声的系统进行状态或参数估计的方法,目的是找到包含系统数学模型、量测数据和噪声边界的集合来描述系统的状态或参数,一般称之为状态或参数的可行集。通过输入数据的增加,可行集范围可不断缩小,以更进一步地确定系统的状态或参数。可行集的中心可以作为系统状态或参数的真实值的估计,但一般情况下可行集难以精确描述和求解,因而通常用包含可行集的近似可行集来对其进行描述。根据描述参数的近似可行集的形状不同,可将集员估计分为椭球算法、多面体算法、多胞形算法等 [5] 。
相比于一些传统的估计算法,集员估计方法有着显著优点,仅需要基于系统噪声有界的情况下就可以对有着随机噪声的系统进行处理,有着更好的实用性、普适性和鲁棒性。基于所述优点,集员估计方法运用广泛,可用于参数估计、故障诊断、定位导航等领域 [6] [7] [8] 。基于集员估计的故障检测方法是一种基于解析模型的鲁棒故障检测方法,是通过检测近似可行集是否为空集来对系统状态进行判断,如果检测出可行集为空集,则可判定系统发生故障。
4. 基于集员估计的Buck变换器故障检测
针对有着不确定噪声扰动下的Buck变换器系统,本文运用集员估计的方法对其进行故障检测。
首先依据Buck的等效原理图,建立起Buck变换器在CCM (Continuous Conduction Mode)模式下的混杂系统模型,并经过离散化处理后可得到相应的混杂系统离散模型表达式:
(1)
其中T为采样周期值。根据混杂系统离散模型表达式确定出k时刻Buck变换器系统的参数向量 、 ,观测矩阵 以及系统输出 、 ,从而可进一步得到相应的系统方程:
(2)
(3)
其中 、 分别代表了电感电流和输出电压的数值, 和 表示的是系统存在的不确定噪声向量,且都存在限定的噪声边界 和 。
以参数向量 的检测过程为例,参数向量 可参照进行。
基于系统方程(2),根据集员估计算法可得到其参数可行集
,之后根据前k组数据对应的参数可行集确定出k时刻包含所有可能参数的凸多面体集合 。然而凸多面体集合难以精确描述,因此为更好地进行描述,用尽可能紧地包含着凸多面体集合
的椭球集合
来描述参数向量
,得到的椭球集合
如下式所示:
。然而凸多面体集合难以精确描述,因此为更好地进行描述,用尽可能紧地包含着凸多面体集合
的椭球集合
来描述参数向量
,得到的椭球集合
如下式所示:
(4)
其中
表示椭球集合
的中心,
为表示椭球集合形状和大小的轴信息矩阵。根据上述式子,按集员估计递推公式可递推得到k时刻的椭球集合的相关信息,通过椭球中心和轴信息矩阵确定出k时刻对应参数向量
的椭球集合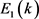 。
。
同理,可通过递推确定出k时刻对应参数向量 的椭球集合 。
当Buck变换器系统不存在故障时,则表示参数向量 和参数向量 对应的椭球集合都能够准确包围住相应的真值 和 ,也即表现出 , , 和 , , 的情况。而当Buck变换器系统发生故障时,则可能有 或 的情况发生。对于参数向量 ,此时的 , , 可能为空集。因此,在Buck变换器的故障检测中,可依据 和 的情况来确定其故障情况。具体判断如下:
1) 若
且
,则故障信号 ,表现出Buck变换器已发生故障;
,表现出Buck变换器已发生故障;
2) 若 且 ,则故障信号 ,表现出Buck变换器系统错误;
3) 若 且 ,则故障信号 ,表现出Buck变换器已发生故障;
4) 若 且 ,则故障信号 ,表现出Buck变换器未发生故障。
具体的 的判定可按照如下步骤进行:
定义 和 ,当 和 满足如下式子时,则可判定上述式子成立。
(5)
依据上述算法,能够准确确定出Buck变换器在工作过程中的工作状况,及时得到故障检测结果,对保证电力变换器的安全有效的运行提供了保障,促进了系统工作效率和经济效益的提升。
5. 结论
本文针对不确定噪声扰动下的电力变换器系统故障检测问题,提出了一种基于集员估计的故障检测方法。通过获得变换器系统的测量值和相应的噪声边界,可以通过集员估计方法得到系统的参数近似可行集,若过程中某一时刻有故障发生,则得到的近似可行集为空集,从而实现Buck变换器系统的故障检测。
基于集员估计的故障检测方法相比于一般的故障检测方法,能够对不确定但有界的噪声下的系统进行故障检测,有着良好的实用性和普适性,因此本文提出的基于集员估计的电力变换器故障检测方法具有广阔的研究和应用前景。而然作为一种故障检测方法,基于集员估计的方法在判断Buck变换器的具体故障位置中还存在一定的不足。为方便对Buck变换器的故障进行精确的研究,对所提的集员估计算法进行完善,能够实现准确的Buck变换器故障诊断是下一步的研究方向。
文章引用
刘子幸,王子赟,王 艳,纪志成. 不确定噪声扰动下的电力变换器故障检测
Fault Detection of Power Converter under Uncertain Noise Disturbances[J]. 计算机科学与应用, 2019, 09(05): 921-925. https://doi.org/10.12677/CSA.2019.95104
参考文献
- 1. 孟准, 王议锋, 杨良. 一种适用于小功率可再生能源的单相高频双Buck全桥并网逆变器[J]. 电工技术学报, 2017, 32(8): 220-228.
- 2. Buticchi, G., Barater, D., Costa, L.F., et al. (2018) A pv-Inspired Low-Common-Mode Du-al-Active-Bridge Converter for Aerospace Applications. IEEE Transactions on Power Electronics, 33, 10467-10477. https://doi.org/10.1109/TPEL.2018.2801845
- 3. Mishra, A.K. and Singh, B. (2017) Solar Photovoltaic Array Dependent Dual Output Converter Based Water Pumping Using Switched Reluctance Motor Drive. IEEE Transactions on Industry Applications, 53, 5615-5623. https://doi.org/10.1109/TIA.2017.2732341
- 4. 于生宝, 何建龙, 王睿家, 等. 基于小波包分析和概率神经网络的电磁法三电平变换器故障诊断方法[J]. 电工技术学报, 2016, 31(17): 102-112.
- 5. 刘玉双, 赵剡, 吴发林. 基于外定界椭球集员估计的纯方位目标跟踪[J]. 北京航空航天大学学报, 2017, 43(3): 497-505.
- 6. 沈强, 刘洁瑜, 赵乾, 王琪. 非线性系统中心差分集员估计方法[EB/OL]. 控制理论与应用, 1-11. http://kns.cnki.net/kcms/detail/44.1240.TP.20190408.1008.014.html, 2019-05-08.
- 7. 王子赟, 徐桂香, 刘子幸, 王艳, 纪志成. 基于正多胞体线性规划的滤波故障诊断方法[EB/OL]. 控制与决策, 1-9.
- 8. 周波, 钱堃, 马旭东, 戴先中. 基于集员估计的室内移动机器人多传感器融合定位[J]. 控制理论与应用, 2017, 34(4): 541-550.
*通讯作者。