Journal of Water Resources Research
Vol.04 No.02(2015), Article ID:15175,7
pages
10.12677/JWRR.2015.42024
The Application of the TOPSIS-Fuzzy Comprehensive Evaluation Method Used in the Method of Optimizing the Hydrologic Frequency Parameter Estimation
Guanjun Lei, Wenchuan Wang*, Kuan Liu, Lin Qiu
College of Water Conservancy, North China University of Water Resources and Electric Power, Zhengzhou Henan
Email: *wangwen1621@163.com
Received: Apr. 10th, 2015; accepted: Apr. 28th, 2015; published: May 5th, 2015
Copyright © 2015 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
Hydrological frequency parameter is estimated by method of moment, weight function method, numerical integral single (or double) weight function method, probability weighted moment method and so on. These methods all have their own theoretical basis and have been used to calculate the parameters of distribution as initial values. The graphical method can be used to directly with the optimum line to judge the merits of parameters with no quantitative evaluation criteria. The TOPSIS method combined with fuzzy comprehensive evaluation method is compared with TOPSIS-cosine method to be found that the method in this article has good performance evaluation. The results of this study show that the evaluation results conform to the optimal line method with four different evaluation criteria and the weighted method for quantitative analysis. The proposed method can be used in other multi-objective evaluation method with the strict evaluation theory.
Keywords:Hydrological Frequency Analysis, Parameter Estimation, TOPSIS Method, Fuzzy Comprehensive Evaluation

TOPSIS-模糊综合评判法在优选水文频率参数估计方法中的应用
雷冠军,王文川*,刘宽,邱林
华北水利水电大学水利学院,河南 郑州
Email: *wangwen1621@163.com
收稿日期:2015年4月10日;录用日期:2015年4月28日;发布日期:2015年5月5日

摘 要
矩法、权函数法、数值积分单权函数法、数值积分双权函数法以及概率权重矩法等方法是水文频率参数初值估计的常用方法,可直接通过图解法主观判断计算出的参数值的优劣,却没有定量的评价准则。为了寻求良好的评判方法,将TOPSIS方法与模糊综合评判方法相结合,并与传统的TOPSIS-余弦法相比较发现,TOPSIS-模糊综合评判法具有较良好的评价性能。采用四种不同的评价准则,运用加权法对传统的参数估计结果进行定量分析,评价结果与适线法的直观效果相符合,该方法具有较严密的理论评价基础和合理的评价结果,可用于其他多目标评价方法中。
关键词 :水文频率分析,参数估计,TOPSIS方法,模糊综合评判

1. 引言
在水利工程建设中,需要根据历史洪水资料来通过频率适线展延来确定设计水文值。洪水频率参数估计方法为适线法。而优化适线法在工程实践中采用数值解法求出参数的初值后加以人工适线,调整参数值不断适线以确定最优的参数值。计算参数初值的方法发展较快,比较常用的有:矩法[1] 、权函数法[2] 、数值积分权函数法[3] 、概率权重矩法[4] 以及数值积分双权函数法[5] 等。在适线比较时发现,不同的方法的精确度不同,这只是从人的上主观上去发现,但是没有一个科学合理的标准来说明参数确定的优劣。而适线法的优劣评判准则[6] 有:横、纵向离差平方和,横、纵向离差绝对值和,本文尝试从这四个评价指标出发,采用TOPSIS-模糊综合评判法对参数的确定结果进行评判,为参数的确定的优劣提供一个合理的标准。
2. TOPSIS综合评价方法
综合评价是指对一个复杂系统的多个指标通过对照某些标准来判断观测结果,并赋予这种结果以一定的意义和价值过程。综合评价分为:定性评价和定量评价。TOPSIS法(Technique for order preference by similarity to ideal solution)是有限方案多目标决策分析的一种常用方法,可用于效益评价、卫生决策和卫生事业管理等多个领域。Hwang和Yoon [7] 首次提出TOPSIS法,制定了靠近正理想解和远离负理想解两个基准来评价各个方案的依据。本法对资料无特殊要求,使用灵活简便,应用广泛。郭靖、郭生练[8] 将TOPSIS法与遗传算法相结合对四个目标函数进行综合评判,并与距离函数法相比较结果较好,定权过程中采用均方差法。钱吴永[9] 通过灰色关联度来确定指标的权重,与TOPSIS法相结合,建立了加权TOPSIS模型。本研究将在医学领域应用较广的TOPSIS法与模糊综合评判相结合,采用TOPSIS法计算权重,有效地对四个评价准则进行加权计算,评价结果更加合理有效。应用TOPSIS综合评价,能够有效提高管理决策的科学性,推动医学科学的发展,促进人们思想观念的变化,同时能够促进理论研究水平的提高。
综合评价的一般步骤是:(1) 筛选制定指标评价体系;(2) 确定各评价指标的权重;(3) 确定各指标的评价等级及界限;(4) 选定适合的综合评价方法,建立评价数学模型;(5) 对评价结果进行综合分析和判断,作出评价等级(结果)。
3. TOPSIS-余弦法
此方法的基本思想是基于归一化后的原始数据矩阵,采用余弦法找出有限方案中的最优方案和最劣方案(分别用最优向量和最劣向量表示),然后分别计算各评价对象与最优方案和最劣方案间的距离,获得各评价对象与最优方案的相对接近程度,以此作为评价优劣的依据。计算步骤:
设有n个评价对象,m个评价指标,原有数据形式为表1。
(1) 指标数据的处理
指标属性趋同化处可将低优指标和中性指标全转化为高优指标 ,方法是:
,方法是:
 (1)
(1)
并适当调整(扩大或缩小一定比例)转换数据。
(2) 趋同化数据的无量纲化
 (2)
(2)
(3) 确定最优方案和最劣方案
最优方案每列中的最大值组成: ;
;
最劣方案每列中的最小值组成: 。
。
(4) 计算每一个评价对象与 、
、 的距离
的距离 、
、 :
:
 (3)
(3)
(5) 计算各评价对象与最优方案的接近程度 :
:
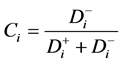 (4)
(4)
 ,
, ,表明评价越优。
,表明评价越优。
(6) 按 大小排序,定出评价结果。
大小排序,定出评价结果。
4. TOPSIS-模糊综合评价法
该方法的基本思想是利用TOPSIS法来确定指标权重,与模糊综合评判方法相结合,构建了基于TOPSIS定权的模糊综合评判法模型,并给出了计算步骤。基本步骤:
本方法步骤(1)、(2)与上述方法相同,在此不再重复介绍。
Table 1. The morphological parameter of evaluation object
表1. 评价对象的指标形态
(3) 构造加权系数矩阵
 (5)
(5)
确定出各指标的权重 ,以它们为主对角元素构造对角矩阵
,以它们为主对角元素构造对角矩阵 ,则
,则
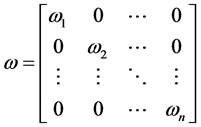 (6)
(6)
则,加权系数矩阵为:
 (7)
(7)
(4) 确定最优方案和最劣方案
最优方案每列中的最大值组成:
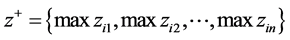 (8)
(8)
最劣方案每列中的最小值组成:
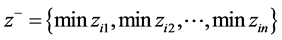
(5) 将正负理想解归一化,确定各评价指标的权重
正理想解权重:
 (9)
(9)
利用正理想解求得各评价指标的权重向量为:

负理想解权重为:
 (10)
(10)
利用正理想解求得各评价指标的权重向量为:

(6) 利用TOPSIS定权的模糊综合评判模型
将 转置并归一化得到各评价指标的评判矩阵为:
转置并归一化得到各评价指标的评判矩阵为:
 (11)
(11)
则由正负理想解确定的综合评向量分别为:
 (12)
(12)
将上述综合评判向量归一化,得到各向量组合的隶属度,根据最大隶属度原则,得到各参评企业的综合排序。
5. 实例分析
为了检验模糊综合评判方法结果的可行性,现采用常用的实例加以检验,将两者方法进行对比。已知医院的护理质量完成情况有8个指标,现在有2004~2008年的护理质量指标完成情况,现在运用TOPSIS模糊综合评价对其进行排序(见表2)。
表中:除X8是低优指标外,其余的都是高优指标;同趋性转变后,矩阵变为(见表3)。
采用TOPSIS-余弦法所得评价结果为(见表4)。
TOPSIS-余弦法和TOPSIS-模糊综合评价加权法的评价结果相同,则可以说明TOPSIS-模糊综合评价法能够用来进行综合评判,能够避免在评价过程中的人为定权的不合理性,为权重的计算提供了一个有一定数学基础的方法。
TOPSIS-模糊综合评判法结果为(见表5)。
6. 水文频率参数估计方法概述
(1) 矩法:矩法[1] 是用样本矩代替(或估计)总体矩,并通过矩和参数之间的关系式,来估计频率曲线统计参数的一种最简单参数估计法。矩法无需事先确定频率曲线线型,因而在洪水频率分析中广泛使用。
(2) 权函数法通过分析求矩差的产生原因,理想系列的求矩差,又称还原差。由两部分组成,一是有限和式代替积分,造成台阶形面积与曲边梯形面积之差,称为“梯矩差”。另一部分是用有限和代替无限区间上的积分,造成的“端矩差”。端矩差是求误差的主要部分。产生端矩差的总根源是系列短。对于项数相同的理想系列,端矩差的大小与经验频率公式的选择有关。通过引入正态分布函数作为权函数的权重,进行求解参数值。
(3) 数值积分单、双权函数法:单权函数法通过引入一个权函数提高皮尔逊III型频率曲线偏态系数Cs的计算精度。双权函数法是认为影响设计洪水精度的参数首先是均值和变差系数,其次才是偏态系数。通过引入第二个权重函数来提高变差系数的精度,采用数值积分公式计算权重函数矩,以提高计算精度。权函数法通过引进权函数和数值积分系数,改善了频率曲线和经验点据间的拟合,取得了良好的效果。但由于已有的数值积分系数是针对连续系列提出的,不便在通常遇到的不连续系列的参数计算中应用,限制了适用范围。
(4) 概率权重矩法:概率权重矩(Probability weighted moments, PWM)自提出以来,在水文界受到广泛的重视,
Table 2. Hospital nursing quality indicators
表2. 医院护理质量指标完成情况
Table 3. Convergence after transformation
表3. 趋同性变换后
Table 4. The evaluation result of the TOPSIS-cosine law
表4. TOPSIS-余弦法评价结果
国内众多学者的研究结果表明,PWM法是推求水文频率分布参数较为稳定的方法,其估计量具有良好的统计特性[10] -[12] 。20世纪90年代,国立爱尔兰大学博士Wang [13] 推广了PWM的概念,提出了部分概率权重矩(Partial probability weighted moments, PPWM),其利用低删失样本进行洪水频率分布参数估计,取得了较好的应用效果。文献[4] 将该方法推广应用于P-III型分布并推演出一套计算公式,表明这种方法也能应用于不能解析地表达成逆形式的分布,从而大大拓宽了它的应用范围。概率权矩法计算简便且具有许多优良的统计特性,比如,它能利用资料中更多的信息,避免计算高阶矩,成果较稳定等等。
7. 实际水文序列检验
本文利用文献[14] [15] 中提供的洪水序列,进行计算,计算结果如下表6、表7。从参数估计的结果我们可以看到五种参数估计方法对Pearson-III型曲线在拟合序列时所表现出来的差异之处。
计算结果分析:
(1) 表1、表2是两组容量不同的实际水文序列,两组排序结果相同,概率权重矩法的效果最优,矩法的计算效果最差。
(2) 矩法具有较大的端矩误差,因而评价结果在几组结果中效果排在最后;数值积分双权函数法的拟合效果优于数值积分单权函数法;权函数法的计算结果由于从减少端矩误差的角度出发,评价结果优于矩法。
Table 5. The evaluation result of the TOPSIS-fuzzy comprehensive evaluation
表5. TOPSIS-模糊综合评判法评价结果
Table 6. The evaluation result
表6. 评价结果
Table 7. The evaluation result
表7. 评价结果
8. 结论
(1) TOPSIS法对原始数据进行同趋势和归一化处理,消除了不同指标量纲的影响,排序结果充分利用原始数据信息,因而结果量化准确。它对评价对象没有特殊要求,既适用于小样本资料,也适用于多评价单元、多指标的大系统,应用灵活、实用性强。
(2) TOPSIS-模糊综合评判方法从定权的角度对评价结果进行分析,优于原来的人工定权中的不合理现象,具有严密的逻辑效果。
(3) 本研究在水文频率参数数值方法的对比分析基础上,采用了四种不同的评价标准,运用TOPSIS方法对评价指标进行定权,利用TOPSIS-模糊综合评判方法对几种常用的计算方法进行分析,评价结果与文献[16] 的结果相近。
致谢
水资源高效利用与保障工程河南省协同创新中心。
基金项目
河南省高校科技创新人才支持计划项目(13HASTIT034);华北水利水电大学研究生教育创新计划基金资助(YK2014-07)。
文章引用
雷冠军,王文川,刘 宽,邱 林, (2015) TOPSIS-模糊综合评判法在优选水文频率参数估计方法中的应用
The Application of the TOPSIS-Fuzzy Comprehensive Evaluation Method Used in the Method of Optimizing the Hydrologic Frequency Parameter Estimation. 水资源研究,02,200-207. doi: 10.12677/JWRR.2015.42024
参考文献 (References)
- 1. 水利部长江水利委员会. 水利水电工程设计洪水计算规范[S]. 北京: 水利水电出版社, 1993.
- 2. Ministry of Water Re-sources of the Yangtze River Water Resources Commission. Water resources and hydropower engineering specification design flood calculation. Beijing: China Water Power Press, 1993. (in Chinese)
- 3. 马秀峰. 计算水文频率参数的权函数法[J]. 水文, 1984, (3): 1-8.
- 4. MA Xiufeng. Calculation of hydrological frequency parameters of weight function method. Journal of China Hydrology, 1984, (3): 1-8. (in Chinese)
- 5. 刘光文. 皮尔逊III型分布参数估计[J]. 水文, 1990, (4): 1-15.
- 6. LIU Guangwen. Pearson type III distribution parameter estimation. Journal of China Hydrology, 1990, (4): 1-15. (in Chinese)
- 7. 宋德敦, 丁晶. 概率权重矩法及其在P-III分布中的应用[J]. 水利学报, 1988, (3): 1-11.
- 8. SONG Dedun, DING Jing. Probability weighted moment method and its application in P-III distribution. Journal of Hydraulic Engineering, 1988, 3(3): 1-11. (in Chinese)
- 9. 陈元芳, 沙志贵, 陈剑池, 陈民. 具有历史洪水时P-III型分布线性矩法的研究[J]. 水文, 2001, 29(4): 76-80.
- 10. CHEN Yuanfang, SHA Zhigui, CHEN Jianchi and CHEN Min. Study on L-moment estimation method for P-III distribution with historical flood. Journal of China Hydrology, 2001, 29(4): 76-80. (in Chinese)
- 11. 丛树铮, 谭维炎, 黄守信, 等. 水文频率计算中参数估计方法的统计试验研究[J]. 水利学报, 1980, (3): 1-14.
- 12. CONG Shuzheng, TAN Weiyan, HUANG Shouxin, et al. Statistical testing research on the methods of parameters estimation in hydrological computation. Journal of Hydraulic Engineering, 1980, (3): 1-14. (in Chinese)
- 13. HWANG, C. L., YOON, K. S. Multiple attribute decision making. Berlin: Spring-Verlag, 1981.
- 14. 郭靖, 郭生练, 胡安焱, 等. 基于TOPSIS法的水文模型多目标参数自动优选方法研究[J]. 水电能源科学, 2006, 24(6): 25-28.
- 15. GUO Jing, GUO Shenglian, HU Anyan, et al. Study on automatic parameter optimization of hydrological model using multi- objective function and TOPSIS. Water Resources and Power, 2006, 24(6): 25-28. (in Chinese)
- 16. 钱吴永, 党耀国, 熊萍萍, 等. 基于灰色关联定权的TOPSIS法及其应用[J]. 系统工程, 2009, 27(8): 124-126.
- 17. QIAN Wuyong, DANG Yaoguo and XIONG Pingping. TOPSIS based on grey correlation method and its application. Systems Engineering, 2009, 27(8): 124-126. (in Chinese)
- 18. DING, J., YANG, R. The determination of probability weighted moments with the incorporation of extraordinary values into sample data and their application to estimating parameters for the Pearson Type Three distribution. Journal of Hydrology, 1988, 101: 63-82.
- 19. 宋德敦, 丁晶. 概率权重矩法及其在p-III分布中的应用[J]. 水利学报, 1988, (3): 1-11.
- 20. SONG Dedun, DING Jing. Probability weighted moment method and its application in P-III distribution. Journal of hydraulic engineering.1988, (3): 1-11. (in Chinese)
- 21. LANDWEHR, J. M., MATALAS, N. C. and WALLIS, J. R. Probability weighted moments compared with some traditional techniques in estimating Gumbel parameters and quantiles. Water Resources Research, 1979, 15(5): 1055-1064.
- 22. WANG, Q. J. Estimation of the GEV distribution from censored samples by method of partial probability weighted moments. Journal of Hydrology, 1990, 120: 103-114.
- 23. 王文川, 邱林, 徐冬梅, 陈海涛. 工程水文学[M]. 北京: 中国水利水电出版社, 2013.
- 24. WANG Wenchuan, QIU Lin, XU Dongmei and CHEN Haitao. Engineering hydrology. Beijing: China Water Power Press, 2013. (in Chinese)
- 25. 宋孝玉, 马细霞. 工程水文学[M]. 郑州: 黄河水利出版社, 2009.
- 26. SONG Xiaoyu, MA Xixia. Engineering hydrology. Zhengzhou: The Yellow River Water Conservancy Press, 2009. (in Chinese)
- 27. 葛吉琦. 用威布尔分布进行水文频率计算的探讨[J]. 人民长江, 1990, (2): 18-25+17.
- 28. GE Jiqi. Weibull distribution in hydrological frequency calculation. Yangtze River. 1990, (2): 18-25+17. (in Chinese)
