Statistics and Application
Vol.05 No.02(2016), Article ID:17935,11
pages
10.12677/SA.2016.52020
Price Forecasting and Risk Control Model of Copper Futures Based on Markov State Transition Model
Yongzhong Tian
Yunnan Copper Industry Limited by Share Ltd., Kunming Yunnan

Received: Jun. 9th, 2016; accepted: Jun. 25th, 2016; published: Jun. 30th, 2016
Copyright © 2016 by author and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
Copper as a kind of important non-ferrous metals, has a strong influence on other non-ferrous metal prices, so the stable development of the copper futures market not only has an important role in spot copper market development, but also has great significance in other non-ferrous metals market stability and promoting sound and rapid development of the national economy. In this paper, the two-state Markov state transformation model is used to predict the yield and volatility of copper futures with good results.
Keywords:Copper Futures, Markov Transformation Model, Composite Likelihood Function

基于Markov状态转换的期货铜价格预测及风险控制模型
田永忠
云南铜业股份有限公司,云南 昆明

收稿日期:2016年6月9日;录用日期:2016年6月25日;发布日期:2016年6月30日

摘 要
铜作为一种重要的有色金属,对其他有色金属的价格具有较强的影响力,因此期货铜市场的稳定发展不仅对现货铜市场具有重要作用,同时对其他有色金属市场的稳定,促进国民经济的又好又快发展,都具有重大意义。本文运用两状态的Markov状态变换模型对期货铜的收益率和大幅波动情况进行了预测,取得了良好的效果。
关键词 :铜期货,Markov态变换模型,复合似然函数

1. 引言
铜作为一种重要的工业重金属,被广泛地应用于电气、轻工、机械制造、建筑工业等领域,在国民经济的发展中有着重要的地位。但是,自2008年金融危机以来,铜的价格波动十分频繁,给铜的生产和销售环节带来了巨大的风险,对我国经济的平稳运行产生了巨大的冲击。因此,对于铜的价格和波动预测具有十分重要的理论和现实意义。
Markov状态换模型由Hamilton (1989) [1] 首先提出,他在研究美国的经济周期时,运用三状态两阶滞后的Markov机制转换模型研究了美国1953~1984年间季度实际产出增长的波动,模型回归效果良好。Cai (1994) [2] 、Hamilton、Susmel (1994) [3] 几乎同时提出了将Markov状态换模型引入ARCH模型中的方法,这一创举使得对变结构金融资产序列的波动性建模取得了显著的进步和发展。孙金丽、张世英(2003) [4] 将MS-GARCH模型运用到中国股票市场的分析中,证明具有结构转换功能的MS-GARCH模型的分析结果由于单一状态条件下的GARCH模型。朱钧钧 [5] (2011)利用马尔科夫状态转换–门限GARCH模型的MCMC估计对我国股市波动率的双重不对称性进行了解释,得到了稳定并且可信的结果。
本文共分为以下几个部分:第一章、前言,介绍本文的背景、框架和内容;第二章、理论方法综述,介绍本文所采用方法的相关理论介绍;第三章、模型分析,介绍模型的分析结果,重点分析模型的收益率、涨跌方向预测准确率、大幅波动的预测情况;第四章、模型的缺陷和不足,介绍模型中仍存在的缺陷和未来改进的方向;第五章、总结,对分型进行概括和总结。
2. 理论方法综述
2.1. Markov链
设随机过程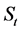 只取整数值
只取整数值 ,假定,
,假定, 的取值只与
的取值只与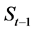 有关,而与t − 1期前S的取值无关,那么此随机过程被称为N状态下的马尔科夫链,用公式可表示为:
有关,而与t − 1期前S的取值无关,那么此随机过程被称为N状态下的马尔科夫链,用公式可表示为:
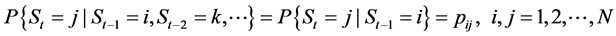
转移概率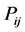 代表状态
代表状态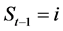 条件下
条件下 的概率,若该过程服从一阶Markov链过程,可用转移矩阵P来表示转移概率:
的概率,若该过程服从一阶Markov链过程,可用转移矩阵P来表示转移概率:
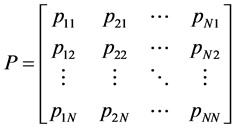
其中, ,
,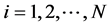 。
。
2.2. Markov模型
下面以正态分布为例,构建期货黄金指数的Markov模型,假定t时期的期货黄金指数为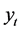 ,
, 。假定存在一个不可观测变量
。假定存在一个不可观测变量 代表t时刻期货黄金指数所处状态,当
代表t时刻期货黄金指数所处状态,当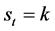 ,
, 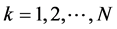 ,
,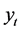 的边缘分布为
的边缘分布为 ,
, 服从N状态下的一阶马尔科夫链。
服从N状态下的一阶马尔科夫链。
Markov模型中需要估计的参数有转移概率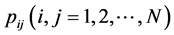 ,
,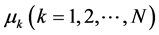 ,
,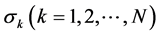 。我们采用EM算法去进行参数估计,关于似然函数的选择有两种方式:完全似然函数Zucchini (2009) [6] 、复合似然函数Zou (2013) [7] 。不过在Zou (2013) [7] 已经说明复合似然函数效果要好于完全似然函数。
。我们采用EM算法去进行参数估计,关于似然函数的选择有两种方式:完全似然函数Zucchini (2009) [6] 、复合似然函数Zou (2013) [7] 。不过在Zou (2013) [7] 已经说明复合似然函数效果要好于完全似然函数。
在正态分布条件下,复合似然函数可表示为:

其中,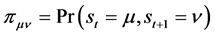 表示
表示 时刻为
时刻为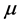 状态而
状态而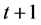 状态。
状态。 表示
表示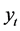 属于状态μ状态的概率。
属于状态μ状态的概率。
每时刻的状态都是未知的,我们可以将其作为缺失变量。因此可以利用EM算法估计参数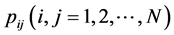 ,
,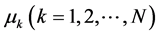 ,
,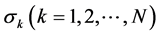 。利用所预测出来的参数,通过平滑概率,可以计算出当t = T时,
。利用所预测出来的参数,通过平滑概率,可以计算出当t = T时,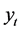 属于每个状态的概率。我们也可以通过参数P、
属于每个状态的概率。我们也可以通过参数P、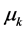 、
、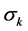 与第t时刻的观测值
与第t时刻的观测值 可以预测出当
可以预测出当 时,
时, 属于每个状态的概率,均值和方差。
属于每个状态的概率,均值和方差。
本文运用惩罚下复合似然函数Chen (2012) [7] 作为似然函数
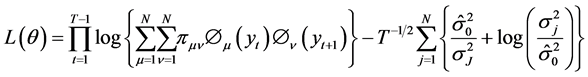
在这里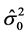 为序列的样本方差。由Zou (2013) [7] 可知在这种方法下迭代步骤分为E-STEP和M-STEP两个步骤:
为序列的样本方差。由Zou (2013) [7] 可知在这种方法下迭代步骤分为E-STEP和M-STEP两个步骤:
在E-STEP,我们运用贝叶斯公式计算条件期望值
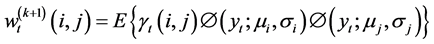
其中 。在EM算法中,我们假定这个变量为隐藏变量。
。在EM算法中,我们假定这个变量为隐藏变量。
在M-STEP,我们最大化似然函数,则可得:
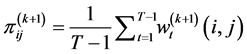 ,
,

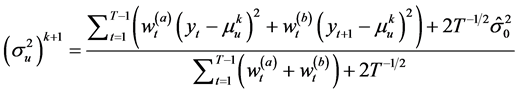 ,
,
其中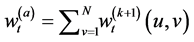 和
和 ,其中
,其中 。
。
3. 模型分析
本章我们将利用Markov状态转换模型对2001年1月2日至2015年12月21日的上海期货铜指数日收益率进行分析。我们利用过去交易日的数据结合Markov状态转换模型对下一交易日上海期货铜指数日收益率进行预测,分别预测出下一交易日上海期货铜指数日收益率的均值、方差、上涨(下跌)概率,并结合前一交易日的持仓量和交易量对下一交易日大幅波动的情况进行预测
3.1. 日收益率数据分析
我们使用上海期货铜指数日收益率作为研究对象,在这里我们用指数益率作为收益率的代表,令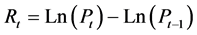 ,其中,
,其中, 代表第t天上海期货铜指数的收盘价,为此我们可以得到关于日收益的时间序列图,见图1所示。
代表第t天上海期货铜指数的收盘价,为此我们可以得到关于日收益的时间序列图,见图1所示。
可以看出,2001年~2015年上海期货铜日收益率大都在0附近徘徊,同时,收益率存在着一定的波动聚集性,这主要是指在金融时间序列中,一个较大的波动后往往会跟着一个较大的波动,而一个较小的波动后往往跟着一个较小的波动,这反映的是金融波动的正相关性和正反馈效应。因此,通过过去一个

Figure 1. 2001~2015 Shanghai futures copper’s daily index return rate
图1. 2001~2015年上海期货铜日指数收益率
时间段上海期货铜的日交易数据对下一交易日上海期货铜的日收益率进行预测具有一定的合理性。
3.2. 模型构建
我们利用Markov状态转换模型对上海期货铜的日指数收益率进行分析,构建模型。我们假定每一个交易日的上海期货铜的指数收益率服从正态分布,且在训练期间内,上海期货铜的指数收益率存在两种波动状态,即上海期货铜的指数收益率服从两个不同的正态分布,且两种状态之间的转换过程服从一阶马尔可夫过程。
此时,复合似然函数可表示为:
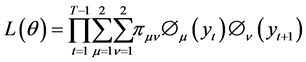
其中, 。
。
通过复合似然函数,利用EM算法,可以估算出转移概率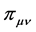 ,
,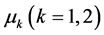 ,
,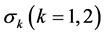 。利用预测出来的参数,通过平滑概率,可以计算出当t = T时,
。利用预测出来的参数,通过平滑概率,可以计算出当t = T时,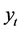 属于每个状态的概率,再结合转移概率
属于每个状态的概率,再结合转移概率 ,可以预测出当
,可以预测出当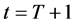 时,
时, 属于每个状态的概率,通过状态参数
属于每个状态的概率,通过状态参数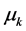 、
、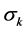 可以预测数
可以预测数 的均值和方差,通过均值和方差,我们可以计算出
的均值和方差,通过均值和方差,我们可以计算出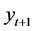 大于或小于0的概率(即上涨或下跌的概率)以及
大于或小于0的概率(即上涨或下跌的概率)以及 大于0.02或小于−0.02大概率(即出现大幅波动的概率)。
大于0.02或小于−0.02大概率(即出现大幅波动的概率)。
3.3. 模型效果
我们通过以下3个方面来衡量Markov状态转换模型的分析效果,一、模型的收益率情况,二、模型预测的准确率情况,三、模型对大幅波动的预判情况。
关于模型训练区间的选取并没有特定的标准,由于模型当中需要估计6个参数,训练区间不宜选取太短;同时,由于假定上海期货铜的指数收益率存在两种波动状态,训练区间不宜选取太长。为此,我们分别考虑100个交易日、150个交易日、200个交易日的情况。
3.3.1. 模型的收益率
为了考察模型的收益率,我们按照模型预测出上涨或下跌的概率进行投资,当上涨概率大于50%时买入,上涨概率小于50%时卖出,模型2001年1月21日~2015年10月21日的收益率如表1所示,在3种不同训练期间情况下,模型的平均收益率均在10%以上,在训练期间等于150个交易日时,平均收益最高为18.16%。
3.3.2. 模型的准确率
为了考察模型的收益率,我们依然考查的是通过Markov状态转换模型预测出的下一交易日上涨或下跌的概率,我们设定一个阈值Ɵ (Ɵ ≥ 0.5),当上涨(下跌)概率 ≥ Ɵ时,我们认为下一交易日存在上涨(下跌),然后,我们将实际情况与我们的预测情况进行比较,分析模型的预测准确率。图2~图4所示为Ɵ在0.5~0.6时,模型预测的准确率的情况。
Table 1. 2001~2015 three model yields
表1. 2001~2015三种模型收益率情况
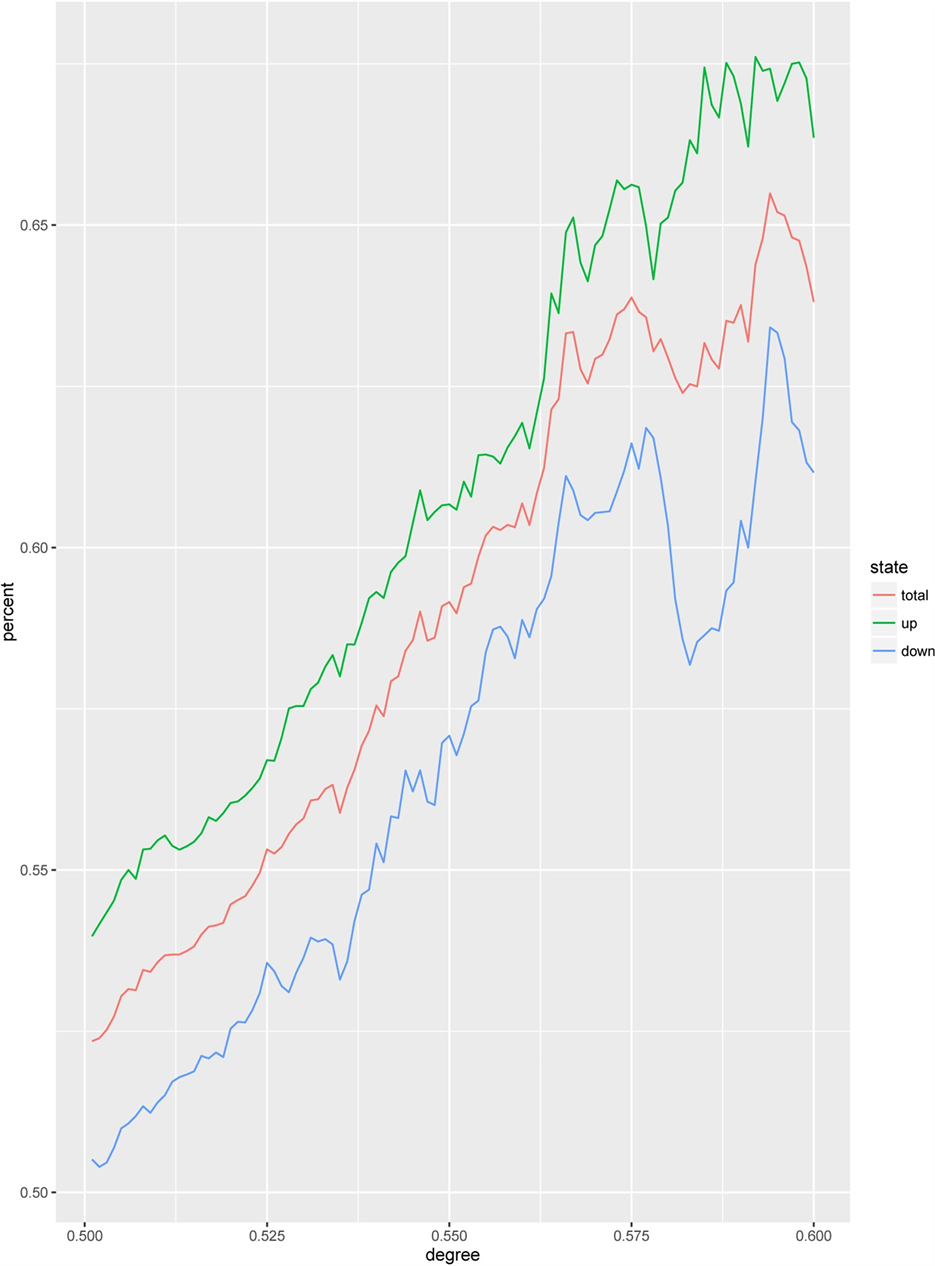
Figure 2. Prediction accuracy of the model (training time equals 100 trading days)
图2. 训练期间为100个交易日时模型的预测准确率
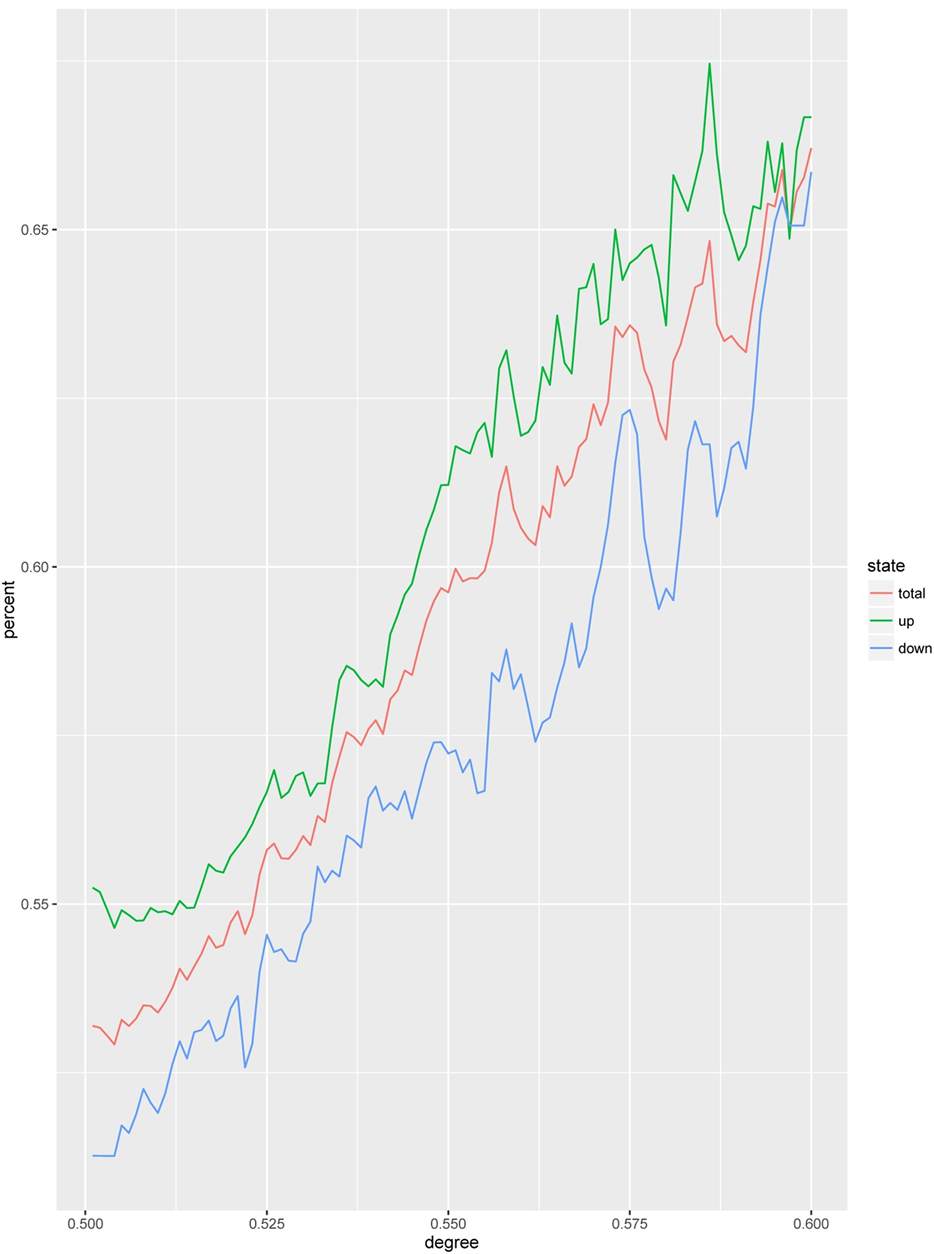
Figure 3. Prediction accuracy of the model (training time equals 150 trading days)
图3. 训练期间为150个交易日时模型的预测准确率
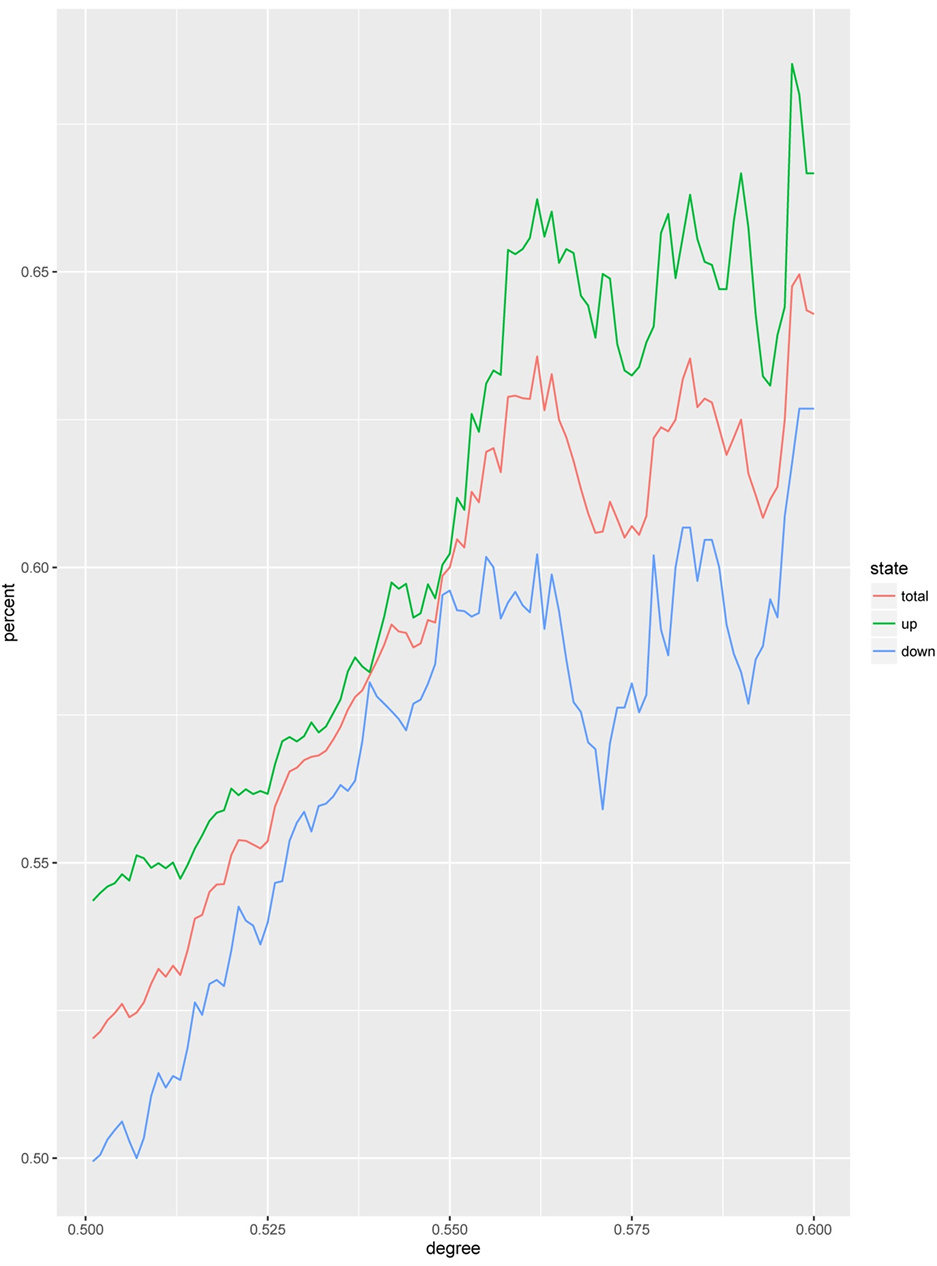
Figure 4. Prediction accuracy of the model (training time equals 200 trading days)
图4. 训练期间为200个交易日时模型的预测准确率
可以发现,模型对下一交易日上涨行情的预测要优于下跌行情的预测,但随着阈值的不断提高,无论是总体预测准确率还是上涨行情和下跌行情的准确率都不断提高,最终模型预测的总体准确率都在60%以上。
3.3.3. 模型对大幅波动的预判
为了考察模型对大幅波动的预判,我们运用预测出的下一交易日收益均值、方差、以及由此计算出的下一收益率的绝对值大于2%的概率、前一交易日的交易量和持仓量,通过随机森林模型对下一交易日收益率的绝对值大于2%的情况进行预测。
我们以训练期间为150交易日的模型为例,训练集选用2014年前150个交易日,测试集为2014年8月13日~2015年10月21日。表2所示为模型对测试集大幅波动预测的情况。
可以发现,模型对大幅波动的预测准确率为65.22%,整体准确率为85.2%,表明利用预测出的下一交易日收益均值、方差、以及由此计算出的下一收益率的绝对值大于2%的概率、前一交易日的交易量和持仓量等信息可以在一定程度上对下一交易日的大幅波动进行预警。
4. 模型的缺陷和不足
虽然模型在收益率、准确率和大幅波动的预警等方面表现良好,同时值得注意的是,模型当中依然存在着一些不足,例如,我们模型中假设上海期货铜的指数收益率服从正态分布,但金融数据中往往存在着“尖峰厚尾”的情况,我们的模型会在一定程度上低估模型的风险。如图5所示,我们模型预测出的收益率较实景情况中的收益率更多的集中在0附近,对大幅波动的预测存在一定的偏差。为此,模型可以通过将正态分布调整为t分布来更好地拟合这一情况。
5. 总结
本论文建立了两状态的马尔可夫转换模型,同时利用复合似然函数方法以及EM算法来对铜期货的数据进行模拟预测,模型的分析结果良好,同时模型具有以下优势:
第一,模型的收益率良好。我们用模型对过去100天,150天和200天的交易日的数据进行训练,对下一交易日收益率大于0的概率进行预测,利用这个概率进行投资,从2001~2015年15年的交易数据来看,3个模型的年平均收益率均在10%以上,以150个交易日为训练期间的模型表现最为良好,模型的年平均收益率为18.16%。
第二,模型的准确率比较高。随着阈值的不断提高,模型的准确率也不断上升,从最初的百分之五十左右一直上升到了百分之六十之上,也就是说通过这个马尔可夫模型预测出来的第二天涨跌的概率具有一定的实际和理论分析意义。
第三,同时我们利用随机森林的方法,结合通过马尔可夫模型预测出的下一交易日收益均值、方差、以及由此计算出的下一收益率的绝对值大于2%的概率、前一交易日的交易量和持仓量,对第二天波动幅度超过2%的情况的预测。我们利用2014年前150个交易日,预测2014年8月13日~2015年10月21日的交易
Table 2. The predict situation of model to large fluctuations
表2. 模型对大幅波动的预测情况
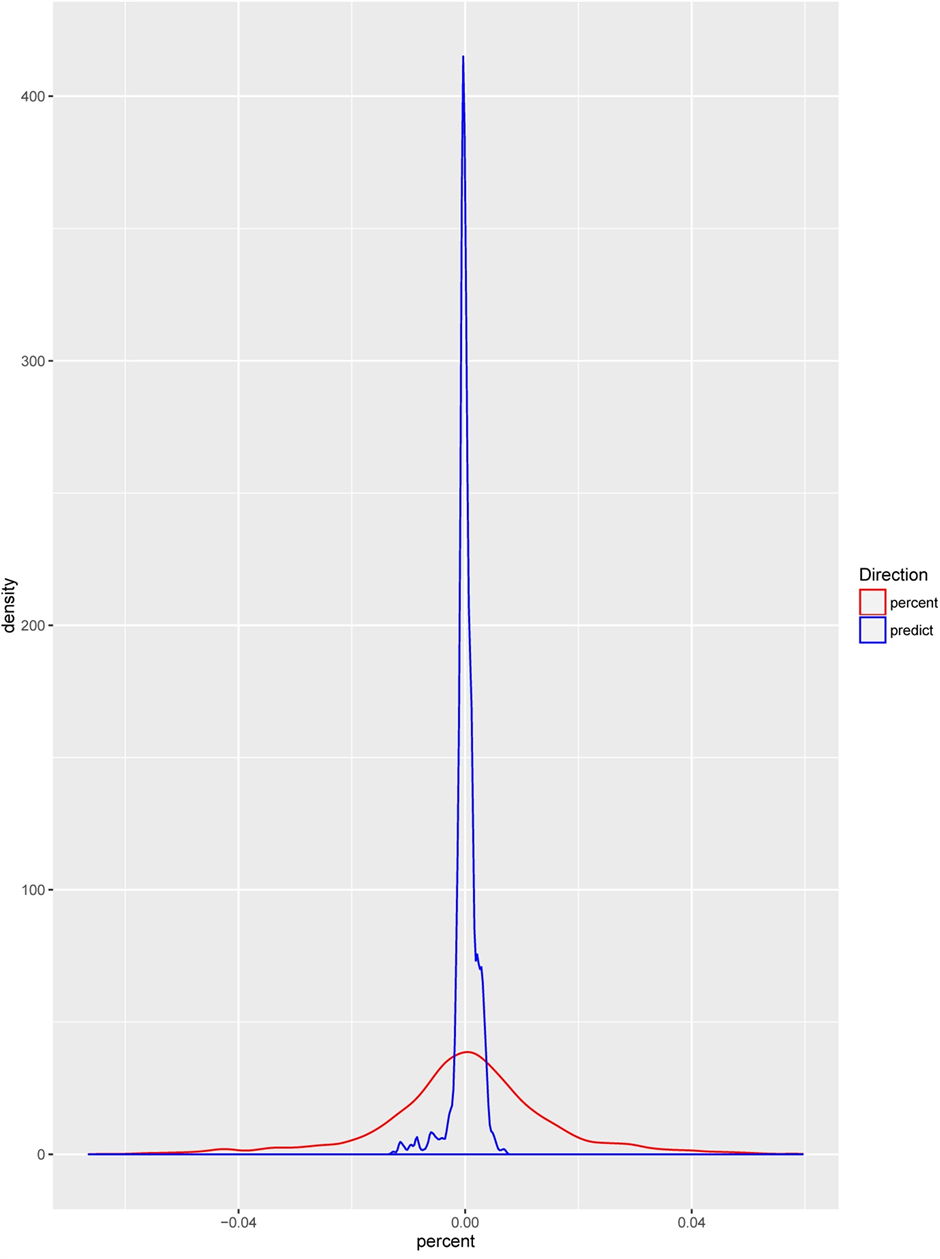
Figure 5. Comparison of actual yield and forecast yield
图5. 实际收益率与预测收益率比较
情况,预测结果表示,模型可以准确的预测出其中65.22%的大幅波动情况,因此,我们可以认为这个模型对出现大幅波动的预测情况良好。
但值得注意的是,模型依然存在着一定的缺陷,由于我们的模型假设是正态分布,通过图5可以看出,通过模型所预测出来的大部分收益率的波动情况跟实际情况而言较窄,也就是说我们的模型在一定程度上低估实际情况中期货市场的各种风险。由于低估了这些风险,会使得我们的模型对第二天收益率的估计造成一定的风险。我们可以通过将模型假设改为t分布或其他的厚尾分布从而改进这个模型。
综上所述,虽然这个模型有着一定的缺陷,但是该模型的收益率良好,准确率也达到了百分之六十以上,同时对期货市场出现大幅波动的预测结果良好,我们可以认为这个模型在预测铜期货的收益率有着一定的实际用处,同时可以根据所预测出来的大幅波动来对市场的投资进行一定的调整。
文章引用
田永忠. 基于Markov状态转换的期货铜价格预测及风险控制模型
Price Forecasting and Risk Control Model of Copper Futures Based on Markov State Transition Model[J]. 统计学与应用, 2016, 05(02): 203-213. http://dx.doi.org/10.12677/SA.2016.52020
参考文献 (References)
- 1. Hamilton, J.D. (1989) A New Approach to the Economic Analysis of Nonstationary Time Series and the Business Cycle. Economet-rica, 57, 357-384. http://dx.doi.org/10.2307/1912559
- 2. Cai, J. (1994) A Markov Model of Switching-Regime ARCH. Jour-nal of Business and Economic Statistics, 12, 309- 316.
- 3. Hamilton, J.D. (1994) Analysis of Time Series Subject to Changes in Regime. Journal of Econometrics, 45, 39-70. http://dx.doi.org/10.1016/0304-4076(90)90093-9
- 4. 孙金丽, 等. 具有结构转换的GARCH模型及其在中国股市中的应用[J]. 系统工程, 2003, 21(6): 86-91.
- 5. 朱钧钧, 谢识予. 中国股市波动率的双重不对称性及其解释[J]. 金融研究, 2011(3): 134-148.
- 6. Zucchini, W. and MacDonald, I.L. (2009) Hidden Markov Models for Time Series: An Introduction Using R. CRC Press, New York. http://dx.doi.org/10.1201/9781420010893
- 7. Zou, W. and Chen, J.H. (2013) A Markov Regime-Switching Model for Crude-Oil Markets: Comparison of Composite Likelihood and Full Likelihood. The Canadian Journal of Statistics, 2, 353-367. http://dx.doi.org/10.1002/cjs.11173
- 8. Chen, J. and Wang, P. (2012) Composite Likelihood Approach for the Analysis of Exchange Rates. Working Paper.
