Statistics and Application
Vol.07 No.02(2018), Article ID:24590,7
pages
10.12677/SA.2018.72022
Analysis and Forecast of the Energy Price Index Based on ARIMA Model
Yanwen Yan
College of Science, China University of Petroleum, Beijing

Received: Apr. 2nd, 2018; accepted: Apr. 20th, 2018; published: Apr. 27th, 2018

ABSTRACT
In this paper, the monthly international market energy price index of 2000-2017 year is used as the raw data. Through the series of data processing, the ARIMA(1,1,0) model is established. And the international market energy price index time series of the changes in the performance of the law is expounded; the international market energy price index for the next 12 months is forecasted. The test results show that the model can make a short-term reasonable prediction for the future, and can give decision-making reference for economic development goals.
Keywords:ARIMA Model, Index, Non-Stationary, Prediction
基于ARIMA模型的能源价格指数分析与预测
严彦文
中国石油大学(北京)理学院,北京

收稿日期:2018年4月2日;录用日期:2018年4月20日;发布日期:2018年4月27日

摘 要
本文以世界2000~2017年每月国际市场能源价格指数为原始数据,通过对数据的处理,建立ARIMA(1,1,0)模型。从而阐述国际市场能源价格指数时间序列所表现的变化规律,对国际市场能源价格指数进行了未来12个月的预测。检验结果表明该模型对未来能够做出合理的短期预测,进而为制定经济发展目标提供决策参考。
关键词 :ARIMA模型,指数,非平稳,预测

Copyright © 2018 by author and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
ARIMA模型全称为求和自回归移动平均模型(Autoregressive Integrated Moving Average Model),简记ARIMA,是由博克思(Box)和詹金斯(Jenkins)提出的著名时间序列预测方法,称为Box-Jenkins模型。其中ARIMA(p,d,q)称为求和自回归移动平均模型,AR是自回归,p是自回归项数,MA为移动平均,q为移动平均项数,d为时间序列成为平稳是所做的差分次数。所谓ARIMA模型,是指将非平稳时间序列转化为平稳时间序列,然后将因变量仅对它的滞后值以及随机误差项的现值和滞后值进行回归所建立的模型 [1] 。
国际能源消费格局面临调整,消费重心转移,亚太市场成为各大原油出口国争夺的焦点。亚洲及大洋洲的石油消费量已占全球32.7%,而北美和欧洲地区分别占23.9%和18.5%。亚太市场特别是中、印还是目前全球仅有的原油需求处于大量增长中的地区。各大原油出口国已经将目标转向亚太,积极扩大在此地区的市场份额。沙特2016年9月已将发往亚洲的轻质油等原油种类价格下调,对亚洲市场“特殊照顾”,积极争夺亚洲客户;伊朗自解禁后开始加大对亚洲的原油出口,近几个月已将大量原油出售给中国、印度和韩国等亚洲买家;而伊拉克2016年二季度靠重质原油价格打折首超沙特成为印度最大原油供应国。国际能源消费重心正逐渐向亚太转移,国际能源消费格局也将进入新的调整期 [2] 。
本文通过使用ARIMA模型对近20年内国际能源价格进行详细分析其发展趋势,并预测其未来12个月的发展展望。
2. 理论基础
拿到一个观察值序列之后,首先对它的平稳性和纯随机性进行检验,这两个检验称之为时间序列的预处理。根据不同的检验结果将序列分为不同的类型,进而采用不同的分析方法。
2.1. 平稳性检验
对随机时间序列进行平稳性检验是非常必要的。本文主要基于SAS 软件采用时序图检验和自相关图检验。
2.2. 纯随机性检验
对于随机序列 ,如果 , ; , ,则称 为纯随机序列,又称为白噪声序列。白噪声是平稳的随机过程,是一种没有分析价值的序列。
如果一个时间序列是纯随机的,得到一个观察期数为n的观察值序列{ },那么该序列的延迟非零期的样本自相关系数将近似服从均值为零、方差为序列观察期数倒数的正态分布,即

式中n为观察期数。下面来检验序列的纯随机性。
原假设和备择假设分别为:原假设: ;
备择假设:至少存在某个 。检验统计量为LB检验统计量:
当 统计量的真值大于程 分位点,或该统计量的P值小于 时,则以 的置信水平拒绝原假设,认为该序列为非纯随机序列;否则,接受原假设,认为该序列为纯随机序列。
2.3. ARIMA模型
具有如下结构的模型称为求和自回归移动平均(Autoregressive Integrated Moving Average)模型,简记为ARIMA(p,d,q)模型 [3] :
式中 , ,为平稳可逆ARMA(p,q)模型的自回归系数多项式; ,平稳可逆ARMA(p,q)模型的移动平滑系数多项式。
ARIMA(p,d,q)模型中参数d是非平稳时间序列经过差分的次数。从理论上讲,足够多次的差分运算可以充分地提取序列中的非平稳确定性信息,但差分运算的阶数并不是越多越好。因为差分运算是一种对信息的提取、加工过程, 每次差分都会有信息的损失,所以在实际应用中差分运算的阶数要适当,应当避免过差分的现象。
ARIMA(p,d,q)模型的实质是差分运算与ARMA模型的结合,具有较高的短期预测精度,且不需要数据具有较强的结构性,只需要从数据本身寻找规律,并能较好的拟合数据。
3. 实例分析
ARIMA模型建模遵循如下流程图:

1) 运用国际市场能源价格指数数据,基于SAS软件绘制其时序图 [4] :
时序图1显示,该序列有显著的趋势,为典型的非平稳序列。
2) 对原序列进行差分运算
因为原序列呈现出近似线性趋势,所以选择1阶差分。1阶差分后序列时序图如下图2所示:

Figure 1. The sequence diagram of the international market energy price index from January 2000 to March 2017 year
图1. 2000年1月~2017年3月国际市场能源价格指数时序图

Figure 2. The sequence diagram of the first order difference of the energy price index from January 2000 to March 2017 year
图2. 2000年1月~2017年3月能源价格指数1阶差分后序列时序图
时序图2显示,差分后序列明显表现出平稳的特性。为了进一步确定平稳性,考察差分后序列的自相关图:
自相关图3显示序列有很强的短期相关性,结合差分后的时序图可以认为差分后序列平稳。
3) 对平稳的1阶差分序列进行白噪声检验
应用SAS软件,得到一阶差分后序列白噪声检验的P值,见表1。
由表1可见,在检验的显著水平0.05的条件下,由于延迟6阶和12阶的 检验统计量的P值小于0.05,所以该差分后序列不能视为白噪声序列,即差分后序列还蕴含着不能忽视的相关信息可供提取。
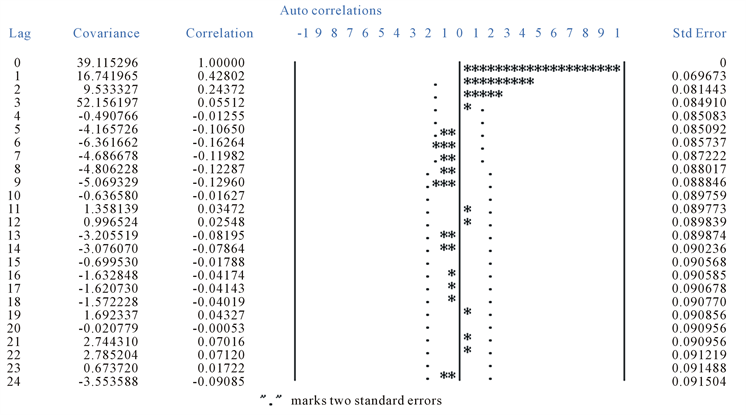
Figure 3. The diagram of autocorrelation of the first order difference of the energy price index series
图3. 能源价格指数1阶差分后序列自相关图
Table 1. The test of white noise of the first order difference of the energy price index series
表1. 能源价格指数1阶差分后序列白噪声检验
Table 2. The parameter estimation of the first order difference of the energy price index series
表2. 能源价格指数1阶差分后序列拟合模型参数估计
4) 对非平稳非白噪声差分序列拟合ARMA模型
一阶差分后的序列自相关系数函数拖尾,偏相关系数函数截尾,原序列的拟合模型为ARIMA(1,1,0),模型口径为: ,其中参数估计采用条件最小二乘估计,参数估计值有表2给出。
5) 预测结果
通过国际市场能源价格指数,即2000年1月~2017年3月以来的数据进行分析后,对其进行将来12个月的预测,预测结果如下(表3)。
图4显示,随着预测时期的增长,预测误差越大,预测区间呈现为喇叭形,这是时间序列预测的典型特点。
Table 3. The prediction value of the fitting model ARIMA(1,1,0)
表3. 拟合模型ARIMA(1,1,0)的预测值
 说明:图中星号为序列观察值;中间曲线为序列预测值;上下曲线为95%的置信区间。
说明:图中星号为序列观察值;中间曲线为序列预测值;上下曲线为95%的置信区间。
Figure 4. The prediction diagram of the energy price index series
图4. 能源价格指数序列预测图
4. 总结
通过对2000年1月~2017年3月国际市场能源价格指数数据分析,建立了ARIMA(1,1,0)模型,并预测了未来国际能源价格指数将来的发展趋势,发现价格变动非常小,价格稳定增长且增长非常缓慢。通过对国际能源价格指数的分析,可以进一步分析国际能源价格指数的变化对各个国家的经济影响趋势。
基金项目
中国石油大学(北京)基础科研基金项目(编号:2462012KYJJ0609);中国石油大学(北京)教学研究项目(编号:21G16097)。
文章引用
严彦文. 基于ARIMA模型的能源价格指数分析与预测
Analysis and Forecast of the Energy Price Index Based on ARIMA Model[J]. 统计学与应用, 2018, 07(02): 176-182. https://doi.org/10.12677/SA.2018.72022
参考文献
- 1. 王燕. 时间序列分析[M]. 第四版. 北京: 中国人民大学出版社, 2016.
- 2. 唐炼. 世界能源供需现状与发展趋势[J]. 国际石油经济, 2005(1): 30-33.
- 3. 区诗德, 覃思乾. 基于60分钟线的ARIMA模型分析日K线走势[J]. 统计与决策, 2005, 12(24): 145-146.
- 4. 高惠璇, 等. SAS系统SAS/ETS软件使用手册[M]. 北京: 中国统计出版社, 1998.
