Statistics and Application
Vol.
08
No.
02
(
2019
), Article ID:
29721
,
7
pages
10.12677/SA.2019.82034
Quantitative Stock Picking Model Based on Conditional Random Fields
Yusi Zhang, Manfa Liang
School of Mathematics, South China University of Technology, Guangzhou Guangdong
Received: Mar. 25th, 2019; accepted: Apr. 9th, 2019; published: Apr. 16th, 2019

ABSTRACT
As a special Conditional Random Field model, the Hidden Markov Model is one of the secret weapons behind the brilliant performance of the medallion fund. From the perspective of financial engineering, this paper introduces the Hidden Markov Model into the investment field to predict the future rising and falling situation of individual stocks. Assuming that each of the ups and downs has a clear pattern, which can be described by an HMM model, if the probability of a stock's observation on the HMM model characterizing the rising pattern is greater, the probability that the stock actually rises is also the bigger. Based on the HMM model, the HMM factor of individual stocks was constructed, and the empirical analysis of the historical back testing of the Shanghai and Shenzhen 300 constituent stocks from 2016 to 2018 achieved a good excess return, which indicated that the conditional random field introduced into the quantitative stock selection has a predictive ability.
Keywords:Conditional Random Field, Financial Engineering, HMM, Rising Pattern
基于条件随机场的量化选股模型
张宇思,梁满发
华南理工大学数学学院,广东 广州
收稿日期:2019年3月25日;录用日期:2019年4月9日;发布日期:2019年4月16日

摘 要
作为特殊的条件随机场模型的隐马尔可夫模型是大奖章基金辉煌业绩背后的秘密武器之一,本文从金融程的角度出发,将隐马尔可夫模型引入到投资领域来预测个股未来的涨跌情况。假设涨和跌的股票各自都存在一种明确的模式,都分别可由一个HMM模型来描述,那么如果一个股票在表征上涨模式的HMM模型上的观测条件概率越大,说明该股票实际上涨的概率也越大。基于HMM模型构建了个股的HMM因子,并在沪深300成分股中通过在2016年到2018年历史回测的实证分析取得了不错的超额收益,从而说明条件随机场引入到量化选股中具有一定的预测能力。
关键词 :条件随机场,金融工程,隐马尔可夫模型,上涨模式

Copyright © 2019 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
股票市场的不确定性和不稳定性产生了庞大而且复杂的股票数据,其背后隐藏着众多有效的股票信息,挖掘出背后的价值能够帮助企业在分析企业的相关情况后有效地改变策略来提升竞争力,获得更好的形象特征。本文将统计中的条件随机场模型引入到投资中,从而构建出基于统计模型的量化投资策略。
文献 [1] 提出了一种近似的组合技术方法构建混合模型,通过数据简约,竞争学习以及改进的期望最大化算法估计模型中的参数,利用贝叶斯规则将象元分到适当的区域中,从而完成分割。文献 [2] 探讨了结合高斯有限混合模型与期望法,取得了很好的分割效果。郭松涛等人 [3] 提出一种改进的小波域隐马尔可夫树模型,用于分割遥感图像,该法在降低了算法的时间复杂度的同时,也取得了很好的分割结果。文献 [4] 提出了一种基于广义模糊Gibbs随机场模型理论,并将高阶邻域空问约束信息引入其中,为图像分割提供了一种新的思路。Lei Zhang,Qiang Ji [5] 使用统一概率图模型来分割图像,将贝叶斯网络和条件随机场模型通过因子图组合成一个分割整体框架,取得了比较好的分割结果,为图像分割提供了一个新途径。同时 [6] 使用贝叶斯网络自动和交互的分割图像,当面对比较复杂的图像时,使用自动分割效果,如果不理想,可以使用交互的方式对分割目标进一步分割,直至满意为止。
本文将语音识别的技术引入到股票涨跌预测中。假设上涨和下跌的股票各自都存在一种明确的模式,都分别可由一个HMM模型来描述。我们选择沪深300成分股的换手率、股价1日涨跌幅等6个价量指标作为模型观测值,选择股票池内上涨与下跌的样本训练表征上涨与下跌模式的HMM模型,通过构造出“上涨”条件因子进行选取,通过历史回测,取得了不错的投资效果。
2. 隐马尔可夫模型
2.1. 基本假设
由于马尔可夫模型在许多应用中有局限,人们通过扩展提出了更有代表性的模型,叫做隐马尔可夫模型(HMM)。在HMM中,我们并不知道什么产生观测序列的。状态的数目,转移概率以及产生观测的状态是未知的。HMM的每一个状态与概率函数联系而不是将每一个状态与确定的输出结合。在时刻 ,一个观察 由概率函数 产生,它与状态 有关,产生概率为:
(1)
一个HMM包含5个元组: :
1) 为状态集合,在时刻 的状态定义为 ,
2) 为输出字母,在离散的观测密度下, 是观测可选择的数目,
3) 初始状态分布 。 定义为
(2)
4) 状态转移概率分布
(3)
5) 观测符号概率分布 。对于每一个状态 产生观测的概率函数为:
(4)
用HMM对问题进行建模后,并假设HMM通过生成了一组数据,我们能够计算观察序列的概率和可能的潜在状态序列。我们也可以根据观测数据来训练模型参数并获得更加精确的模型,然后用训练的模型来预测未知数据。
2.2. 前向算法
给定一个模型 以及观测序列 ,我们怎样有效计算给定模型中观测序列的概率,即 。
定义前向变量 为:
(5)
保存在给定观测序列 时刻 状态为 的总概率。它是通过对网格节点处所有传入弧的概率求和来计算的。在每一个时刻 的前向变量能够通过归纳法计算,流程如下:
1) 初始化:
(6)
2) 归纳:
(7)
3) 更新时间 ;如果 返回第2步;否则终止算法。
4) 计算:
(8)
这个前向算法需要 次乘法以及 次加法。复杂度为 。
2.3. Viterbi算法
Viterbi算法被研究用来寻找在给定观测序列 最可能的状态序列 ;对于固定的观测序列最大化 就足够了。
定义变量
(9)
完整的Viterbi算法如下:
1) 初始化
(10)
(11)
2) 归纳
(12)
(13)
3) 更新时间
(14)
如果 返回第2步,否则结束算法。
4) 结束
(15)
(16)
5) 路径回读
(17)
当通过Viterbi算法有多条路径产生时,我们选择任意一条或选择最好的 步。
2.4. Baum-Welch算法
为了迭代得出最佳模型 ,我们需要定义一些中间变量。定义 如下:
(18)
这得出的是在给定模型 以及观测序列 时,在时刻 状态为 以及时刻 状态为 的概率。然后定义在给定模型 以及观测序列 时,在时刻 状态为 的概率为 :
(19)
完整Baum-Welch算法的如下:
1) 初始化:随机选择 , , ,得到模型 。
2) 归纳
(20)
(21)
(22)
3) 更新:
(23)
如果 ( 为初定的阈值)返回第2步;否则终止算法;
4) 结束:得出模型的最终参数为 。
3. 实证分析
本章将HMM的思想引入到预测股票的趋势中,然后根据预测指标来构造有效的投资策略。根据股票价格趋势的动量性与持续性,股价走势在一段时间内,涨和跌的股票各自都存在一种明确的模式与其对应,都分别可由一个HMM模型来描述;同时股票的行情数据以及基本面数据表现例如换手率、收益率、股票市值可由有限个服从马尔可夫过程的隐状态所决定,且满足齐次马尔可夫假设和观测独立性假设。因此金融中引入HMM模型是有效的。
3.1. HMM训练过程
通过隐马尔可夫模型来预测个股未来一段时间股价的涨跌。假设对于个股的持仓周期为 天,在交易日 ,通过构造模型去预测 日个股股价相对于时刻 的涨跌。具体步骤如下:
1) 选取数据:假设观测序列长度为 ,那么将每个股票的技术面信息以及基本面信息切分成日频的观测序列,每一日的信息向量作为特征向量对应HMM语音识别模型中的每一个观测值向量,取 到 日的特征向量,获得长度为 的观测序列,对应HMM模型中的每一个观测序列。
2) 训练样本:对数据样本进行上涨与下跌模型样本的分割。在模型训练时,我们选择 日股价相对 日上涨的股票作为上涨模型的训练样本,根据多观测序列的训练算法训练出上涨模型的连续观测序列HMM参数;选择 日股价相对于 日下跌的股票作为下跌模型的训练样本,根据多观测序列的训练算法训练出下跌模型的连续观测序列HMM参数;
3) 模型预测:在进行实际预测时,在 日,我们分别将每个股票在 到 日的信息向量即特征向量作为特征输入训练好的上涨模型和下跌模型中,计算出不同模型下观测到该观测序列的概率p(上涨)与 。如果p(上涨) > p(下跌),则说明该观测序列由上涨模型生成的概率更大,该股票在 日相对于 日上涨的概率大于下跌的概率;反之,则认为该股票下跌的概率大于上涨的概率。
3.2. 策略设计及结果
本文选取了沪深300成分股的日频数据进行建模然后构建量化策略来实证分析。根据影响股票收益率的特征当中从技术面指标中选取的数据包括沪深300成分股的收盘价序列、开盘价序列、最高价序列、最低价序列;同时从基本面指标中选取的数据包括沪深300成分股的日换手率序列、日收盘时的流通市值序列。时间范围为2016.1.1~2018.8.30;
根据个股“上涨”模式与“下跌”模式的概率可以设计个股在模式下的条件概率,即“上涨”条件概率,它的思想是个股在未来一段时间的表明会上涨的概率。所以设计出对应的“上涨”条件因子:HMM = p(上涨) ÷ (p(上涨) + p(下跌));
在沪深300成分股中,基于HMM模型选股策略即“上涨”条件因子策略过程如下:
1) 在调仓日 时,计算出当日沪深300成分股全部个股的“上涨”条件因子;
2) 选股时去除ST、PT股,去除停牌股票,去除上市未满一年股票,去除每股收益小于0股票;
3) 采取行业中性按照行业进行选股,根据“上涨”条件因子数据从大到小排名对成分股进行选取,从而挑选出排名前20%的股票进行投资;
4) 根据成分股的比例计算出每一个行业的占比 ;
5) 行业的股票等资金投入,第 个行业有 只股票投资,则行业的每只个股投入资金比例为 ;
6) 根据资金情况以及个股收盘价计算出调仓日个股买入的仓位数量。
7) 计算日收益率、基准收益率;然后计算年化收益率、最大回撤、夏普比、最长修复时间等指标策略净值图如图1所示。
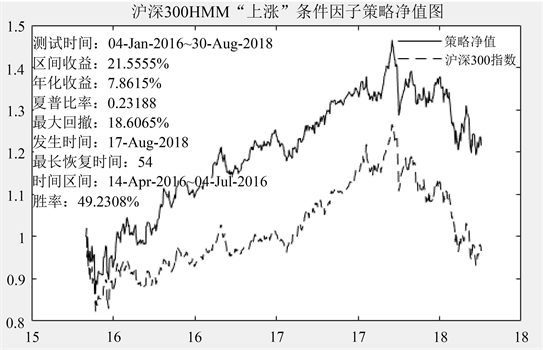
Figure 1. Unhedged net worth chart of stock selection strategy based on HMM model
图1. 基于HMM模型选股策略不对冲净值图
Table 1. The indicator of “Up” conditional factor selection strategy based on HMM model
表1. HMM模型“上涨”条件因子选股策略指标
4. 结论
HMM的思想引入到预测股票的趋势中,根据预测指标来构造一些有效的投资策略。根据股票价格趋势的动量性与持续性,股价走势在一段时间内,涨和跌的股票各自都存在一种明确的模式与其对应,都分别可由一个HMM模型来描述;同时股票的行情数据以及基本面数据表现例如换手率、收益率、股票市值可由有限个服从马尔可夫过程的隐状态所决定,且满足齐次马尔可夫假设和观测独立性假设。根据表1所示,运用HMM模型构造出的“上涨”条件因子进行选股策略中年化收益率为8.94%,最大回撤为8.61%,而指数年化收益为−1.33%,最大回撤为26.43%,策略的夏普比远远大于指数投资的夏普比,效果远远超过指数。用HMM模型进行选股更能促使策略抓住一致性趋势,给策略更好的抓准投资的时机,补充策略的缺陷与单一性。
文章引用
张宇思,梁满发. 基于条件随机场的量化选股模型
Quantitative Stock Picking Model Based on Conditional Random Fields[J]. 统计学与应用, 2019, 08(02): 296-302. https://doi.org/10.12677/SA.2019.82034
参考文献
- 1. 郭平. 贝叶斯概率图像分割中混合模型参数高效计算的研究[J]. 计算机科学, 2002, 29(8): 101-103.
- 2. 郭平, 卢汉清. 贝叶斯概率图像自动分割研究[J]. 光学学报, 2002, 22(12): 1479-1483.
- 3. 郭松涛, 孙强, 等. 基于改进小波域隐马尔可夫模型的遥感图像分割[J]. 电子与信息报, 2005, 27(2): 286-289.
- 4. 林亚忠. 基于Gibbs随机场模型的医学图像分割新算法研究[D]: [博士学位论文]. 广州: 第一军医大学, 2004.
- 5. Zhang, L. and Ji, Q. (2010) Image Segmentation with a Unified Graphical Model. IEEE Transactions on Pattern Analysis and Machine In-telligence, 32, 1406-1425. https://doi.org/10.1109/TPAMI.2009.145
- 6. Zhang, L. and Ji, Q. (2011) A Bayesian Network for Automatic and Interactive Image Segmentation. IEEE Transaction on Image Processing, 20, 2582-2593. https://doi.org/10.1109/TIP.2011.2121080
