Statistics and Application
Vol.
08
No.
05
(
2019
), Article ID:
32732
,
12
pages
10.12677/SA.2019.85093
Research on Internet Credit Risk Prediction Based on Model Fusion
Hongyan Fei, Hao Huang
School of International Technology & Management, University of International Business and Economics, Beijing
Received: Oct. 8th, 2019; accepted: Oct. 22nd, 2019; published: Oct. 29th, 2019

ABSTRACT
The prediction of the credit risk of Internet credit is a key factor for the sustainable development of Internet finance. It can accurately estimate the credit risk of borrowers before lending, effectively reducing the possible risk loss of enterprises. With the development of machine learning, the algorithm model of machine learning has been applied more and more in the credit risk of Internet credit. In order to explore the effect of integrating tree model and linear model in the prediction of credit risk of Internet credit, this paper adopts Stacking model fusion method to design the credit risk prediction model, in which the first layer model is random forest, XGBoost and LightGBM and the second layer model is logistic regression, and conducts experiments on the real data of Clap to Borrow. Compared with the performance of the single model on AUC, accuracy and time consuming, the results show that the fused model, although takes longer time, but performs better in terms of AUC and accuracy, which provides a new idea for the construction of financial credit risk prediction model.
Keywords:Logistic Regression, the Credit risk, Random Forests, XGBoost, LightGBM
基于模型融合的互联网信贷信用风险预测研究
费鸿雁,黄浩
对外经济贸易大学信息学院,北京
收稿日期:2019年10月8日;录用日期:2019年10月22日;发布日期:2019年10月29日

摘 要
互联网信贷信用风险的预测是互联网金融可持续发展的关键因素,在放贷前准确预估借款人的信用风险,能有效较低企业可能的风险损失。随着机器学习的发展,机器学习的算法模型在互联网信贷信用风险方面的应用也越来越多。为了探究树模型和线性模型融合在互联网信贷信用风险预测的效果,本文采用Stacking模型融合方法设计了信用风险预测模型,其中第一层模型为随机森林、XGBoost、LightGBM,第二层模型为逻辑回归。并且在拍拍贷的真实数据上进行实验,对比了融合后的模型和单模型在AUC、准确率和耗时上的表现,结果表明融合后的模型虽然耗时长一些,但是在AUC和准确率方面都比单模型的效果要好,为互联网金融信贷风险预测模型的构建提供了一个新的思路。
关键词 :逻辑回归,信用风险,随机森林,XGBoost模型,LightGBM模型

Copyright © 2019 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
网络借贷是一种新型的互联网金融模式,而在如何快速、准确的综合评估借款人的信用风险则成为了互联网金融能否健康可持续的发展的关键因素,这在工业界备受重视,如今在预测信贷信用风险领域有很多学者进行研究,也取得了不错的进展,但是还有待进一步的深入研究 [1]。
对用户的信用风险的评估本质是上是一个二分类问题,对此主要有三种解决方法:统计分析、定性分析、人工智能方法 [2]。近年来,随着机器学习算法的发展,机器学习在金融信用风险评估领域的应用也越来越广。Malekipirbazari等人提出了一种基于随机森林的借款人信用评估方法,利用借贷平台Lending Club上的真实用户数据进行预测,取得不错的效果 [3]。李昕、戴一成基于BP神经网络构建了信用风险评估模型,实验结果表明BP神经网络具有较高的预测准确率,适合平台和投资者甄选优质借款人 [4]。这些机器学习算法模型的单模型应用已经有了广泛的研究,而模型之间的融合还有进一步探讨的空间。2016年FaceBook提出了GBDT和逻辑回归相融合模型对点击率进行预测,融合后的模型比单模型效果的提升了3% [5]。本文将树模型和线性模型融合的方法引入信用风险评估中,基于拍拍贷的数据建立分类预测模型,为企业和投资者提供决策依据,结果表明树模型和线性模型的融合效果比单模型的效果要好。
2. 模型介绍
2.1. 逻辑回归模型
逻辑回归属于广义线性回归分析模型,在二分类问题中有广泛的应用,通过Logistic函数将目标值Y的取值归一化到0和1之间,使用梯度下降法或拟牛顿法不断的迭代,直到损失函数收敛为止。对于二分类问题,设:
(1)
则似然函数为:
(2)
对数似然函数为:
(3)
其中w是权重向量, 是w和x的内积。对L(w)求极大值,得到w的估计值 [6]。逻辑回归通常采用梯度下降法和拟牛顿法来求解对数似然函数的最优化问题。假设w的极大似然估计值为 ,则逻辑回归模型为:
(4)
(5)
2.2. 随机森林模型
随机森林是Bagging集成学习模型的代表,以决策树为基学习器构建Bagging模型,并且引入特征随机选择的思想,对模型进行训练,输出结果由多棵决策树决定 [7]。随机森林的主要流程是:对每棵树而言,随机有放回的抽取N个样本作为该树的训练集;如果每个样本的特征数量为M,则选择一个m,令 ,每次在M个特征中随机抽取m个特征进行分裂,分裂点是这个m个特征中最优的那个;每棵树都尽可能深的生长,不进行剪枝;对所有决策树的结果进行加总得到输出结果,回归问题使用多数投票方法,回归问题使用取平均值的方法。
2.3. XGBoost模型
XGBoost模型是Chen等人在2016年提出的一种Boosting模型 [8],在传统GBDT算法的基础上,对损失函数进行二阶泰勒展开,并且加入了正则化项,平衡模型的复杂度和的目标函数的下降速度,能够有效解决过拟合问题。Boosting的思想是将多个弱学习分类器集合起来形成一个强学习分类器,而XGBoost所用到的树模型是CART树。XGBoost通过不断的添加树来分裂特征,每添加一棵树就是在学习一个新函数来拟合上个函数的残差。在对数据进行预测时,就是这个数据的每个特征都会落到一个叶子结点上,最后的输出值就是这些树的分数的和。XGBoost的算法模型如公式(6)所示,xi为第i个样本的特征向量,fk是一个回归树,F是回归树的集合。
(6)
目标函数如公式(7)所示,包含了自身的损失函数和政策化惩罚项,其中fi为第i棵树; 表示t棵树模型的组合的预测值。
(7)
XGBoost一次添加一棵树,整个优化流程如下:
(8)
将公式(8)代入公式(7)得公式(9),其中C为常数:
(9)
XGBoost的思想是在 的二阶泰勒展开来求得近似值,引入正则项后,得:
(10)
其中: ,。
2.4. LightGBM模型
LightGBM是由微软亚洲研究院在2017年提出的一种GBDT框架 [5],相较于传统的GBDT算法,LightGBM的优化主要包括三部分:基于Histogram的决策树算法、带有深度限制的Leaf-wise的叶子生长策略、直方图做差加速,既提升了算法的效率,又能防止过拟合。
Histogram算法的基本思想是先把连续的浮点特征值离散化为k个整数,同时构造一个宽度为k的直方图。在遍历数据的时候,根据离散化后的值作为索引在直方图中累计统计量,当遍历一次数据后,直方图累积了需要的统计量,然后根据脂肪乳的离散值,遍历寻找最优的分割点。
在Histogram算法的基础上,LightGBM进行进一步的优化,即带有深度限制的Leaf-wise的叶子生长策略,每次从当前所有叶子结点中,找到分裂增益最大的一个叶子,然后分裂,如此循环。LightGBM的另一个优化是直方图做差加速,一个叶子的直方图可以由它的父节点的直方图和兄弟节点的直方图做差得到,因此直方图做差仅需遍历直方图的k个桶,所以LightGBM可以用非常小的代价得到兄弟叶子的直方图,在速度上可以提升一倍。
3. 实验过程
3.1. 实验数据和描述
本实验所采用数据来自拍拍贷“魔镜杯”风控数据大赛,数据集共有三个数据表,分别是用户行为信息表Master、用户登录数据表LogInfo、用户信息修改数据表Userupdate。用户行为信息表Master有5万多条数据,每个样本包含228个特征;用户登录数据表LogInfo有96万条数据;用户信息修改数据表Userupdate有61万条数据,数据特征已经进行了脱敏处理。三个表的主要特征如表1、表2、表3所示:
Table 1. User behavior information table
表1. 用户行为信息表
Table 2. User login data table
表2. 用户登录数据表
Table 3. User information update table
表3. 用户信息修改数据表
3.2. 数据预处理
1) 数据清洗
数据预清洗主要包括缺失值处理、文本处理、删除常变量。
缺失值处理:用户行为信息表Master的行和列的缺失值有不同处理方式。列(属性)统计缺失值比率,缺失值比率为60%左右的数值型特征用−1填充,将“是否缺失”看做另一种类别。其他缺失值比率比较小的数值型特征用中值填充,字符型特征用unknown填充。行统计每个样本的属性缺失值个数,将缺失值个数按从小到大排序,以序号为横坐标,缺失值个数为纵坐标,画出图1散点图,有部分样本缺失值很高,对缺失值超过120的样本进行删除。

Figure 1. Number of missing value attributes for each sample
图1. 每一条样本缺失值属性个数
文本处理:对用户行为信息表Master中含有空格的文本型特征进行删除空格处理,并统一取值形式(将重庆、重庆市统一为重庆)。对用户信息修改数据表Userupdate中的文本型数值统一大小写。
删除常变量:计算用户行为信息表Master中数值型特征的方差,删除部分方差较小的特征,如表4所示,删除方差小于0.1的特征。
Table 4. Sort of variance
表4. 方差排序
2) 特征工程
特征工程主要包括成交时间离散化、类别特征变换、特征衍生、特征选择。
成交时间离散化:对用户行为信息表Master中的成交时间进行离散化处理。以起始时间为第一周,将日期变量按周离散化。
类别特征变换:统计用户的居住地省份和户籍省份特征的违约率,各取违约率最高的前五名省份进行二值化。之后使用XGBoost挑选重要的特征(图2、图3、图4、图5),将特征重要性排名前三的城市进行二值化。
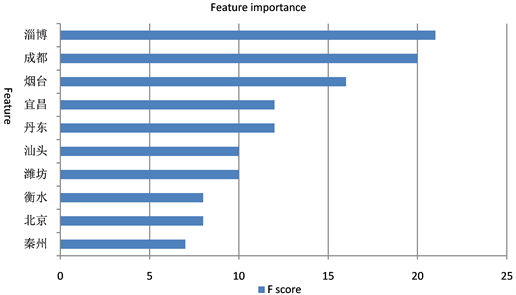
Figure 2. City importance ranking
图2. 城市重要性排名

Figure 3. City importance ranking
图3. 城市重要性排名

Figure 4. City importance ranking
图4. 城市重要性排名

Figure 5. City importance ranking
图5. 城市重要性排名
特征衍生:统计用户登录数据表LogInfo和用户信息修改数据表Userupdate中用户登录次数和用户更新信息的次数,并命名为Log_count和Updat_count加入到用户行为信息数据表Master中,新字段的缺失值由0填补。户籍省份和居住地省份是否一致衍生出一个新特征,由四个城市特征的非重复计数衍生生成登陆IP地址的变更次数。
特征选择:将数据按照7:3划分成训练集和测试集,并利用XGBOOST筛选特征,训练10个模型,并对10个模型输出的特征重要性去平均,最后对特征重要性进行归一化,表5是重要性排名前16的特征(cum_importance:累计重要性;norm_importance:归一化),并删除重要度小于0.01的特征。
Table 5. Feature importance
表5. 特征重要性
3) 样本均衡
在进行模型训练之前要观察一下正负样本的比例,如果样本不均衡时直接使用原样本进行训练,则会使得模型倾向于关注占比高的那一类样本,进而对多数类样本识别率比较高,对少数类样本识别率比较低 [9],所以要进行样本均衡处理。对于不均衡样本,通常有两种方法使得样本均衡,增加正类样本数量的方法被称为过采样,减少负类样本数量的方法被称为欠采样。Chawla等学者提出了SMOTE的方法来解决数据不均衡问题,SMOTE的思想是对少数类样本的K个近邻随机抽取N个值进行随机线性插值,进而构成新的少数类样本 [10]。
本实验样本中正负比例为13:1,使用SMOTE,采取过采样的方法解决类别不平衡问题,平衡后正负样本比例为1:1。
4. 模型训练
4.1. 模型调参与融合
模型的参数对模型的预测结果的影响很大,本实验使用Python的Hyperopt包进行模型调参,Hyperopt通过贝叶斯优化来调整模型的参数,而且相较于基于全局搜索的GridSearch方法而言,Hyperopt速度更快效率更高;Random Search虽然速度比较快,但是可能遗漏空间上一些比较重要的点,Hyperopt则精度更高。而且Hyperopt支持暴力调参、随机调参等策略,也可结合MongoDB进行分布式调参。
模型融合是构建并结合多个学习器来完成学习任务,模型融合的方法主要有Blending和Stacking。Stacking是一种分层模型集成框架。以两层为例,第一层由多个基学习器组成,其输入原始训练集,第二层的模型以第一层基学习器的输出作为特征加入训练集进行再训练,从而得到完整的stacking模型。Blending和Stacking大致相同,但是Blending的主要区别在于训练集不是通过K-Fold的CV策略得到预测值从而生成第二阶段模型的特征,而是将K-Fold CV换成HoldOut CV。但是Blending可能会产生过拟合问题,Stacking使用多次的CV会比较稳健,所以本实验选用Stacking的方法进行模型融合。
海量的离散特征 + 逻辑回归模型,因其较高的精度和较少的运算开销在业界广为使用。但是逻辑回归无法捕捉到非线性特征对标签的影响,因而提升逻辑回归精度的有效方法时构造有效的交叉特征。2014年FaceBook提出了树模型GBDT和逻辑回归的融合模型 [8],利用GBDT构造有效的交叉特征,从根节点到叶子结点的路径代表部分特征组合的一个规则,提升树将连续特征转化为离散特征,明显提升了线型模型的精度。
所以本实验也采用树模型和线性模型相结合的方法进行模型融合。本实验的第一层模型是XGBoost、随机森林和LightGBM,对着三个模型进行调参后找到最优参数值,将其产生的预测值作为新特征,输入第二层模型逻辑回归模型中,进而对数据进行预测。
4.2. 模型评价标准
分类模型常用的评价标准有召回率、精确率、F1分数、准确率、AUC。召回率又被称为查全率,是正确预测的样本中实际为正的样本的占比。精确率又被成为查准率,是预测为正的样本中实际为正的样本占比。召回率和精确率是互相矛盾的,一个取值高,另一个取值则会低,需要根据不同的情况选择使哪个指标更高。F1分数是精确率和召回率的调和,同时兼顾了精确率和召回率,在多分类任务中,F1分数是最常用的指标。准确率表示的正确预测的样本数占总数的比例。AUC是接受者操作特征曲线下的面积,常用来评估二分类模型。
本文主要采用AUC和准确率分数为模型的主要评价标准。相较于召回率、精确率、F1分数、准确率,AUC在二分类任务中应用的更多。因为一般分类模型输出的都是概率,这时就需要设置一个阈值来进行分类,阈值的大小则会对召回率、精确率、F1分数、准确率产生影响,而AUC则没有这个问题。AUC和准确率有时会产生矛盾,这时则优先选择AUC,因为准确率是基于较佳的截断值进行计算的,但是这个较佳的截断值并不是总体分布的最佳截断值,只是某个随机样本的一个属性指标,而AUC基于所有可能的截断值进行计算,所以更稳健 [11]。
5. 实验结果
5.1. 模型调参结果
使用Hyperopt对XGBoost、随机森林、LightGBM三个算法模型分别进行调参,调参前后对比如表6所示,可以发现调参后模型的AUC和准确率值均有所提升。其中随机森林调参后AUC提升,准确率却降低,因AUC相对准确率来说更稳健,所以两者冲突的时候以AUC为准,因此随机森林的性能在调参后是有所提升的。
Table 6. Compare before and after adjusting parameters
表6. 调参前后对比
XGBoost、随机森林、LightGBM三个算法模型的最优参数分别如表7、表8、表9所示:
Table 7. The optimal parameter of XGBoost
表7. XGBoost最优参数
Table 8. The optimal parameter of random forests
表8. 随机森林最优参数
Table 9. The optimal parameter of LightGBM
表9. LightGBM最优参数
5.2. 不同算法模型结果对比分析
本实验对比了XGBoost、随机森林、LightGBM、逻辑回归,以及模型融合的性能,如表10所示:
Table 10. Performance comparison of different models
表10. 不同模型性能对比
由表10可知,四个单模型和融合模型的AUC排名由高到低是融合模型、LightGBM、XGBoost、随机森林、逻辑回归。在模型融合之前,对单模型的调参提升了单模型的AUC,而经过Stacking的融合后,信用风险预测模型的AUC和准确率得到进一步提升,融合后的模型AUC比表现最差的逻辑回归提升了0.0724,准确率提升了0.2187;比表现最好的LightGBM的AUC提升了0.0319,准确率提升了0.0107。
融合后的模型虽然在AUC和准确率上都有所提升,但是确实耗时最长的,耗时43.77,比四个单模型中耗时最长的XGBoost的耗时还要多近一倍的时间。这是因为模型的复杂度越高,耗时也就越长。在本实验中模型融合的耗时还是可以承受的,在实际应用中面对海量信息如果耗时太长则需要权衡一下耗时和预测准确率之间的关系。
6. 总结
本文针对金融领域的信用风险评估问题,建立了信用风险评估模型,以随机森林、XGBoost、LightGBM为第一层模型,逻辑回归为第二层模型,使用Stacking的融合方法进行模型融合。最后结果表明模型融合的效果要优于单模型,但是耗时也更长。本文的创新点之一在于数据预处理方面,本文对原始特征进行挖掘,使得特征和预测目标之间的联系更明显一些,在实际应用中,可以考虑根据现有特征衍生出一些在区分高风险用户方面效果更好的特征;其次是树模型和线性模型的融合,将Bagging类算法的代表——随机森林、Boosting算法的代表——XGBoost、以及XGBoost的改进算法LightGBM和逻辑回归进行了融合,并且最终取得融合效果较好。
基金项目
国家重点研发计划资助(National Key R&D Program of China),项目编号:2017YFB1400700。
文章引用
费鸿雁,黄 浩. 基于模型融合的互联网信贷信用风险预测研究
Research on Internet Credit Risk Prediction Based on Model Fusion[J]. 统计学与应用, 2019, 08(05): 823-834. https://doi.org/10.12677/SA.2019.85093
参考文献
- 1. 于晓虹, 楼文高. 基于随机森林的P2P网贷信用风险评价、预警与实证研究[J]. 金融理论与实践, 2016(2): 53-58.
- 2. Redmond, U. and Cunningham, P. (2013) A Temporal Network Analysis Reveals the Unprofitability of Arbitrage in the Prosper Marketplace. Expert Systems with Applications, 40, 3715-3721. https://doi.org/10.1016/j.eswa.2012.12.077
- 3. Malekipirbazari, M. and Aksakalli, V. (2015) Risk Assessment in Social Lending via Random Forests. Expert Systems with Applications, 42, 4621-4631. https://doi.org/10.1016/j.eswa.2015.02.001
- 4. 李昕, 戴一成. 基于BP神经网络的P2P网贷借款人信用风险评估研究[J]. 武汉金融, 2018(2): 33-37.
- 5. Ke, G.L., Meng, Q., Finley, T., Wang, T.F., Chen, W., Ma, W.D., Ye, Q.W. and Liu, T.-Y. (2017) LightGBM: A Highly Efficient Gradient Boosting Decision Tree. Advances in Neural Information Processing Systems, 30, 3149-3157.
- 6. 李航. 统计学习方法[M]. 北京: 清华大学出版社, 2012: 78-79.
- 7. Verikas, A., Gelzinis, A. and Bacauskiene, M. (2011) Mining Data with Random Forests: A Survey and Results of New Tests. Pattern Recognition, 44, 330-349. https://doi.org/10.1016/j.patcog.2010.08.011
- 8. Chen, T. and Guestrin, C. (2016) XGBoost: A Scalable Tree Boosting System. Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, August 13-17, 2016, 785-794. https://doi.org/10.1145/2939672.2939785
- 9. Sun, Y., Wong, A.K.C. and Kamel, M.S. (2009) Classification of Imbalanced Data: A Review. International Journal of Pattern Recognition and Artificial Intelligence, 23, 687-719. https://doi.org/10.1142/S0218001409007326
- 10. Chawla, N.V., Bowyer, K.W., Hall, L.O., et al. (2002) SMOTE: Synthetic Minority Over-Sampling Technique. Journal of Artificial Intelligence Research, 16, 321-357. https://doi.org/10.1613/jair.953
- 11. Ling, C.X., Huang, J. and Zhang, H. (2003) AUC: A Better Measure than Accuracy in Comparing Learning Algorithms: Advances in Artificial Intelligence. 16th Conference of the Canadian Society for Computational Studies of Intelligence, AI 2003, Halifax, 11-13 June, 2003.
