Advances in Applied Mathematics
Vol.04 No.04(2015), Article ID:16451,10
pages
10.12677/AAM.2015.44049
Research on Fast Algorithms for Scalar Multiplication of Elliptic Curve Cryptography over GF (3n)
Shaofang Shen, Meng Zhou*
School of Mathematics and System Science, LMIB, Beihang University, Beijing
Received: Nov. 9th, 2015; accepted: Nov. 25th, 2015; published: Nov. 30th, 2015
Copyright © 2015 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
In this paper we investigate the fast algorithm of scalar multiplication based on Elliptic Curve Cryptography (ECC) over fields of characteristic three, and make improvements both in underlying operations and upper operations respectively. In the underlying operations, we deduce a formula of calculating 3kP directly under the affine coordinates based upon the idea of recursion, trading inversion for multiplication and trading multiplication for cube, which reduces the inversion to once; in the upper operations, we adopt the sliding window scalar multiplication method, which reduces the length of the non-zero windows and the total computations of 3P effectively.
Keywords:Elliptic Curve Cryptography (ECC), Scalar Multiplication, Recursion, Sliding Window

GF(3n)椭圆曲线密码体制中标量乘快速算法研究
申少芳,周梦*
北京航空航天大学数学与系统科学学院,LMIB,北京

收稿日期:2015年11月9日;录用日期:2015年11月25日;发布日期:2015年11月30日

摘 要
本文研究了特征为3的椭圆曲线密码体制中标量乘的快速算法,并针对底层运算和上层运算分别进行改进。在底层运算中,采用递推归纳、乘法代替求逆、立方代替乘法的思想提出在仿射坐标下直接计算3kP的算法,将求逆运算降至1次;在上层运算中,采用滑动窗口标量乘的方法,既有效减少了非零窗口的长度又减少了算法中3倍点总的运算量。
关键词 :椭圆曲线密码体制,标量乘,递推归纳,滑动窗口

1. 引言
自1985年Neal Koblitz和Victor Miller分别独立提出椭圆曲线密码体制(ECC, Elliptic Curve Cryptography),其安全性和有效实现性就得到了广泛的关注。ECC属于公钥密码体制,它可以提供同RSA密码体制相同的功能。然而它的安全性建立在椭圆曲线离散对数问题(ECDLP)的困难性之上[1] ,目前求解ECDLP最好的算法具有全指数时间复杂度,与RSA相比,ECC具有如下优良性质:
1) ECC安全性高。在同样的攻破时间内,ECC需要的密钥比RSA要短得多,如160 bite的ECC和1024 bite的RSA有相同的安全性;
2) ECC实现性强。密钥短、存储空间占用少、宽带要求低、运算处理时间短等特点均有利于ECC实现;
3) ECC具有多重选择性。在相同基域下,ECC可以通过改变椭圆曲线方程的系数得到不同的加密算法,拥有更多的选择性,而对于给定的素数 或
或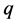 只能对应唯一的一个RSA算法。
只能对应唯一的一个RSA算法。
因此,ECC在信息安全中有广泛的应用。目前, 和
和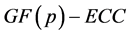 已经研究得比较充分,而对
已经研究得比较充分,而对 的研究工作还很少开展。随着Weil对和Tate对理论的不断进展及基于此而设计的各种安全协议的广泛应用,人们对小素数扩域
的研究工作还很少开展。随着Weil对和Tate对理论的不断进展及基于此而设计的各种安全协议的广泛应用,人们对小素数扩域 的研究产生了浓厚的兴趣。与传统有限域相比,小素数扩域
的研究产生了浓厚的兴趣。与传统有限域相比,小素数扩域 能提供更多、更灵活的密码方案,且针对其的攻击算法相对较少,因此其安全性也比较高。
能提供更多、更灵活的密码方案,且针对其的攻击算法相对较少,因此其安全性也比较高。 作为
作为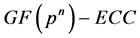 的一种特殊类型,其具有类似于
的一种特殊类型,其具有类似于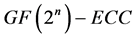 的计算速度快的某些特性,但也有自己的特殊性质,这使得其算术运算效率非常高,极适合作为安全密码算法的载体[2] -[5] 。
的计算速度快的某些特性,但也有自己的特殊性质,这使得其算术运算效率非常高,极适合作为安全密码算法的载体[2] -[5] 。
在ECC中,核心运算就是椭圆曲线的标量乘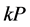 的运算,它是ECC快速实现的关键,而求逆运算又是标量乘中最耗时的,因此采用数学技巧减少求逆次数,对提高运算效率具有重要意义[6] 。
的运算,它是ECC快速实现的关键,而求逆运算又是标量乘中最耗时的,因此采用数学技巧减少求逆次数,对提高运算效率具有重要意义[6] 。
本文首先介绍了ECC的基础知识,包括椭圆曲线的定义及分类以及其上点的运算法则;其次,采用递推归纳、乘法代替求逆、立方代替乘法的思想推导出了仿射坐标系下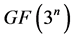 上
上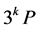 的递推公式;最后基于滑动窗口标量乘对核心标量乘算法进行改进并分析其性能。
的递推公式;最后基于滑动窗口标量乘对核心标量乘算法进行改进并分析其性能。
2. ECC基础知识
2.1. 椭圆曲线的定义及分类
定义1. 设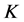 为有限域,
为有限域, 上的Weierstrass方程为
上的Weierstrass方程为
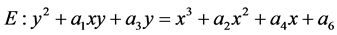 (2.1)
(2.1)
其中,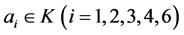 ,称
,称 是域
是域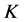 上的椭圆曲线。
上的椭圆曲线。
有限域上椭圆曲线的分类[7] :
(1) 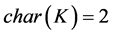
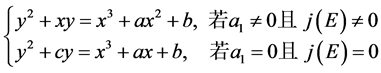 (2.2)
(2.2)
(2) 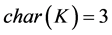
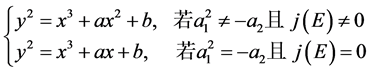 (2.3)
(2.3)
(3) 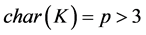
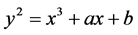 (2.4)
(2.4)
其中 是
是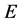 的不变量。
的不变量。
2.2. 椭圆曲线上点的运算法则
定义在域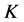 上的椭圆曲线
上的椭圆曲线 的所有点的集合称为
的所有点的集合称为 ,
,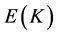 并上一个无穷远点
并上一个无穷远点 构成一个交换群,群上的运算法则由“弦切律”定义。设
构成一个交换群,群上的运算法则由“弦切律”定义。设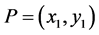 ,
,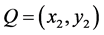 是
是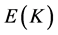 上的任意两个非零点,且
上的任意两个非零点,且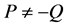 ,下面给出仿射坐标下点加公式
,下面给出仿射坐标下点加公式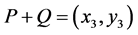 和倍点公式
和倍点公式 :
:
(1) 点加
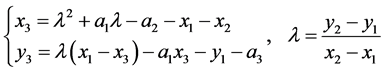
(2) 倍点
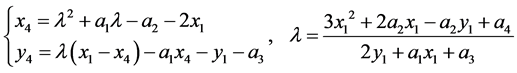
出于安全性考虑,人们通常选择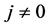 的椭圆曲线来设计椭圆曲线密码系统,故本文我们将对
的椭圆曲线来设计椭圆曲线密码系统,故本文我们将对 时,
时,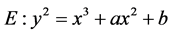 的椭圆曲线进行讨论,其点加和倍点可分别简化为:
的椭圆曲线进行讨论,其点加和倍点可分别简化为:
(1) 点加
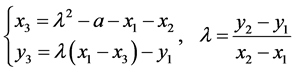 (2.5)
(2.5)
(2) 倍点
 (2.6)
(2.6)
令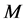 表示域乘法,
表示域乘法,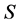 表示域平方,
表示域平方,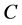 表示域立方,
表示域立方,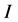 表示域逆,
表示域逆, 表示点加,
表示点加, 表示计算一次域上
表示计算一次域上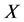 运算所需的时间,
运算所需的时间,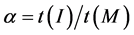 表示逆乘率。与其他运算时间相比,
表示逆乘率。与其他运算时间相比, 可以忽略不计,可知
可以忽略不计,可知 所需的计算复杂度为
所需的计算复杂度为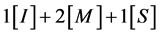 ,
,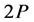 所需的计算复杂度为
所需的计算复杂度为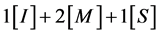 。
。
3. GF(3n)上底层域快速算法综述
标量乘 的运算分为两个层次来完成,一个是底层运算,主要是执行有限域
的运算分为两个层次来完成,一个是底层运算,主要是执行有限域 中各种点加、倍点运算;另一个是上层运算,即椭圆曲线上的点加和倍点运算构成的有限阿贝尔群上的运算。故研究
中各种点加、倍点运算;另一个是上层运算,即椭圆曲线上的点加和倍点运算构成的有限阿贝尔群上的运算。故研究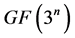 上底层域快速算法应是寻求实现点加、倍点的快速算法。
上底层域快速算法应是寻求实现点加、倍点的快速算法。
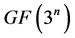 上有限域运算[8] 是其底层运算的基础,设
上有限域运算[8] 是其底层运算的基础,设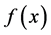 是定义在
是定义在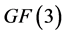 中的
中的 次不可约多项式,则
次不可约多项式,则 可表示为
可表示为
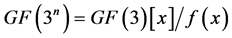
而对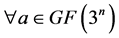 可以唯一地表示为
可以唯一地表示为

又因为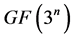 的特征为3,故对
的特征为3,故对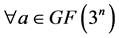 有
有 ,从而对
,从而对 有
有
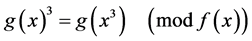
因而元素立方运算比较快,通常比乘法运算或平方运算快至少十倍[8] ,而域逆运算又是最费时的运算,一般而言有
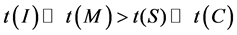
故本文通过引入多个中间变量,多做乘法运算以减少求逆次数,并尽可能将多项式变换成立方项相加减的形式来提高运算速度。
4. GF(3n)上底层域快速算法介绍
4.1. 3P、9P的直接计算公式
为了寻求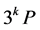 的递推公式,我们先来推导
的递推公式,我们先来推导 、
、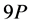 的公式,然后观察、分析,进而推导出直接计算
的公式,然后观察、分析,进而推导出直接计算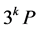 的公式。设椭圆曲线
的公式。设椭圆曲线 ,
,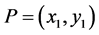 为E上一点,
为E上一点,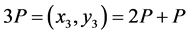 ,先利用式(2.6)得到
,先利用式(2.6)得到 ,再利用式(2.5)得到
,再利用式(2.5)得到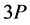 ,即
,即

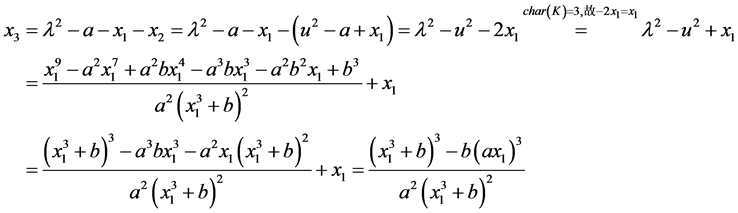
(将分子上的多项式变换成立方项相加减的形式)
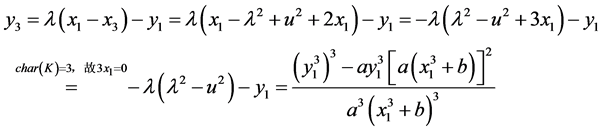
综上所述可得,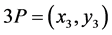 的直接计算公式为
的直接计算公式为
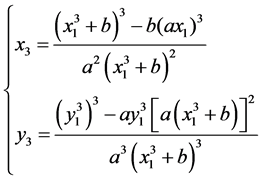 (4.1)
(4.1)
若令
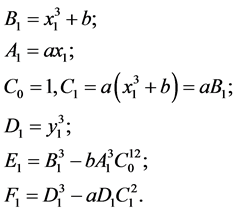
则(4.1)式可化为
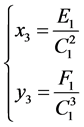 (4.2)
(4.2)
其计算复杂度为 ,相当于不用计算
,相当于不用计算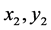 直接得到
直接得到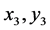 ,而若先得到
,而若先得到 再将其代入(2.5)式得到
再将其代入(2.5)式得到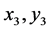 的计算复杂度为
的计算复杂度为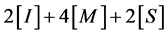 ,相比之下,该算法虽然增加了1次乘法操作和6次立方操作,但却减少了1次求逆运算,不仅在逆乘率较大的情况下极大地减少了运算量,而且为下面推导
,相比之下,该算法虽然增加了1次乘法操作和6次立方操作,但却减少了1次求逆运算,不仅在逆乘率较大的情况下极大地减少了运算量,而且为下面推导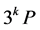 的一般算法提供了便利。
的一般算法提供了便利。
再设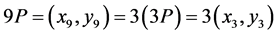 ,将
,将 代入(2.6)式得到
代入(2.6)式得到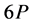 ,再将
,再将 和
和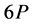 代入(2.5)式得到
代入(2.5)式得到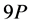 的直接计算公式,结果如下(为书写方便,将
的直接计算公式,结果如下(为书写方便,将 记为
记为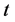 ):
):
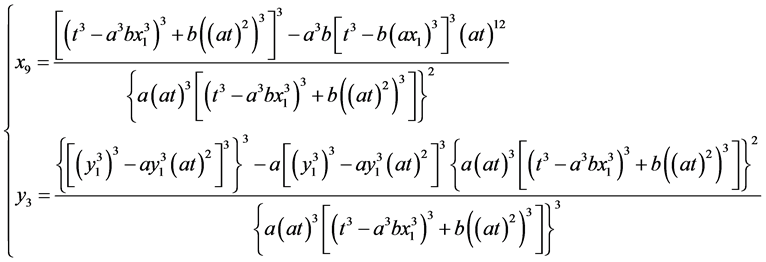 (4.3)
(4.3)
若令
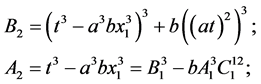
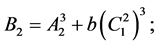
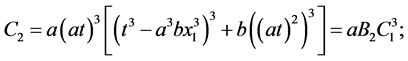
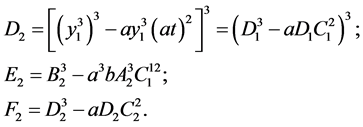
则(4.3)式可化为
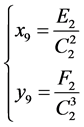 (4.4)
(4.4)
其计算复杂度为 ,与逐次计算的复杂度
,与逐次计算的复杂度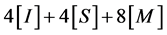 相比,该算法牺牲了12次立方操作,但却减少了3次求逆运算,而
相比,该算法牺牲了12次立方操作,但却减少了3次求逆运算,而 ,可知该算法极大地提高了运算效率。
,可知该算法极大地提高了运算效率。
4.2. 3kP的直接计算公式
根据上一节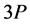 、
、 的计算,以此类推我们可以得到
的计算,以此类推我们可以得到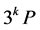 的递推公式。
的递推公式。
设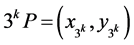 ,令
,令
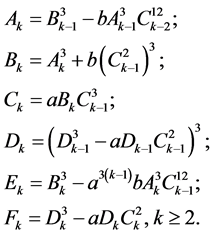
则有
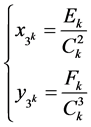 (4.5)
(4.5)
下面给出仿射坐标下直接计算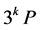 的算法:
的算法:
算法1: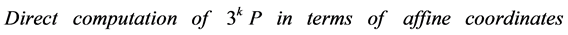
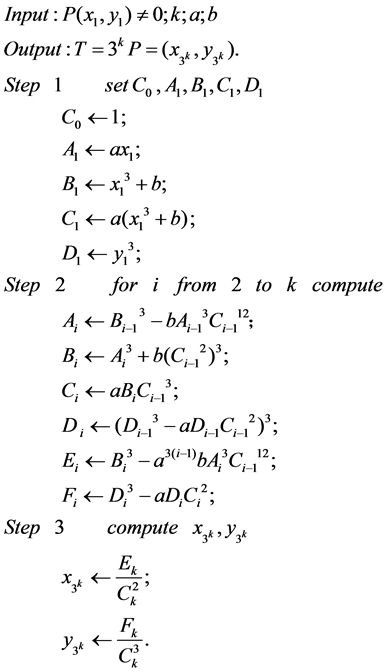
在此递归过程中,先计算当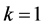 时的
时的 ,其计算复杂度为
,其计算复杂度为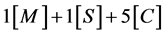 ,此后
,此后 步每次需增加
步每次需增加 ,最后还需计算
,最后还需计算 ,需要
,需要 ,故总的计算复杂度为:
,故总的计算复杂度为:

与此同时,直接计算需要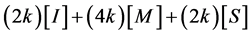 ,虽然增加了
,虽然增加了 ,
, ,但却减少了
,但却减少了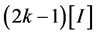 ,当
,当 很大时,直接计算的运算量将会极大地降低。
很大时,直接计算的运算量将会极大地降低。
4.3. 算法性能比较
根据域中运算量的比较,假设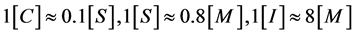 ,如表1。
,如表1。
通过表1,可以直观地看出:直接计算较逐次计算效率有显著的提升,并且随着 值的增大提升幅度也越来越大,特别是当
值的增大提升幅度也越来越大,特别是当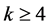 时,提升幅度均可达到
时,提升幅度均可达到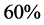 以上。
以上。
5. 基于滑动窗口标量乘算法改进
5.1. 算法介绍
利用底域直接计算 的优势,对传统滑动窗口算法[9] [10] 改进,得到一个新的标量乘法,新算法在赋值阶段比传统算法效率有较大提高。由于新算法预处理栈中存储的都是非零窗口,所以还能抵抗边际信道攻击。
的优势,对传统滑动窗口算法[9] [10] 改进,得到一个新的标量乘法,新算法在赋值阶段比传统算法效率有较大提高。由于新算法预处理栈中存储的都是非零窗口,所以还能抵抗边际信道攻击。
滑动窗口算法分为三个阶段:①标量 编码阶段,计算出
编码阶段,计算出 的
的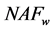 形式,
形式, 为窗口宽度;②预计算
为窗口宽度;②预计算
Table 1. Comparison of different methods in the underlying domain
表1. 不同方法在底层域运算量比较
阶段,计算出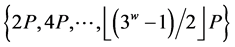 的值存储在一个表中,供下一阶段查询使用;③赋值阶段,利用预计算表计算出
的值存储在一个表中,供下一阶段查询使用;③赋值阶段,利用预计算表计算出 [11] [12] 。
[11] [12] 。
将标量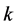 改写成(5.1)式:
改写成(5.1)式:
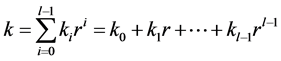 (5.1)
(5.1)
那么计算标量乘 可改写成(5.2)式:
可改写成(5.2)式:
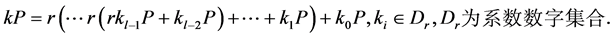 (5.2)
(5.2)
算法2: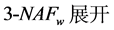
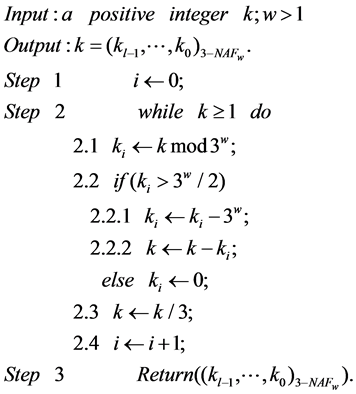
算法3:
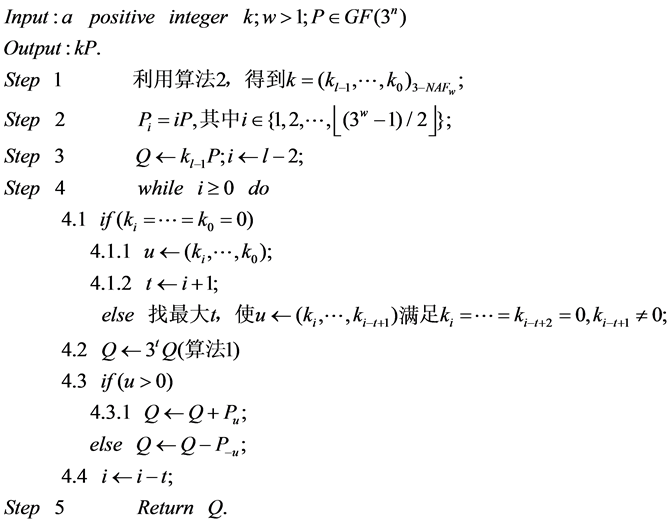
5.2. 算法性能分析与结论
算法2是对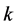 进行重新编码,
进行重新编码, 展开数字集
展开数字集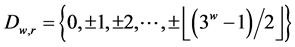 ,且在其展开式中任意
,且在其展开式中任意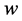 个邻接数字中最多只有1个非零数字[10] ,故任意两个非零数字之间至少有
个邻接数字中最多只有1个非零数字[10] ,故任意两个非零数字之间至少有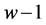 个0,其非零数字密度为
个0,其非零数字密度为 ,算法平均需要
,算法平均需要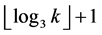 次3倍点和
次3倍点和 次点加。
次点加。
算法3与传统滑动窗口算法的区别在于赋值阶段,对于固定基点的标量乘法,预计算表不需要频繁更换,故建立预计算表在整个标量乘中所占比例不大[9] ,而赋值阶段对于提高标量乘的计算复杂度就显得格外重要。赋值阶段的复杂性与非零窗口的个数 有关,文献[13] 给出非零窗口的密度是
有关,文献[13] 给出非零窗口的密度是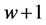 ,而在
,而在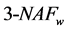 展开式中任意个非零数字之间至少有
展开式中任意个非零数字之间至少有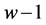 个0,故Step 4最多执行
个0,故Step 4最多执行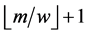 次,每次执行一次
次,每次执行一次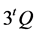 和一次点加,故算法3的计算复杂度为
和一次点加,故算法3的计算复杂度为
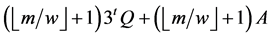 (5.3)
(5.3)
由于滑动窗口可变,因此可以有效地减少非零窗口的长度,从而减少点加运算量;此外,由于在Step 4中采用直接计算 的递归算法,在逆乘率较高时有效地减少了算法中3倍点总的计算量。
的递归算法,在逆乘率较高时有效地减少了算法中3倍点总的计算量。
6. 结束语
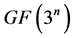 作为
作为 的一种特殊类型,具有其他有限域不可比拟的特点,它可提供更多更加灵活的加密方案且具备较高的安全性。本文采用递归思想,研究了
的一种特殊类型,具有其他有限域不可比拟的特点,它可提供更多更加灵活的加密方案且具备较高的安全性。本文采用递归思想,研究了 椭圆曲线在仿射坐标下直接计算
椭圆曲线在仿射坐标下直接计算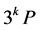 算法,对底层域进行改进,当
算法,对底层域进行改进,当 时,相对于逐次计算而言效率提升到了
时,相对于逐次计算而言效率提升到了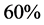 以上;同时采用滑动窗口标量乘的方法对上层域进行改进,既有效减少了非零窗口的长度又减少了算法中3倍点总的运算量。
以上;同时采用滑动窗口标量乘的方法对上层域进行改进,既有效减少了非零窗口的长度又减少了算法中3倍点总的运算量。
基金项目
国家自然科学基金NSFC11271040资助。
文章引用
申少芳,周梦. GF(3n)椭圆曲线密码体制中标量乘快速算法研究
Research on Fast Algorithms for Scalar Multiplication of Elliptic Curve Cryptography over GF (3n)[J]. 应用数学进展, 2015, 04(04): 390-399. http://dx.doi.org/10.12677/AAM.2015.44049
参考文献 (References)
- 1. Koblitz, N. (1987) Elliptic Curve Cryptosystems. Mathematics of Computation, 48, 203-209. http://dx.doi.org/10.1090/S0025-5718-1987-0866109-5
- 2. 汪宏, 李宝, 于伟. 特征3有限域上椭圆曲线Montgomery算法[J]. 通信学报, 2008, 29(10): 25-29.
- 3. Kim, K.H., Kim, S.I. and Choe, J.S. (2007) New Fast Algorithms for Arithmetic on Elliptic Curves over Fields of Characteristic Three. Cryptology ePrint Archive: Report 2007/179. http://eprint.iacr.org/2007/179
- 4. 沈丽敏, 陈恭亮, 游永兴. 特征为3的域上的椭圆曲线点的快速计算[J]. 数学杂志, 2004, 24(5): 557-560.
- 5. 李超. 特征为3的有限域上用于密码体制的椭圆曲线[J]. 通信保密,1994, 58(2): 42-47.
- 6. Kim, K.H. (2007) A Note on Point Multiplication on Supersingular Elliptic Curves over Ternary Fields. Cryptology ePrint Archive: Report 2007/310. http://eprint.iacr.org/2007/310
- 7. Hankerson, D., 等著, 张焕国, 译. 椭圆曲线密码学导论[M]. 北京: 电子工业出版社, 2005.
- 8. Smart, N.P. and Westwood, E.J. (2003) Point Multiplication on Ordinary Elliptic Curves over Fields of Characteristic Three. Applicable Algebra in Engineering, Communication and Computing, 13, 485-497. http://dx.doi.org/10.1007/s00200-002-0114-0
- 9. Al-Daoud, E., Mahmod, R., Rushdan, M. and Kilicman, A. (2002) A New Addition Formula for Elliptic Curves over GF(2n). IEEE Transactions on Computers, 51, 972-975. http://dx.doi.org/10.1109/TC.2002.1024743
- 10. Solinas. J.A. (2000) Efficient Arithmetic on Koblitz Curves. Designs, Codes and Cryptography, 19, 195-249. http://dx.doi.org/10.1023/A:1008306223194
- 11. 侯红祥. 椭圆曲线上快速标量乘的研究[D]: [硕士学位论文]. 扬州: 扬州大学, 2008.
- 12. Takagi, T., Yen, S.M. and Wu, B.C. (2004) Radix-r Non-Adjacent Form. Proceedings of 7th Information Security Conference, ISC 2004, Palo Alto, 27-29 September 2004, 2004, 99-110. http://dx.doi.org/10.1007/978-3-540-30144-8_9
- 13. 刘连浩, 申勇. 椭圆曲线密码体制中标量乘法的快速算法[J]. 计算机应用研究, 2009, 26(3): 1104-1108.
NOTES
*通讯作者。
