Advances in Applied Mathematics
Vol.05 No.03(2016), Article ID:18406,4
pages
10.12677/AAM.2016.53051
Direct Method of Stability of Null Solution for Higher Order Ordinary Differential Equations
Zhixiang Wang, Yuedan Jin, Xiangqing Zhao
Department of Mathematics, Zhejiang Ocean University, Zhoushan Zhejiang

Received: Jul. 27th, 2016; accepted: Aug. 18th, 2016; published: Aug. 25th, 2016
Copyright © 2016 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
“Higher order ordinary differential equations can always be transformed to be first order ordinary differential systems”. By this fact, we proved that higher order ordinary differential equation and first order ordinary differential system transformed from it have the same characteristic roots. Then, by Lyapunov Theorem, we show that the stability of null solution of higher order ordinary differential equation can be determined by its characteristic roots.
Keywords:Higher Order Ordinary Differential Equation, First Order Ordinary Differential System, Stability of Null Solution, Characteristic Roots

高阶线性常微分方程零点稳定性的直接判定法
王芝祥,金月丹,赵向青
浙江海洋大学数学系,浙江 舟山

收稿日期:2016年7月27日;录用日期:2016年8月18日;发布日期:2016年8月25日

摘 要
“高阶线性常微分方程都可以化成一阶线性常微分方程组”。证明了高阶线性常微分方程与由它转化所得的一类特殊的一阶线性常微分方程组有相同的特征值,并据此利用李雅普诺夫定理证明了“高阶线性常微分方程零解的稳定性可以由它的特征值直接决定”。
关键词 :高阶线性常微分方程,一阶线性常微分方程组,零解的稳定性,特征值

1. 引言
一阶线性常微分方程组
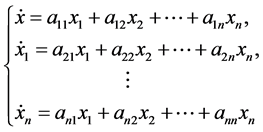 (1.1)
(1.1)
的零解稳定性可以由其系数矩阵 特征值的实部来决定,即李雅普诺夫定理若系数矩阵
特征值的实部来决定,即李雅普诺夫定理若系数矩阵 的特征方程
的特征方程
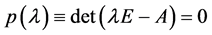
的根(特征根)均具有负实部,则一阶常微分方程组(1.1)的零解是渐近稳定的;若存在特征根具有正的实部,则一阶常微分方程组(1.1)的零解是不稳定的;若特征根非正(零根或具零实部的根),则一阶常微分方程组(1.1)的零解可能是稳定的也可能是不稳定的,具体处决于零根或具零实部的根的重数是否等于1。
毋庸置疑,高阶线性常微分方程
 (1.2)
(1.2)
可以转化为一阶线性常微分方程组,从而利用李雅普诺夫定理可以确定其零解的稳定性,教科书都是这么处理的 [1] - [3] 。然而,这种处理方法往往给初学者一个错觉,即“高阶线性常微分方程零解的稳定性似乎只有转化成一阶线性常微分方程组后通过一阶线性常微分方程组的特征根才可以判定”。实际上,细心的人会发现,往往费尽九牛二虎之力将(1.2)化成一阶线性常微分方程组后计算所得的特征根却与高阶常微分方程(1.2)的特征根是一样的。这种一致性到底是偶然还是必然呢?如果是必然的,那么这种迂回的解法有必要吗?
本文将通过证明高阶线性常微分方程与由它转化所得的一类特殊的一阶线性常微分方程组有相同的特征值,利用李雅普诺夫定理来证明“用高阶常微分方程(1.2)的特征根可以直接判定其零解稳定性”这一事实,从而避免了“高阶常微分方程只能化成一阶常微分方程组来判定零解稳定性”的误解。
2. 高阶方程与一阶线性方程组
引理2.1. 任意高阶线性常微分方程(1.2),都可以化成一阶线性方程组:
 (2.1)
(2.1)
证明:实际上,只要在方程(1.2)中令 即可。抑或参考 [1] [2] 。
即可。抑或参考 [1] [2] 。
引理2.2. 高阶线性常微分方程(1.2)和一阶线性常微分方程组(2.1)有相同的特征根。
证明:一方面, 有特征方程
有特征方程
 (2.2)
(2.2)
另一方面,一阶线性常微分方程组(2.1)的特征方程

故高阶线性常微分方程(2.1)与一阶线性常微分方程组(2.2)有相同特征根。
3. 高阶线性常微分方程零解稳定性直接判定法
由上述命题发现,高阶线性常微分方程零解稳定性的判定可以不用转化为方程组来处理,而是直接用方程的特征根来判定。从而得到:
定理3.1. 若高阶线性常微分方程(1.2)的特征方程
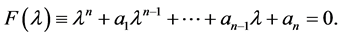
的根(特征根)均具有负实部,则高阶线性常微分方程(1.2)的零解是渐近稳定的;若存在特征根具有正的实部,则高阶线性常微分方程(1.2)的零解是不稳定的;若特征根的实部非正(零根或具零实部的根),则高阶线性常微分方程(1.2)的零解可能是稳定的也可能是不稳定的,具体处决于零根或具零实部的根的重数是否等于1。
证明:根据引理2.1,我们总可以将高阶线性方程(1.2)化成一阶线性方程组(2.1);李雅普诺夫稳定性理论告诉我们线性微分方程组的稳定性由其特征根实部的正负性决定;根据引理2.2,高阶线性方程(1.2)和一阶线性方程组(2.1)有相同的特征根。综上可知,高阶线性方程(1.2)零解的稳定性可以由其特征根决定。
例1 分析下列方程零解的稳定性:
1) 
2) 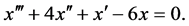
解:1) 二阶线性微分方程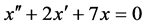 的特征方程为
的特征方程为
 (3.3)
(3.3)
求得特征根

因为特征根的实部均为负,故由定理1得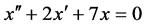 的零解是渐近稳定的。
的零解是渐近稳定的。
2) 三阶线性常微分方程 的特征方程为
的特征方程为
 (3.4)
(3.4)
求得其特征根

因为存在实部大于零的特征根,由定理1可知 的零解是不稳定的。
的零解是不稳定的。
注1. 例1的1)和2)转化为一阶线性常微分方程组后的矩阵分别是

他们的特征方程分别是
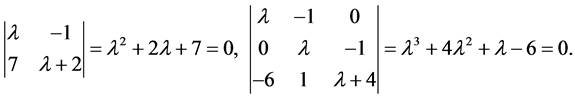
他们与(3.3)和(3.4)相同,用定理1处理高阶线性方程的优势体现得非常明显。
注2. 只有少数一阶线性常微分方程组可以转化为高阶线性常微分方程,所以将一阶线性常微分方程组转化为高阶线性常微分方程来判定其稳定性不仅是复杂的,也不一定是可行的。
基金项目
本文第二作者受到浙江省大学生科技创新活动计划暨新苗人才计划(编号2016R411041)资助。
文章引用
王芝祥,金月丹,赵向青. 高阶线性常微分方程零点稳定性的直接判定法
Direct Method of Stability of Null Solution for Higher Order Ordinary Differential Equations[J]. 应用数学进展, 2016, 05(03): 412-415. http://dx.doi.org/10.12677/AAM.2016.53051
参考文献 (References)
- 1. 王高雄, 朱之铭, 周思铭, 等. 常微分方程(第三版) [M]. 北京: 高等教育出版社, 2010.
- 2. 丁同仁, 李承治. 微分方程教程[M]. 北京: 高等教育出版社, 2002.
- 3. Perko, L. (2001) Differential Questions and Dynamical Systems. 3rd Edition, Sprin-ger-Verlag, Berlin Heidelberg. http://dx.doi.org/10.1007/978-1-4613-0003-8