Advances in Applied Mathematics
Vol.05 No.04(2016), Article ID:19033,5
pages
10.12677/AAM.2016.54077
Research on Posedness of Binary Graded Interpolation
Xiaoqian Fan, Ying Liu, Lihong Cui
Liaoning Normal University, Dalian Liaoning

Received: Nov. 4th, 2016; accepted: Nov. 19th, 2016; published: Nov. 24th, 2016
Copyright © 2016 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
The paper studies from the posedness of bivariate polynomial interpolation. Based on the methods of “adding a horizontal line” and “adding vertical line” in constructing well-posed node group of binary interpolation, this paper further researches and discusses the posedness of binary graded interpolation, and gives geometrical structure and basic characteristics of well-posed node group of binary graded interpolation, then constructs the method that adds parabola for the well-posed node group of binary graded interpolation and generalizes the existing research results. Finally, the numerical examples are given to verify the research results.
Keywords:Well-Posed Node Group, Binary Graded Interpolation, Algebraic Curve

二元分次插值适定性问题研究
范晓倩,刘莹,崔利宏
辽宁师范大学,辽宁 大连

收稿日期:2016年11月4日;录用日期:2016年11月19日;发布日期:2016年11月24日

摘 要
本文从研究二元多项式插值的适定性问题着手,在构造二元分次插值适定结点组的“添加横直线法”和“添加竖直线法”的基础上,对二元分次插值适定性问题进一步研究和探讨,给出了二元分次插值适定结点组的几何结构和基本特征,构造了二元分次插值适定结点组的“添加抛物线”方法,推广了已有的研究结果,最后给出算例对所得研究结果进行了验证。
关键词 :适定结点组,二元分次插值,代数曲线

1. 前言
多元多项式插值是计算数学的一个重要研究课题,也是继一元多项式插值之后的核心研究领域,二元分次插值在数学基本理论研究以及相关学科领域中有重要的地位和作用。而进行多元分次插值时必须解决的问题就是插值的适定性问题或者说是插值多项式函数的唯一存在性问题。梁学章在文献 [1] 中给出了构造二元分次插值适定结点组的“添加横直线法”及“添加竖直线法”,本文在以往学者对二元分次插值研究的基础上 [2] [3] [4] [5] ,进一步研究了二元分次插值适定结点组的基本结构和几何特征,得到了构造二元分次插值适定结点组的“添加抛物线法”,并通过具体例子加以拟合,运用MATLAB软件编程,画出图像,以便观察插值的效果。
2. 基本概念和定理
设 为非负整数,并且
为非负整数,并且 ,
, 代表所有全次数不超过
代表所有全次数不超过 的二元实系数多项式空间,即
的二元实系数多项式空间,即 [1] 。
[1] 。
定义1.1 [1] 设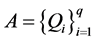 是
是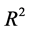 中的
中的 个相异点,对于一个给定的实数组
个相异点,对于一个给定的实数组 ,找一个多项式
,找一个多项式 ,满足如下插值条件
,满足如下插值条件
 (2.1)
(2.1)
如果对于每一个任意给定的实数组 ,方程组(1.1)总存在并且唯一存在一组解,则称该插值问题是适定插值问题,并称这个插值结点组
,方程组(1.1)总存在并且唯一存在一组解,则称该插值问题是适定插值问题,并称这个插值结点组 为关于多项式空间
为关于多项式空间 的一个适定结点组。
的一个适定结点组。
设 为非负整数并且
为非负整数并且 ,
, 表示所有关于
表示所有关于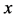 次数不超过
次数不超过 ,关于
,关于 次数不超过
次数不超过 的二元多项式
的二元多项式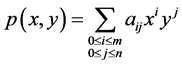 构成的空间。
构成的空间。
定义1.2 设 是
是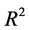 上关于插值空间
上关于插值空间 的
的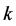 个互异点,对于一个任意给定的实数组
个互异点,对于一个任意给定的实数组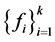 ,找一个多项式
,找一个多项式 ,满足如下插值条件
,满足如下插值条件
 (2.2)
(2.2)
则这个插值问题称为二元分次插值问题。满足条件(1.2)的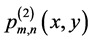 称为该插值问题的插值多项式。
称为该插值问题的插值多项式。
如果对于每一个任意给定的实数组 ,方程组(1.2)总存在的而且是唯一存在的一组解,则称该插值问题是适定插值问题,并称这组插值结点组
,方程组(1.2)总存在的而且是唯一存在的一组解,则称该插值问题是适定插值问题,并称这组插值结点组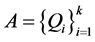 为关于多元分次插值空间
为关于多元分次插值空间 的一个插值适定结点组。
的一个插值适定结点组。
定理1.1 [2] :设 是
是 上关于插值空间
上关于插值空间 的适定结点组。若它的每个点都不在竖直线
的适定结点组。若它的每个点都不在竖直线 上,则在竖直线上任取的
上,则在竖直线上任取的 个互不相同的点与
个互不相同的点与 一起必定构成
一起必定构成 的适定结点组。同样地,若
的适定结点组。同样地,若 的每个点都不在横直线
的每个点都不在横直线 上,则在横直线上任取的
上,则在横直线上任取的 个互不相同的点与
个互不相同的点与 一起必定构成
一起必定构成 的适定结点组。
的适定结点组。
引理1.1 [2] (Bezout)若 次代数曲线
次代数曲线 和
和 次代数曲线
次代数曲线 的交点超过
的交点超过 个,则必有次数既不超过
个,则必有次数既不超过 也不超过
也不超过 的非零多项式
的非零多项式 存在,使得
存在,使得


其中 分别为次数小于
分别为次数小于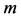 和
和 的二元实系数多项式。
的二元实系数多项式。
基本引理1.2 [2] : 是
是 的适定结点组的充要条件是
的适定结点组的充要条件是 不落在
不落在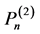 中的任何一条代数曲线上。
中的任何一条代数曲线上。
3. 主要定理及证明
定理2.1: 是
是 上关于插值空间
上关于插值空间 的插值适定结点组,若它的每一个点都不在曲线
的插值适定结点组,若它的每一个点都不在曲线 上,则在该曲线上任取的
上,则在该曲线上任取的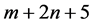 个互不相同的点与
个互不相同的点与 一起必定构成空间
一起必定构成空间 的插值适定结点组。
的插值适定结点组。
定理2.1证明:用 表示
表示 上所取的
上所取的 个点做成的集合,
个点做成的集合, ,则
,则 所含点数为
所含点数为 ,这恰好等于空间
,这恰好等于空间 的维数。下面用反证法证明
的维数。下面用反证法证明 是
是 的插值适定结点组.假设
的插值适定结点组.假设 不是
不是 的插值适定结点组,则由基本引理,必有非零多项式
的插值适定结点组,则由基本引理,必有非零多项式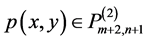 ,
, ,
, 。特别
。特别 ,
, 。由于
。由于 是
是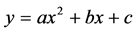 上所取的
上所取的 个不同的点。故
个不同的点。故 有
有 个互不相同的根,由于
个互不相同的根,由于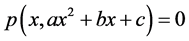 的次数
的次数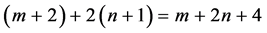 总小于
总小于 ,故
,故 .这说明
.这说明 次数曲线
次数曲线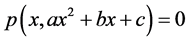 与2次曲线
与2次曲线 有无穷多个交点,由Bezout定理,必有次数小于
有无穷多个交点,由Bezout定理,必有次数小于 的多项式
的多项式 ,使得
,使得 。由于
。由于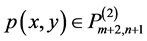 ,故
,故 。又由于在点组
。又由于在点组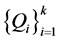 上
上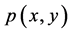 取零值,故有
取零值,故有 ,
,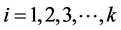 ,从而
,从而 ,
, 。这与
。这与 矛盾,因此
矛盾,因此 是
是 的插值适定结点组。
的插值适定结点组。
4. 具体构造方法及实验示例
下面我们给出构造 中适定结点组的迭加构造方法的流程。
中适定结点组的迭加构造方法的流程。
由于在 上任取一点都可以做成
上任取一点都可以做成 的适定结点组,从它出发,反复应用定理,便可构造出
的适定结点组,从它出发,反复应用定理,便可构造出 的适定结点组
的适定结点组 。在这里我们给出
。在这里我们给出 的适定结点组的构造方法。
的适定结点组的构造方法。
a. 若 。
。
第0步,在 上任取点
上任取点 作为结点,
作为结点, 。
。
第1步,在 上任做一条抛物线
上任做一条抛物线 不通过
不通过 点,在其上任选5个互不相同的点作为新增加的结点。
点,在其上任选5个互不相同的点作为新增加的结点。
……
第 步,在
步,在 上任做一条抛物线
上任做一条抛物线 不通过前面已选好的点,在其上任选
不通过前面已选好的点,在其上任选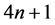 个互不相同的点作为新增加的结点。
个互不相同的点作为新增加的结点。
在前 步取好的
步取好的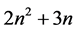 个点构成
个点构成 的适定结点组。
的适定结点组。
b. 若 ,则先用(a)方法,再用梁学章老师提到的定理1.1方法构造。
,则先用(a)方法,再用梁学章老师提到的定理1.1方法构造。
例:设 为
为 上一点,则
上一点,则 ,不经过
,不经过 在斜直线
在斜直线 上任取5个点
上任取5个点 ,
, ,
,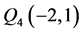 ,
, ,
,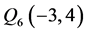 ,则由上述流程知
,则由上述流程知 这六个点构成空间
这六个点构成空间 的插值适定结点组。
的插值适定结点组。
设被插值函数为 ,所确定的唯一的一条插值曲线为
,所确定的唯一的一条插值曲线为

由MATLAB做出被插值函数 和插值函数
和插值函数 的图像见图1。
的图像见图1。
本文研究的“添加抛物线法”比构造二元分次插值适定结点组的“添加横直线法”和“添加竖直线法”复杂,但若空间维数较大,则本文找适定结点组的方法比梁老师的方法要快些。

Figure 1. The effect picture of binary graded interpolation
图1. 二元一次分次插值效果图
致谢
在论文完成之际,我要特别感谢我的指导老师崔利宏老师的热情关怀和悉心指导。在我撰写论文的过程中,崔老师倾注了大量的心血和汗水,无论是在论文的选题、构思和资料的收集方面,还是在论文的研究方法以及成文定稿方面,我都得到了崔老师悉心细致的教诲和无私的帮助,特别是他广博的学识、深厚的学术素养、严谨的治学精神和一丝不苟的工作作风使我终生受益,在此表示真诚地感谢和深深的谢意。在论文的写作过程中,也得到了许多同学的宝贵建议,同时还到许多在工作过程中许多同事的支持和帮助,在此一并致以诚挚的谢意。感谢辽宁省科研基金项目的资助,感谢所有关心、支持、帮助过我的良师益友。最后,向在百忙中抽出时间对本文进行评审并提出宝贵意见的各位专家表示衷心地感谢!
基金项目
辽宁省大学生实践基地建设项目基金资助。
文章引用
范晓倩,刘莹,崔利宏. 二元分次插值适定性问题研究
Research on Posedness of Binary Graded Interpolation[J]. 应用数学进展, 2016, 05(04): 657-661. http://dx.doi.org/10.12677/AAM.2016.54077
参考文献 (References)