Advances in Applied Mathematics
Vol.06 No.07(2017), Article ID:22553,9
pages
10.12677/AAM.2017.67108
An Asset Pricing Model with Memory Coefficient
Xuxia Li
College of Mathematics and Systems Science, Xinjiang University, Urumqi Xinjiang
Received: Oct. 9th, 2017; accepted: Oct. 23rd, 2017; published: Oct. 31st, 2017

ABSTRACT
This paper develops heterogeneous beliefs of the asset pricing model with the evolution fitness in the case of the two types of agents. Introducing memory coefficient, the memory parameter in deviation between the fundamentalists market fraction and chartists market fraction, we develop an asset pricing model with heterogeneous beliefs. By using the theory of difference equation, we discuss about the system of the model for local stability bifurcation analysis, and obtain the effect of main parameters on the stability of the model.
Keywords:Heterogeneous Belief, Memory Parameter, Stability
含记忆系数的资本资产定价模型
李绪霞
新疆大学,数学与系统科学学院,新疆 乌鲁木齐
收稿日期:2017年10月9日;录用日期:2017年10月23日;发布日期:2017年10月31日

摘 要
本文扩展了异质信念下的含基本面分析者和图表分析者两类投资者的资产价格动态模型。引入记忆参数、市场分数差的记忆系数,由此构建了一个资产定价模型。利用差分方程相关理论讨论了其确定性模型的平衡解的存在性和稳定性。其次分析记忆系数的一些性质及其对稳定性区域的影响。
关键词 :异质信念,记忆参数,稳定性

Copyright © 2017 by author and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
在异质信念的资产定价模型中,非理性交易者会在进化的竞争市场中生存,这与Friedman (1953) [1] 中提出的认为非理性交易者将从套利市场中被驱逐出去相矛盾。在大多数异质代理者资产定价模型中,由于短期赢利能力驱动进化选择,非理性交易者可以幸存。与进化适应度有关的记忆长度、长期赢利能力等是国内外读者感兴趣的。Lebaron (2001, 2002) [2] [3] 发现,在金融市场中,若有更多的代理者有长记忆性时,资产价格会产生微小波动,即长期投资者使得市场更加稳定,短期投资者使得市场价格剧烈波动且阻碍资产价格收敛到其基本价值。Hommes and Tatiana Kiseleva (2012) [4] 研究了含有常数的记忆参数对价格动态的影响,讨论了累积效用
和归一化效用
两种特殊类型,发现在累积效用中,随着选择强度变大,分支路径变成了复杂的动态,而且注意到,在含有记忆的效用测量中,在价格序列中暂时的泡沫和崩溃发生不太频繁,但是当它们发生时,价格与基本价格的偏差变得更大,持续时间更长。
因此,本文在Beum-Jo Park(2014) [5] (以下简称BP)的基础上,在市场中同样考虑两类投资者:基本面分析者和图表分析者,对两类投资者引入记忆参数
和市场分数差的记忆系数
。
2. 含记忆系数的动态模型
BP文献中建立的动态模型如下:
(1.1)
其中
代表t时风险资产价格与基础价格的偏差,
,
为无风险资产的收益率,k表示图表分析者的外推系数,
为t时两类交易者市场分数之差,
表示市场中交易者的选择强度,
为基本面分析者的风险厌恶系数,
为t时图表分析者的风险厌恶系数,c为基本面分析者的交易成本。
本文在BP的基础上扩展,假定市场中有两类投资者:基本面分析者和图表分析者,分别用F,C表示。仍然考虑市场中只有一只风险资产和一只无风险资产。
2.1. 记忆系数的引入
BP主要考虑
,
,这里
表示t时h类投资者的净收益,
,
是鞅差序列,令
,
为t − 1时h类投资者对风险资产的需求,
为进化适应度函数。本文在此基础上引入记忆参数
,
,则基本面分析者和图表分析者的进化适应度函数为:
(1.2)
,
为记忆参数,
衡量t − 1时h类投资者的净收益对t时的适应度函数的影响程度,
衡量t − 1时h类投资者的进化适应度函数对t时的适应度函数的影响程度。当
时即为BP的情形。
同时,本文引入两类投资者市场分数差的记忆参数
,则
, (1.3)
记忆系数
是实数。
2.2. 于是我们得到如下的非线性动态系统
(1.4)
通过增维降阶,动力系统变为
(1.5)
3. 确定性系统分析
令
,模型的确定性系统为:
,即
,
,
,
,
,
.
为其平衡解,满足
,即为以下等式:
(2.1)
定理1 (平衡解的存在性):
令
,
,
,
,
为下式的解(若存在)
(2.2)
1、当
时,
为唯一的平衡解,
;
2、当
时,
(1) 若
时,存在平衡解
,
;
(2) 若
时,存在平衡解
,
;
3、当
时,
(1)
时,
是唯一的平衡解;
(2)
时,若
,则存在平衡解
;若
,则存在平衡解
。
证明:由(2.1)第一式可知
恒成立,当
时,可解得
,
。
1、
时,
,则
,又由(2.1)第7式可知
,但是
,两者相矛盾,故此时只有平衡解
。
2、
时,
且
,因此(2.2)式存在两个平衡解
,有(2.1)第7式可知
,
(1) 若
时,
,所以
,则存在平衡解
;
(2) 若
时,
,所以
,则存在平衡解
;
3、
时,
,
(1)
时,方程(2.2)无解,故只有平衡解
;
(2)
时,方程(2.2)有解,又由(2.1)第7式得
,若
,
,则存在平衡解
;若
,
,所以
,则存在平衡解
。
定理2 (稳定性)
1、
,
,
时,基本平衡解
是渐近稳定的;
2、
,或
或
或
时,基本平衡解
不稳定;
3、
且
,
时,
若
,
时,基本平衡解
是渐近稳定的;
4、当
,
时,出现音叉分支,当
时,基本平衡解
稳定,当
时,基本平衡解
不稳定,
。
证明:由定理1,
是系统的基本平衡解,则在
处:
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
.
其中
,
则在
处的Jacobi矩阵为
,
则
故
,
,
,
,
,
1、因为
,所以当
时,
,
时,
,
时,
,
时,
,故基本平衡解
是渐近稳定的;
2、
时,
或
时,
,
时,
,
时,
,
故基本平衡解
是不稳定的;
3、
,
时方程(2.2)无解,若
,则
,且
,
,
时,
,
,
,所以基本平衡解
是渐近稳定的;
4、
,
时,此时特征根都为非负实数,有且仅有可能出现pitchfork分支,即
,解得
,故当
时,基本平衡解
稳定,当
时,基本平衡解
不稳定。
在下面的模拟中参数取值如下
,
,
,
,
,
,
,
,
,
,
.
下面研究选择强度β对确定性系统的敏感性,图1表示选择强度β的音叉分支图,如图所示,基本平衡解保持在确定的选择强度
下,当选择强度超过这个临界值时,基本平衡解变的不稳定,引起了混乱的价格波动,这与定理2的结论相一致。
图2画了
平面的吸引子,在第一个图中,当记忆参数γ由大变小时,价格和时变的风险厌恶系数波动显著,在第二个图中,对于η,当η由小变大时,价格和时变的风险厌恶系数波动小,这说明代理者考虑对实现利润
的权重变大时,预测未来的价格波动变小,而对于上一期的效用函数
的权重变小时,价格波动感小。
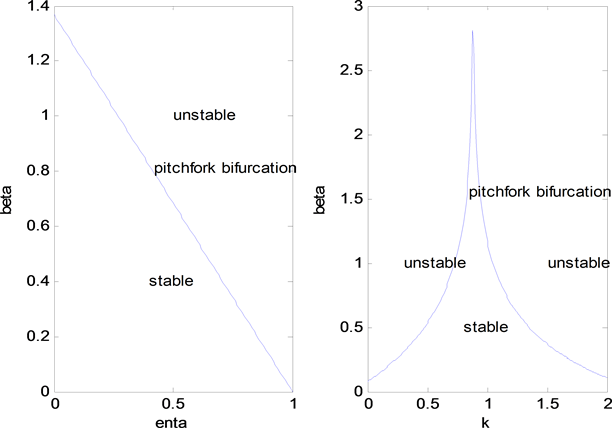
如图3第一个图所示当η变大,即对过去效用函数的记忆权重变大,则β变小,即分支出现的越迟,
故记忆参数η不利于稳定市场。如第二个图所示,图表分析者的趋势推断k,刚开始记忆参数k变大,β变大,当k超过确定的临界值
时,随着k的变大,β变小,即当
时,k变大具有稳定市场的作用,当
时,k的变大使得分支出现的越早,不利于稳定市场。
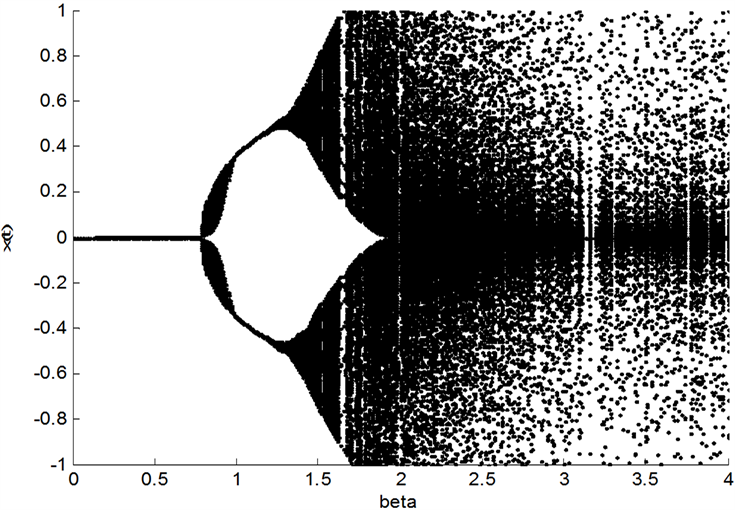
Figure 1. The sensitivity of β to deterministic systems
图1. β对确定性系统的敏感性
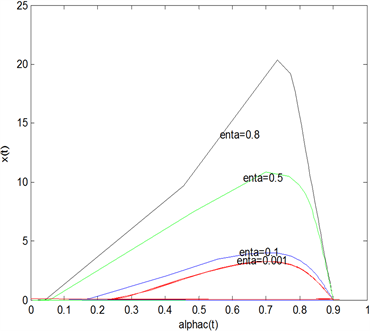
Figure 2.
plane by the change of γ and η
图2. 由γ和η的变化画
平面
图3. n和k对β
4. 总结
本文在BP模型的基础上,加入了记忆参数、记忆系数,建立了含记忆参数的简单的资本资产定价模型,讨论了资本资产定价模型的平衡解及其稳定性、稳定区域及参数对稳定区域的影响。结果显示模型能很好地描述真实市场。
文章引用
李绪霞. 含记忆系数的资本资产定价模型
An Asset Pricing Model with Memory Coefficient[J]. 应用数学进展, 2017, 06(07): 896-904. http://dx.doi.org/10.12677/AAM.2017.67108
参考文献 (References)
- 1. Friedman, M. (1953) The Case of Flexible Exchange Rates. In: Essays in Positive Economics, University of Chicago Press, Chica-go.
- 2. LeBaron, B. (2001) Evolution and Time Horizons in an Agent-Based Stock Market. Macroeconomic Dynamics, 5, 225-254. https://doi.org/10.1017/S1365100501019058
- 3. LeBaron, B. (2002) Short-Memory Traders and Their Impact on Group Learning in Financial Markets. Proceedings of the National Academy of Sciences of the United States of America, 99, 7201-7206. https://doi.org/10.1073/pnas.072079699
- 4. Hommes, C., Kiseleva, T., et al. (2012) Is More Memory in Evolutionary Selection (De)Stabilizing? Macroeconomic Dynamics, 16, 335-357. https://doi.org/10.1017/S136510051000060X
- 5. Beum-Jo, P. (2014) Heterogeneous Risk Aversion and Dynamics of Asset Prices among Bounded Rational Agents. Journal of Banking & Finance, 43, 150-159.