Advances in Applied Mathematics
Vol.06 No.08(2017), Article ID:22854,8
pages
10.12677/AAM.2017.68121
On Tensor Gaussian Distributions
Lingling He, Zerong Lin, Tian Wu, Changqing Xu*
School of Mathematics and Physics, Suzhou University of Science and Technology, Suzhou Jiangsu
*通讯作者。

Received: Nov. 9th, 2017; accepted: Nov. 22nd, 2017; published: Nov. 29th, 2017

ABSTRACT
In this paper, we first introduce the multivariate Gaussian distributions, including the Gaussian distribution of a random vector and the Gaussian distribution of a random matrix. Some basic properties of those Gaussian distributions are also investigated. We then introduce the tensor Gaussian distribution of a random matrix, and present some basic properties for tensor Gaussian distribution.
Keywords:Tensor Gaussian Distribution, Characteristic Function, Matrix Gaussian Distribution
随机张量的高斯分布
何玲玲,林泽榕,吴田,徐常青*
苏州科技大学数理学院,江苏 苏州

收稿日期:2017年11月9日;录用日期:2017年11月22日;发布日期:2017年11月29日

摘 要
本文首先介绍一般多元高斯分布,包括随机向量高斯分布和随机矩阵高斯分布,研究了其基本性质,重点引进随机张量高斯分布,并研究了随机张量高斯分布的基本性质。
关键词 :张量高斯分布,特征函数,矩阵高斯分布

Copyright © 2017 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 背景知识
1.1. 高斯分布的背景知识
正态分布由德国数学家和天文学家Moivre于1733年提出,因德国数学家高斯率先将其应用于天文学研究,故又称高斯分布 [1] 。德国印有高斯头像的10马克钞票上还印有正态分布密度曲线。在高斯对数学各分支的诸多贡献中,对人类文明影响最大的当属高斯分布理论。1812年,法国数学家拉普拉斯指出一个二项分布可用正态分布逼近,并将高斯分布与中心极限定理联系起来。1837年,海根正式系统的提出高斯分布理论。
高斯分布大量的运用于统计学 [2] [3] 、经济学 [4] 、自然科学和社会科学 [5] 中,并用于自然界和人类社会中出现的各类分布的近似。如一类人群的身高、动植物生长发育在不同时期的体重、一个较大群体中个体的智力、记忆力和阅读技巧、工资收入分布、一个有1000多人构成的一个同一年级学生的考试成绩分布等,都服从高斯分布;在诸如航天科学 [6] 、天文与地理 [7] 、光学和量子力学 [8] 等高尖端领域,同样涉及到高斯分布。
一个服从高斯分布的一元随机变量
对应的高斯分布密度函数(PDF)完全由其均值(
)和方差(
)唯一确定。若随机变量
服从均值为
、方差为
的正态分布,那么x的概率分布密度函数(PDF)为
(1.1)
记为
。若
,则称x服从标准正态分布,记为
。
为了得到随机向量的高斯分布,我们令
,其中
独立同分布(i.i.d)由独立性我们可以得到
的密度函数为
(1.2)
记为
,并称
服从标准正态分布。为了得到随机向量的更一般的高斯分布,我们记随机向量
的均值为
,且记x的协方差矩阵
(正定或半正定矩阵)的一个满秩分解为
(1.3)
若
与
具有相同分布且
,则称
服从向量高斯分布,表示为
。若(1.3)中有
,那么
为正定矩阵,可得y的密度函数 [9]
(1.4)
若(1.3)中有
那么
为非满秩半正定矩阵,对应密度函数可通过矩阵广义逆给出 [10] 。
进一步考虑随机矩阵
,即
的每个元均为随机变量。我们有
定义1.1.1 [9] 称一个随机矩阵
服从矩阵标准正态分布,记为
,若满足以下两条:
(1.5)
(1.6)
其中
分别表示矩阵Z的第i个行向量和第j个列向量。
定义1.1.2 [9] 设随机矩阵
。令
,且
(1.7)
若
与
有相同分布,则称矩阵
服从矩阵高斯分布,表示为
(1.8)
性质1.1.1 [9] 设随机矩阵
,其中
都是正定矩阵。那么
的密度函数为
(1.9)
性质1.1.2 [9] 设
为随机矩阵。那么
当且仅当
(1.10)
其中
是两个(半)正定矩阵的Kronecker积。
证明:由于
为正定或者半正定矩阵,那么
,其中
。令
,其中
,则
。
故
为了引入张量高斯分布,我们下面来介绍有关张量的一些基本概念与记号。
1.2. 张量的背景知识
张量又称多维数组 [11] [12] 。一个
矩阵为2阶张量,一个
阶张量具有m个方向(mode, m-way),记为
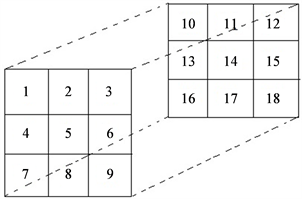
。一个3阶张量
的几何表示如图1。
一个0阶张量为一个标量,一个1阶张量为向量,2阶张量为一个矩阵,3阶或更高阶张量通常称为高阶张量。张量在元素表示上和矩阵相似,其下标个数与其阶数一致。如一个3阶张量
的第
位置的元记为
。
本文通过引进三阶张量高斯分布,实现传统形式下的高斯分布的推广。运用高阶张量,简化随机矩阵的特征函数、矩函数和密度函数等基本概念的表述。
Figure 1. Third order tensor
图1. 3阶张量
2. 预备知识
2.1. 随机向量和随机矩阵的高斯分布
定义2.1.1 [9] (1)一个随机向量
的特征函数为
,矩生成函数为
(2)一个随机矩阵
的特征函数为
,矩生成函数为
定义2.1.2 [10] (1)设给定随机向量
,其元素
独立同分布,那么
服从标准非中心化向量高斯分布,记作
,若
,那么
称为标准中心向量高斯。
(2) 若
,有限的常数矩阵
满足
,
服从向量高斯分布,记作
,其中
,
。
定理2.1.1 [10] (a)一个标准向量高斯分布
有特征函数
,矩生成函数
,均值
,协方差矩阵
。
(b)一个向量高斯分布
有特征函数
,矩生成函数
,均值
,协方差矩阵
。
(c)
的特征函数是
,矩生成函数是
。
定理2.1.2 [10] 若
,其中
,
,
。则
定理2.1.3 设
,其中
为随机矩阵,
为适当大小矩阵。则
(2.1)
其中
表示方阵
的迹(trace),
表示矩阵
的转置。
证明:由特征函数定义知
定义2.1.3 [9] 一个
矩阵
服从矩阵高斯分布,表为
,其中
定义 2.1.4 [10] 条件
等价于以下三条中的任意一条:
(1)
;
(2)
;
(3)
,其中
,
。
定理2.1.4 [10]
是任意
的实矩阵,
,
,
独立同分布,有
,那么Z的特征函数为
定理2.1.5 [10] 若
,常数矩阵
,
,
则
的特征函数为
其中
定理2.1.6 [10] 若
,
是常数矩阵,那么
(2.2)
证明:由定理2.1.1可知
2.2. 张量的预备知识
定义2.2.1 [11] (张量的切片)切片是张量的降维表示。图2给出了一个3阶张量
的三种不同方向上的切片方式,即水平切片(horizontal切片)、左右切片(lateral切片)和前后切片(frontal切片)。类似矩阵A的第
行的表示法
和第j列表示法
,我们用
表示m阶张量
的模-k方向的第i个切片,如
表示3阶张量
模-1方向的第
,
个切片,
表示lateral切片(模-2方向)的第
,
个切片,
表示frontal切片(模-3方向)的第
,
个切片。
类似于矩阵向量化,张量同样可进行矩阵化及向量化。下面我们来定义张量的矩阵化。
定义2.2.2 [12] 把一个3阶张量沿某方向的切片按一定顺序排成矩阵形式的过程称为张量的矩阵化(matricization)。
一个3阶张量有3个不同方向的切片,因此有3种形式的矩阵化,如一个2 × 3 × 4张量的模-1方向切片形成2 × 12的矩阵,同理它在模-2方向和模-3方向切片得到3 × 8和4 × 6矩阵。记张量
沿模-
方向展开得到的矩阵为
。
例 2.2.1 设3阶张量
如图3所示。
则其在模-1、模-2、模-3方向上矩阵化后得到的矩阵分别为
,
,
.
定义2.2.3 [12] 大小
的张量
与矩阵
沿模-n的乘积为大小
的张量
,其元定义为
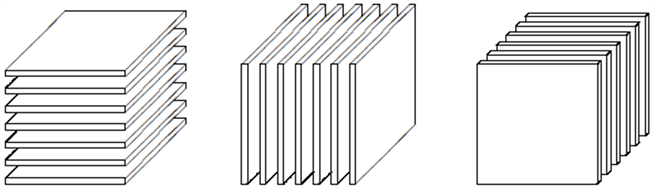 (a) horizontal切片 (b) lateral切片 (c) frontal切片
(a) horizontal切片 (b) lateral切片 (c) frontal切片
Figure 2. Slice of the third order tensor in three different directions
图2. 3阶张量在3个不同方向上的切片
图3. 一个3 × 3 × 2张量A
(2.3)
定理2.2.1 [12] 张量
与矩阵
在模-
方向的乘积的模-
的矩阵化等价于矩阵
与张量
在模-
方向矩阵化后的乘积,即
(2.4)
定理2.2.2. [12] 若
,则有
(2.5)
3. 随机张量的高斯分布
我们可将定理2.1.6改为张量的形式。若
,常数矩阵
,
,
则
。
为了将定理2.1.6推广到三阶张量的一般情况, 我们从随机矩阵的高斯分布出发定义随机张量的高斯分布,并将定理2.1.6中的结论推广到三阶张量。
定义3.1.称
为随机张量,如果每一个
都是随机变量。
定义3.2.称一个三阶随机张量
服从高斯分布,记作
(3.1)
若满足以下三个条件
,
,
其中
表示均值张量,
表示张量
沿第
个方向展开的矩阵的任意一列的协方差矩阵。
定义3.3 .如果(3.1)中的
,那么
称作标准高斯张量。
定理3.1对于三阶张量
,若
,当且仅当
(3.2)
(3.3)
(3.4)
证明:设水平切片(模-1方向)的第
个切片为矩阵
,左右切片(模-2方向)的第
个切片为矩阵
,前后切片(模-3方向)的第
个切片为矩阵
。
由于
,
,
则
,
,
故
,
,
推论3.1.对于三阶张量
,若
,则
(1)
(2)
(3)
证明:利用定义4即可
定理3.2 .若
,矩阵
,
,
,
,那么
(3.5)
证明:由于
,则
令
,则
,则
由定理2.1.6可知
由于
故
基金项目
苏州科技大学研究生科研创新项目(SKYCX16_008)。
文章引用
何玲玲,林泽榕,吴 田,徐常青. 随机张量的高斯分布
On Tensor Gaussian Distributions[J]. 应用数学进展, 2017, 06(08): 1010-1017. http://dx.doi.org/10.12677/AAM.2017.68121
参考文献 (References)
- 1. Chikuse, Y. (2008) The Matrix Angular Central Gaussian Distribution. Journal of Multivariate Analysis, 33, 265-274.
https://doi.org/10.1016/0047-259X(90)90050-R
- 2. 尉迟江. 对高斯分布函数形式的推导[J]. 统计与信息论坛, 2009, 24(5): 3-6.
- 3. 熊焰, 赵铁山. 金融资产收益率分布的混合高斯分布模型[J]. 统计与决策, 2004(12): 26.
- 4. 张乃根. 经济学分析法学的理论基石——“高斯原理”评介[J]. 政治与法律, 1991(2): 54-56.
- 5. 邓改革. 天文时间序列的分析研究[D]: [硕士学位论文]. 广州: 广州大学, 2013.
- 6. 徐甲文, 徐松涛. 指数或高斯分布信号的MSE量化器的简捷设计[J]. 北京航空航天大学学报, 1997(3): 404-408.
- 7. 李建泉. 正态分布高斯推证法释疑[J]. 测绘地理信息, 1991(1): 35-37.
- 8. 王海涌, 费峥红, 王新龙. 基于高斯分布的星像点精确模拟及质心计算[J]. 光学精密工程, 2009, 17(7): 1672-1677.
- 9. Kollo, T. and Von Rosen, D. (2005) Advanced Multivariate Statistics with Matrices. Springer Netherlands, 81-82, 123-135.
- 10. Muller, K.E. and Stewart, P.W. (2006) Linear Model Theory. Wiley-Interscience [John Wiley & Sons], Hoboken, NJ, 7-8.
https://doi.org/10.1002/0470052147
- 11. Kolda, T.G. and Badel, B.W. (2009) Tensor Decompositions and Ap-plications. Sandia Report, 51, 455-500.
https://doi.org/10.1137/07070111X
- 12. Qi, L. and Luo, Z. (2017) Tensor Analysis: Spectral Theory and Spectral Tensors. SIAM.
https://doi.org/10.1137/1.9781611974751








 (a) horizontal切片 (b) lateral切片 (c) frontal切片
(a) horizontal切片 (b) lateral切片 (c) frontal切片