Advances in Applied Mathematics
Vol.
08
No.
07
(
2019
), Article ID:
31442
,
7
pages
10.12677/AAM.2019.87149
Subharmonic Bifurcations and Chaos for the Buckled Beam at Axial Motion
Jing Wang, Dongmei Zhang
School of Mechanics and Statistics, Linyi University, Linyi Shandong

Received: July 4th, 2019; accepted: July 19th, 2019; published: July 26th, 2019

ABSTRACT
The subharmonic bifurcations and chaos for one kind of buckled beam model subjected to parametric excitations are investigated. The critical curves separating the chaotic and non-chaotic regions are obtained by utilizing Melnikov method. The conditions for subharmonic bifurcations are also obtained. Numerical results are given, which verify the analytical ones.
Keywords:Buckled Beam, Subharmonic Bifurcations, Chaos, Melnikov Methods
轴向运动曲梁的次谐分岔和混沌
王晶,张冬梅
临沂大学数学与统计学院,山东 临沂

收稿日期:2019年7月4日;录用日期:2019年7月19日;发布日期:2019年7月26日

摘 要
研究了一类轴向运动屈曲梁的次谐分岔和混沌行为。利用Melnikov方法,给出了屈曲梁异宿轨道Melnikov函数和次谐Melnikov函数的表达式,得到系统出现次谐分岔和超次谐分岔的参数条件,给出系统混沌区域和非混沌区域的分界曲线。根据参数的取值范围做数值模拟,结果验证了理论分析。
关键词 :屈曲梁,次谐分岔,混沌,Melnikov方法

Copyright © 2019 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
屈曲梁结构在军事、航空航天、土木、机械等工程中有广泛的应用,拱形结构当受到动态负荷时,会展示出丰富的动力学现象,包括次谐波、超谐振荡、极限环、混沌运动等 [1] [2]。1983年,Moon [3] [4] 等研究了非线性边界条件下的梁受到周期载荷后的混沌运动。Suire [5] 用数值方法研究了大扰度粘弹性梁的周期和混沌。冯志华,胡海岩研究了内共振条件下直线运动梁的动力稳定性,基于凯恩方程建立非线性动力学方程,得出非线性振动的Hopf分岔以及极限环。Danida [6]、Anantha [7]、Neukirch [8] 等研究了弹性屈曲梁的周期解和混沌动力学行为。张等 [9] [10] 研究了两端简支的非线性弹性梁受周期载荷作用后,发生次谐分岔和混沌运动的条件。Pinto [11] [12] 等分析了弹性屈曲梁在强迫力作用下出现马蹄混沌行为。
本文研究一类轴向载荷作用下梁的次谐分岔和混沌行为,对梁的单模态方程,应用Melnikov方法,得到了系统发生次谐分岔和超次谐分岔的参数范围,及混沌区域和非混沌区域的分界线。
2. 问题描述
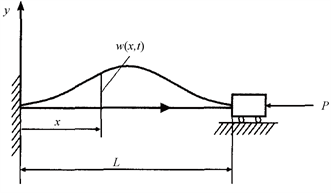
Figure 1. A buckled beam at axial motion
图1. 屈曲梁结构模型
如图1所示,考虑梁的长度为L,横截面积为A,横截转动惯量为J,材料的弹性模量为E,轴向力为P。假定梁的横截面是均匀的,材质均相同.轴向位移采用u表示,横向位移采用w表示,u和w是空间坐标x的函数,文献 [11] 得到弯曲梁的运动方程为
(1)
边界条件为
和 时, ,
利用伽辽金法,单模态的运动方程为
(2)
这里考虑 的情况,令 , , ,则方程(2)变成
(3)
当 时,系统(3)的未扰动系统为
(4)
(4)是Hamiltonian系统,其Hamiltonian量为
(5)
3. 系统的次谐分岔与混沌
的混沌行为
当 时,利用如下变换
, (6)
将(6)代入(3)式,得到
(7)
其中 , , 。当 时,未扰动系统为
(8)
其Hamilton量为
(9)
该系统有三个平衡点,通过定性分析可知, 为(8)的中点, 和 是鞍点。当 时,存在两条连接 的异宿轨道,形成一个异宿环,如图2所示。
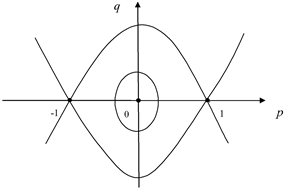
Figure 2. The phase portrait of system (8)
图2. 系统(8)的相图
该异宿轨道的参数表达式为
(10)
以 为参数的周期轨道为
(11)
其中sn,dn,cn为Jacobian椭圆函数,k为椭圆函数的模, ,k满足关系式 ,定义轨道的周期为 , 是第一类完全椭圆积分。
下面计算系统(7)沿着异宿轨道的Melnikov函数
(12)
其中
,
由(12)可知,当参数 , 满足
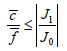 (13)
(13)
即参数 满足参数条件
存在零点,系统发生混沌。取不同的 值,比如 ,得到系统发生混沌的临界曲线,如图3所示。在曲线下方是发生混沌的区域,在曲线上方是非混沌区域。
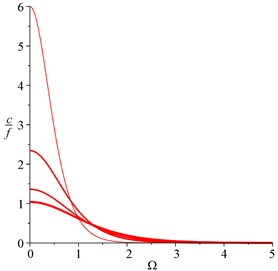
Figure 3. The critical curves for chaotic motions
图3. 系统发生混沌的临界曲线
4. 通向混沌的道路
对于任给的一对互素的正整数 ,存在唯一的k,满足 ,沿这个周期为 的轨道计算次谐波Melnikov函数得
(14)
其中
(15)
(16)
, 为第二类椭圆积分。
当参数满足条件
(17)
系统发生奇数阶次谐分岔。
5. 数值模拟
对系统(2)使用龙格库塔法做数值模拟来验证屈曲梁是否存在混沌现象。根据前面理论的分析来选取参数
,
,
, ,
,初始点选取为
,
,初始点选取为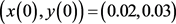 ,相图和时间历程图如图4所示。再令参数
,其它参数值不变,得到系统相图和时间历程图如图5所示。
,相图和时间历程图如图4所示。再令参数
,其它参数值不变,得到系统相图和时间历程图如图5所示。
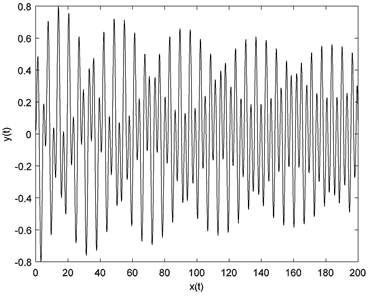
Figure 4. The phase portrait of system (2) for
图4. 当 时,系统的相轨迹图和时间历程图

Figure 5. The phase portrait of system (2) for
图5. 当 时,系统的相轨迹图和时间历程图
6. 结论
研究了受轴向载荷和附加载荷弹性屈曲梁的次谐分岔和混沌行为。利用Melnikov方法,给出了屈曲梁同宿轨道Melnikov函数和次谐Melnikov函数的表达式,得到系统出现次谐分岔和超次谐分岔的参数条件,给出系统混沌区域和非混沌区域的分界曲线。根据参数的取值范围做数值模拟,结果验证了理论分析。
基金项目
本论文受山东省自然科学基金资助(ZR2018MA002)和2018大学生创新创业项目资助(51819220)。
文章引用
王 晶,张冬梅. 轴向运动曲梁的次谐分岔和混沌
Subharmonic Bifurcations and Chaos for the Buckled Beam at Axial Motion[J]. 应用数学进展, 2019, 08(07): 1277-1283. https://doi.org/10.12677/AAM.2019.87149
参考文献
- 1. Abou-Rayan, A.M., Nayfeh, A.H., Mook, D.T., et al. (1993) Nonlinear Response of a Parametrically Excited Buckled Beam. Non-linear Dynamics, 4, 499-525.
https://doi.org/10.1007/BF00053693 - 2. Afaneh, A.A. and Ibrahim, R.A. (1993) Nonlinear Response of a Initially Buckled Beam with 1:1 Internal Resonance to Sinusoidal Excitation. Nonlinear Dynamics, 4, 547-571.
https://doi.org/10.1007/BF00162232 - 3. Moon, F.C. and Shaw, S.W. (1983) Chaotic Vibration of a Beam with Nonlinear Boundary Conditions. Non-Linear Mechanics, 18, 465-477.
https://doi.org/10.1016/0020-7462(83)90033-1 - 4. Moon, F.C. (1988) Experiments on Chaotic Motions of a Forced Nonlinear Oscillator. Stranger Attractors. Journal of Applied Mechanics, 55, 190-196.
- 5. Suire, G. and Cederbaum, G. (1995) Periodic and Chaotic Behavior of Viscoelastic Nonlinear Bars under Harmonic Excitations. International Journal of Mechanical Sciences, 7, 753-772.
https://doi.org/10.1016/0020-7403(95)00006-J - 6. Danida, D.B. (1994) Mathematical Models Used in Studying the Chaotic Vibration of Buckled Beam. Mechanics Research Communications, 21, 321-335.
https://doi.org/10.1016/0093-6413(94)90091-4 - 7. Anantha, R.S., Sunkar, T.S. and Ganean, S. (1994) Bifurcation, Catastro-phes and Chaos in a Pre-Buckled Beam. International Journal of Non-Linear Mechanics, 29, 449-462.
https://doi.org/10.1016/0020-7462(94)90014-0 - 8. Neukirch, S., Frelat, J., Goriely, A., et al. (2012) Vibrations of Post-Buckled Rods: The Singular Inextensible Limit. Journal of Sound and Vibration, 331, 704-720.
https://doi.org/10.1016/j.jsv.2011.09.021 - 9. 张年梅, 杨桂通. 非线性弹性梁的动态次谐分岔与混沌运动[J]. 非线性动力学学报, 1996(3): 265-274.
- 10. 张年梅, 杨桂通. 非线性弹性梁中的混沌带现象[J]. 应用数学和力学, 2003, 24(5): 450-454.
- 11. Pinto, O.C. and Goncalves, P.B. (2002) Active Non-Linear Control of Buckling and Vibrations of a Flexible Buckled Beam. Chaos Solitons and Fractals, 14, 227-239.
https://doi.org/10.1016/S0960-0779(01)00229-6 - 12. Oumarou, A.S., Nana Nbendjo, B.R. and Woafo, P. (2011) Appearance of Horseshoes Chaos on a Buckled Beam Controlled by Disseminated Couple Forces. Communication in Nonlinear Science Numerical Simulation, 16, 3212-3218.
https://doi.org/10.1016/j.cnsns.2010.11.010