Advances in Applied Mathematics
Vol.
08
No.
11
(
2019
), Article ID:
33077
,
7
pages
10.12677/AAM.2019.811209
Nonlinear Integral Equation Solution Based on Radial Basis Function Interpolation
Binbin Wang, Guang Zeng*, Li Lei, Han Xiong
East China University of Technology, Nanchang Jiangxi

Received: Oct. 29th, 2019; accepted: Nov. 14th, 2019; published: Nov. 21st, 2019

ABSTRACT
The radial basis function (RBF) interpolation is applied to the solution of the nonlinear integral equation. In this paper, the multiquadric (MQ) function with excellent interpolation performance in RBF is selected. First, the function to be solved is expressed as a linear combination of RBF, and then the equation is discretized into a non-linear square by collocation method. The approximate expression of the function to be solved is given after the weight coefficients obtained. Solving nonlinear integral equation based on MQ function interpolation can obtain higher accuracy with fewer nodes, which can be extended to high-dimensional integral equation. In this paper, we prove the existence and uniqueness of MQ basis function interpolation problem, and analyse the interpolation basis function of constructing non-linear function of MQ function by numerical examples, and obtain the ideal approximation effect and result.
Keywords:Radial Basis Function, MQ Function, Interpolation, Shape Parameter, Numerical Integration
基于径向基函数插值的非线性积分方程求解
王斌斌,曾光*,雷莉,熊晗
东华理工大学理学院,江西 南昌

收稿日期:2019年10月29日;录用日期:2019年11月14日;发布日期:2019年11月21日

摘 要
将径向基函数(radialbasisfunction, RBF)插值应用于非线性积分方程的求解中,本文选用的是RBF中插值性能优异的多重二次曲面(multiquadric, MQ)函数,首先将待求函数表示为RBF的线性组合,再通过配置法将方程离散为非线性方程组,求得权系数后给出待求函数的近似表示。基于MQ函数插值求解非线性积分方程可以在较少的节点下得到更髙的精度,且可扩展到髙维的积分方程中。本文证明了MQ基函数插值问题的存在唯一性,并且通过数值算例对MQ函数构造非线性函数的插值基函数进行了分析,得到了理想的逼近效果。
关键词 :径向基函数,MQ函数,插值,形状参数α,数值积分

Copyright © 2019 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
许多科学工程问题的数学模型最终都可归结为积分方程的求解问题。相对于微分方程,积分方程能够将初值和边值信息包含在同一方程中,且数值积分计算引起的相对误差远小于数值微分,因此有望得到更高精度的数值解。积分方程的一般形式为
(1)
式中, 为自由项, 为核函数, 为待求函数的已知泛函, 为积分区域, 为已知参数。根据 的形式分为线性和非线性两类,由积分限又可分为Fredholm和Volterra两类积分方程。积分方程的经典数值解法包括待定系数逼近法、直接数值求积法、逐步逼近法以及针对特定积分核的近似解法等。
随着积分方程的发展,很多新方法正逐步引入积分方程的数值求解中,如用伽辽金方法、配点法并结合Haar小波函数求解第一类线性Fredholm方程 [1],用Haar小波方法求解一维 [2] 和二维 [3] 非线性方程问题,然而计算误差相对较大;用Daubechie小波并结合伽辽金方法来求解第二类线性Volterra方程问题 [4];或应用Sinc函数配置法求解一维第一类线性 [5] 和非线性Fredholm方程 [6];用修正的块脉冲函数求解第一类Volterra积分方程 [7],及应用块脉冲函数和泰勒级数结合求解非线性Fredholm-Volterra方程 [8];应用Chebyshev配置法求解二维线性方程问题 [9],或应用块脉冲法求解二维Fredholm-Volterra [10] 以及用多项式近似方法 [11] 快速求解具有光滑核函数的第二类Fredholm积分。上述数值求解方法多采用了级数形式、Chebyshev多项式或小波函数等,但由于多项式函数空间的刚性过强,易造成插值效果不稳定;又因为小波的插值误差相对较大,且在二维及多维问题中难以构造岀合适的插值基函数。因此,需要一种插值精度高且适合多维问题的基函数。
径向基函数(radial basis function, RBF)最初在1968年由Hardy在地形学中提岀并适用于多维散布数据插值,它对空间维数不敏感且插值精度较高,因而在多元插值中得到广泛的应用 [12]。1990年,Kansa [13] 首次将RBF成功应用于微分方程的求解中并逐步形成一类配点型无网格法。目前RBF插值理论研究已成为一个热点问题,本文尝试将RBF方法应用到积分方程的求解中,基于RBF插值逼近原理,提岀了RBF求解一维非线性积分方程的方法,给岀了数值算例并与其他数值方法进行对比,得到了较好的逼近效果。
2. 基于RBF插值改进的配置法算法
2.1. RBF插值原理
定理2.1 [14] 设函数 连续且满足 ,对于任给的点 ,插值问题存在
唯一解充要条件矩阵 是正定矩阵。
对空间 中的变元x,定义函数 ,并且假设该函数可由Fourier积分表示;
,当 两两不同且 不全为零时,有
(2)
考虑到定理2.1,对任意两两不同的点 ,径向基插值存在唯一解充要条件为:函数 的Fourier变换 几乎处处非负,且至少在某个正测度集上大于零。此时称函数 为空间 上的正定函数。一般的若函数 是空间 上的正定函数,并不能得 是空间 上的正定函数.如下定理指岀:在一定条件下,函数 在任意维空间上都是正定的。
定理2.2 [14] 设 ,函数 对任意空间都正定的充要条件 是完全单调函数,即:
(1) ;
(2) ;
(3) 。
由此定理可知,Gauss函数和IMQ函数在任意维空间都是正定函数,而MQ函数和薄板样条则不然,可以证明,MQ函数与薄板样条的广义Fourier变换仍大于零,但是其在原点有奇性,如果奇点的阶数为m,对满足 的系数 有
(3)
这类 函数被称为m阶条件正定函数,对m阶条件正定函数 ,若矩阵 列满秩,则分块矩阵
可逆,此时,径向基插值问题可叙述为:给定数据 ,寻找具体如下形式的函数
(4)
满足
(5)
2.2. 基于RBF插值的改进配置法算法
RBF是仅依赖于距离 的函数,在多种RBF的定义中,常用的有薄板样条函数 高斯函数 、Hardy提岀的多重二次曲面(multi-quadric, MQ)函数及多种紧支撑函数等。Franke在1982年证明了MQ方法是所有插值方法中综合性能最优的,因此本文选用MQ作为插值基函数,其常用表达式为
(6)
式中c是基函数中心, 称为形状参数。算法步骤具体为:
Step 1:设置RBF函数的中心点c,形状参数 ,配置点 ;
Step 2:对给定的一组数据点 ,由RBF构造插值函数
(7)
Step 3:将插值点代入(7)式,得
(8)
表示成矩阵形式为
(9)
式中 为给定数据点的函数值, 为待定系数, 为插值矩阵。
Step 4: 矩阵元素计算式为 ,求解(9)式得
(10)
Step 5: 得岀函数 的RBF逼近形式
(11)
3. Multi-Quadric函数插值的存在性与唯一性
定义3.1 [15] MQ函数的插值问题:对于给定的多元散乱数据 。采用函数 的平移作为一组基函数 ,寻找形如:
的插值函数 ,且使其满足条件:
引理3.2 [16] 若MQ函数 在
上连续,且
,那么对于n元的MQ基函数插值问题的
在
上连续,且
,那么对于n元的MQ基函数插值问题的
解满足存在唯一性的充要条件为系数矩阵 是正定矩阵。
定理3.3 若MQ函数 是连续的,且 ,那么对于n元的MQ基函数插值问题存在唯一解。
证明:对于d元Gauss函数 ,对于任意两两不同的 和不全为零的 ,有
因此Gauss函数是正定的。
再讨论分析 ,它是一个可积函数的积分。由Gauss函数的正定性可知,对
于不全为零的 ,若 可得二次型
其中h是正常数,所以得
由此知道MQ函数是零阶条件负定的,那么其插值系数矩阵 至少有n − 1个特征向量
是对应于负特征值的。当 时,有
所以插值系数矩阵 有n个非零特征值,即此系数矩阵是非奇异矩阵,故所对应的插
值问题满足存在唯一性。
4. 数值实验及分析
径向基函数在数值逼近领域有着广泛的应用,本节将介绍径向基函数插值在具体函数方程中的应用,这里应用MQ基函数对函数 插值,其中 。
用函数 进行插值,寻找插值函数
, (12)
使得
(13)
观察(13)式,发现其是关于系数 的一元非齐次线性方程组,由于系数矩阵
非奇异,故此方程组有唯一解,可求出 ,代入(12)式得到 ,进而求出插值函数。下面给出了误差表1及两种插值图1,图2。
在数值模拟中,本文选择了 为待逼近函数进行数值实验。基于MQ径向基函数插值方法,分别选择插值节点 ,步长 ,且配置点与中心点一致进行数值算例模拟,计算结果如图1和图2。从图1及图2的插值图像可知,基于MQ径向基函数插值方法是有效的,且具有较高的精度。此外,表1还列出了本文方法与文献 [6] [12] [17] 方法的最大误差比较结果,从表中数据可以看出,本文方法对比于其他的数值方法得到的误差更小,稳定性更高。
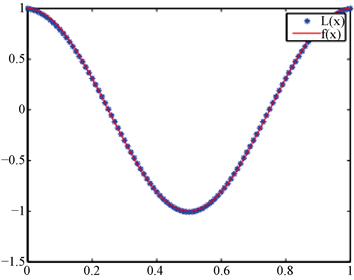
Figure 1. , function image
图1. 时, 函数图像
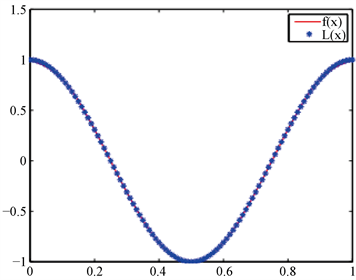
Figure 2. , function image
图2. 时, 函数图像
Table 1. The maximum error comparison between the method in this paper and the methods in [6] [12] [17]
表1. 本文方法与文献 [6] [12] [17] 方法的最大误差比较
5. 结论
本文给出了一种基于MQ径向基函数求解非线性积分方程的方法,且证明了该方法的存在唯一性,并通过上述数值算例验证了该方法是行之有效的,且精度较高;MQ径向基函数是一个距离的函数,在高维插值时只需改变距离的计算式,不必变化算法的其他部分,因此有利于推广到高维的非线性积分方程的求解中。由于MQ径向基函数插值性能优异,能够在较少的节点下得到更高的逼近精度,因而计算量较小且操作简洁。本文还尚未对形状参数 的选取、算法的误差限等问题进行更加细致的理论分析,这也将是今后研究的一个重要方向。
基金项目
国家自然科学基金资助项目(11661005;11301070);东华理工大学校级教改课题(DHJG-07-39;DHJG-18-47)。
文章引用
王斌斌,曾 光,雷 莉,熊 晗. 基于径向基函数插值的非线性积分方程求解
Nonlinear Integral Equation Solution Based on Radial Basis Function Interpolation[J]. 应用数学进展, 2019, 08(11): 1795-1801. https://doi.org/10.12677/AAM.2019.811209
参考文献
- 1. Rabbani, M., Maleknejad, K., Aghazadeh, N. and Mollapourasl, R. (2007) Computational Projection Methods for Solving Fredholm Integral Equation. Applied Mathematics and Computation, 191, 140-143.
https://doi.org/10.1016/j.amc.2007.02.071 - 2. Aziz, I. and Sirai-ul-islam (2013) New Algorithms for the Numerical Solution of Nonlinear Fredholm and Volterra Integral Equations Using Haar Wavelets. Journal of Computational and Applied Mathematics, 239, 333-345.
https://doi.org/10.1016/j.cam.2012.08.031 - 3. Babolian, E., Bazm, S. and Lima, P. (2011) Numerical Solution of Nonlinear Two-Dimensional Integral Equations Using Rationalized Haar Functions. Communications in Nonlinear Science and Numerical Simulation, 16, 1164-1175.
https://doi.org/10.1016/j.cnsns.2010.05.029 - 4. Saberi-nadjafi, J., Mehrabinezhad, M. and Akbari, H. (2012) Solving Volterra Integral Equations of the Second Kind by Wavelet-Galerkin Scheme. Computers and Mathematics with Applications, 63, 1536-1547.
https://doi.org/10.1016/j.camwa.2012.03.043 - 5. Maleknejad, K., Mollapourasl, R. and Alizadeh, M. (2011) Convergence Analysis for Numerical Solution of Fredholm Integral Equation by Sinc Approximation. Communications in Nonlinear Science and Numerical Simulation, 16, 2478-2485.
https://doi.org/10.1016/j.cnsns.2010.09.034 - 6. Maleknejad, K. and Nedaiasl, K. (2011) Application of Sinc-Collocation Method for Solving a Class of Non-Linear Fredholm Integral Equations. Computers & Mathematics with Applications, 62, 3292-3303.
https://doi.org/10.1016/j.camwa.2011.08.045 - 7. Maleknejad, K. and Rahimi, B. (2011) Modification of Block Pulse Functions and Their Application to Solve Numerically Volterra Integral Equation of the First Kind. Communications in Nonlinear Science and Numerical Simulation, 16, 2469-2477.
https://doi.org/10.1016/j.cnsns.2010.09.032 - 8. Mirzaee, F. and Hoseini, A. (2013) A Numerical Solution of Nonlinear Volterra-Fredholm Integral Equations Using Hybrid of Block-Pulse Functions and Taylor Series. Alerandria Engineering Journal, 52, 551-555.
https://doi.org/10.1016/j.aej.2013.02.004 - 9. Babolian, E., Abbasbandy, S. and Fattahzadeh, F. (2008) A Numerical Method for Solving a Class of Functional and Two Dimensional Integral Equations. Applied Mathematics and Computation, 198, 35-43.
https://doi.org/10.1016/j.amc.2007.08.051 - 10. Babolian, E., Maleknejad, K., Mordad, M. and Rahimi, B. (2011) A Numerical Method for Solving Fredholn-Volterra Integral Equations in Two-Dimensional Spaces Using Block Pulse Functions and an Operational Matrix. Journal of Computational and Applied Mathematics, 235, 3965-3971.
https://doi.org/10.1016/j.cam.2010.10.028 - 11. Xie, W.J. and Lin, F.R. (2009) A Fast Numerical Solution Method for Two Dimensional Fredholm Integral Equations of the Second Kind. Applied Numerical Mathematics, 59, 1709-1719.
https://doi.org/10.1016/j.apnum.2009.01.009 - 12. Tang, T., Xu, X. and Cheng, J. (2008) On Spectral Methods for Volterra Integral Equations and the Convergence Analysis. Journal of Computational Mathematics, 26, 825-837.
- 13. Kansa, E.J. (1990) Multiquadrics—A Scattered Data Approximation Scheme with Applications to Computional Fluid Dynamics I. Surface Approximations and Partial Derivative Estimates. Computers and Mathematics with Applications, 19, 127-145.
https://doi.org/10.1016/0898-1221(90)90270-T - 14. 吴宗敏. 径向基函数、散乱数据拟合与无网格偏微分方程数值解[J]. 工程数学学报, 2012, 19(2): 1-12.
- 15. 徐敏. 样条函数与径向基函数逼近某些问题的研究[D]: [博士学位论文]. 大连: 大连理工大学, 2010.
- 16. 吴宗敏. 散乱数据拟合的模型、方法和理论[M]. 北京: 科学出版社, 2007.
- 17. 张淮清, 陈玉, 聂鑫. 基于径向基函数插值的积分方程求解[J]. 应用数学与计算数学学报, 2017, 31(3): 275-289.
NOTES
*通讯作者。
