Advances in Applied Mathematics
Vol.
09
No.
01
(
2020
), Article ID:
33968
,
5
pages
10.12677/AAM.2020.91012
Explicit Exact Solutions for a Nonlinear Reaction-Diffusion Equation
Liangbo Lv
School of Mathematics and Information Science, Guangzhou University, Guangzhou Guangdong

Received: Dec. 26th, 2019; accepted: Jan. 8th, 2020; published: Jan. 15th, 2020

ABSTRACT
In this paper, a nonlinear reaction-diffusion equation is reduced to the standard heat equation by seeking appropriate nonlinear transformation and solves reduced equations with a variable separation approach, finally, through the inverse transformation of the nonlinear transformation, some new explicit exact solutions can be obtained.
Keywords:Nonlinear Reaction-Diffusion Equation, Variable Separation Approach, Nonlinear Transformation, Explicit Exact Solutions

一个非线性反应扩散方程的显式精确解
吕良博
广州大学数学与信息科学学院,广东 广州
收稿日期:2019年12月26日;录用日期:2020年1月8日;发布日期:2020年1月15日

摘 要
本文首先通过找到合适的非线性变换将一个非线性反应扩散方程化简为标准的热传导方程,然后利用变量分离法求解这个标准的热传导方程,最后通过这个非线性变换的逆变换得到非线性反应扩散方程丰富的显式精确解。
关键词 :非线性反应扩散方程,变量分离法,非线性变换,显式精确解

Copyright © 2020 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
众所周知,非线性偏微分方程广泛应用于海洋工程、光纤通信、等离子体物理、化学物理等诸多科学领域,同时,非线性偏微分方程精确解的研究工作在非线性科学中具有十分重要的意义。近年来,相继涌现出一些研究偏微分方程非线性系统精确解的方法,如Hirota双线性方法 [1],Backlund变换方法 [2],齐次平衡法 [3] [4],变量分离方法 [5] [6],反演散射方法 [7],正弦余弦方法 [8] [9] 等。非线性偏微分方程的求解是一个十分重要但极其困难的问题,至今为止都没有一种普遍适用、行之有效的方法,一般来说,首先可以通过假设目标方程解的形式或者变量变换等手段来约化目标方程,将目标方程转换到我们较为熟悉的线性偏微分方程或者常微分方程(组)的形式,通过求解这些线性偏微分方程或者常微分方程(组)从而得到目标方程的精确解。然而在很多情况下非线性偏微分方程经过一个合适的变换会被约化成一系列由多个偏微分方程组成的超定非线性偏微分方程组 [10] [11]。
接下来我们讨论如下非线性反应扩散方程:
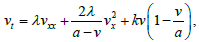 (1.1)
(1.1)
其中, 是任意常数,且 ,这个非线性反应扩散方程经常出现在微分几何、化学以及动力学等领域,常用于描述粒子运动、生物菌落成长等现象 [12] [13],近年来受到许多学者的关注。关于非线性反应扩散方程(1.1)可积性、精确解方面已有一些研究 [14] [15] [16],然而相对而言这方面研究较少,本文的目的在于得到非线性反应扩散方程(1.1)丰富的精确解,从而为非线性反应扩散方程(1.1)的相关理论研究做一些补充和拓展,为相关领域的数值计算的准确性提供检验。
2. 相应的非线性变换
为了化简目标方程(1.1),需要找到合适的非线性变换,首先考虑如下方程:
(2.1)
称方程(2.1)为方程(1.1)的母方程,而方程(1.1)称为方程(2.1)的生成方程;接下来希望找到一个能够将非线反应扩散方程(1.1)转化成母方程(2.1)的变换,由方程(2.1)出发,首先作变换:
(2.2)
其中 是待定光滑函数,由此计算可得:
(2.3)
(2.4)
将等式(2.3)、(2.4)代入方程(2.1),可得:
(2.5)
不失一般性,这里我们令 ,可以得到一个与反应扩散方程(1.1)形式对应的方程:
 (2.6)
(2.6)
对照方程(1.1)和(2.6),要找到这个非线性变换,只需满足下列条件:
(2.7)
通过求解常微分方程组(2.7)我们找到如下变换:
(2.8)
换言之,方程(1.1)可以通过变换(2.8)的逆变换 化简至方程(2.1),为了进一步化简方程(2.1),首先对方程(2.1)两边同时乘以 ,可得如下方程:
(2.9)
再通过变换:
(2.10)
即可将方程(2.9)化简为一般的热传导方程:
(2.11)
综合考虑(2.8)、(2.10)我们可以发现:通过非线性变换:
(2.12)
便可以将方程(1.1)转化为热传导方程(2.11)。
3. 显式精确解
本节首先利用变量分离法求出热传导方程(2.11)的一些显式精确解,再根据非线性变换(2.12)便可以得到非线性反应扩散(1.1)丰富的显式精确解。
运用变量分离的思想,假设热传导方程(2.11)有乘积形式的变量分离解:
(3.1)
其中 是待定光滑函数。
将(3.1)代入到方程(2.11),可得:
(3.2)
整理等式(3.2)得:
(3.3)
对于等式(3.3),等式右边是关于空间变量x的函数,与时间变量t无关,因此当且仅当等式两端都等于一个常数时,方程(3.3)成立,不妨设这个常数为 ,可得:
(3.4)
(3.5)
当 时,通过求解方程(3.4)、(3.5)可得:
(3.6)
(3.7)
其中 是常数,综合(3.1)和(2.12)可得非线性反应扩散方程(1.1)的一族显式精确解:
(3.8)
其中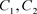 为任意常数。
为任意常数。
当 时,求解常微分方程(3.4)、(3.5)可得通解:
(3.9)
(3.10)
其中 都是任意常数,根据(3.1)和(2.12)可得非线性反应扩散方程(1.1)另一族显式精确解:
(3.11)
其中 为任意常数。
为任意常数。
当 时,运用与上面相同的步骤可以求得如下显式精确解:
(3.12)
根据文献 [13] 的方法,我们可以找到热传导方程(3.1)如下显式精确解:
(3.13)
(3.14)
(3.15)
其中 可取任意常数,i为虚数单位。根据非线性变换(2.12)即可找到关于方程(1.1)的一些显式精确解:
(3.16)
(3.17)
(3.18)
4. 结论与讨论
通过利用非线性变换将非线性反应扩散方程(1.1)转化为一个标准的热传导方程,然后运用变量分离法得到非线性反应扩散方程(1.1)丰富的精确解。这些结果可以为非线性反应扩散方程(1.1)相关领域的定性理论研究提供一些启示和数据帮助,为相关领域的数值计算方面提供检验数值解精确程度、数值格式类型的具体算例。
文章引用
吕良博. 一个非线性反应扩散方程的显式精确解
Explicit Exact Solutions for a Nonlinear Reaction-Diffusion Equation[J]. 应用数学进展, 2020, 09(01): 100-104. https://doi.org/10.12677/AAM.2020.91012
参考文献
- 1. Jimbo, M. and Miwa, T. (1983) Solitons and Infinite Dimensional Lie Algebras. Publications of the Research Institute for Mathematical Sciences, 19, 943-1001.
https://doi.org/10.2977/prims/1195182017 - 2. Beal, R., Rabelo, M. and Tenenblat, K. (1988) Bäcklund Transformations and Inverse Scattering and for Some Pseudo-Spherical Surface Equations. Studies in Applied Mathematics, 81, 125-151.
https://doi.org/10.1002/sapm1989812125 - 3. Wazwaz, A.M. (2013) On the noulocal Boussinesq Equation: Multiple-Soliton Solutions. Applied Mathematics Letters, 26, 1094-1098.
https://doi.org/10.1016/j.aml.2013.06.008 - 4. Senthilvelan, M. (2001) On the Extended Applications of Homogeneous Balance Method. Applied Mathematics and Computation, 123, 381-388.
https://doi.org/10.1016/S0096-3003(00)00076-X - 5. Fan, E. and Zhang, H. (1998) A Note on the Homogeneous Balance Method. Physics Letters A, 246, 403-406.
https://doi.org/10.1016/S0375-9601(98)00547-7 - 6. Kong, L.Q. and Dai, C.Q. (2015) Some Discussions about Variable Separations of Nonlinear Models Using Riccati Equation Expansion Method. Nonlinear Dynamics, 81, 1553-1561.
https://doi.org/10.1007/s11071-015-2089-y - 7. Zhang, S., Lou, S. and Qu, C. (2002) Variable Separation and Exact Solutions to Generalized Nonlinear Diffusion Equations. Chinese Physics Letters, 19, 1741-1744.
https://doi.org/10.1088/0256-307X/19/12/301 - 8. Wazwaz, A.M. (2005) Exact Solutions to the Double Sinh-Gordon Equation by the Tanh Method and a Variable Separated ODE Method. Computers & Mathematics with Applications, 50, 499-508.
https://doi.org/10.1016/j.camwa.2005.05.010 - 9. Wazwaz, A.M. (2004) A Sine-Cosine Method for Handling Nonlinear Wave Equation. Mathematical and Computer Modelling, 40, 499-508.
https://doi.org/10.1016/j.mcm.2003.12.010 - 10. 范恩贵, 张鸿庆. Whitham-Broer-Kaup浅水波方程的Bäcklund变换和精确解[J]. 应用数学与力学, 1998, 19(8): 667-670.
- 11. Shang, Y.D., Huang, Y. and Yuan, W.J. (2011) Bäcklund Transformations and Abundant Exact Explicit Solutions of the Sharma-Tasso-Olver Equation. Applied Mathematics and Computation, 217, 7172-7183.
https://doi.org/10.1016/j.amc.2011.01.115 - 12. Grimson, M.J. and Barker, G.C. (1994) Continuum Model for the Spatiotemporal Growth of Bacterial Colonies. Physical Review E, 49, 1680-1684.
https://doi.org/10.1103/PhysRevE.49.1680 - 13. Wang, D.S. and Zhang, Z.F. (2009) On the Integrability of the Generalized Fisher-Type Nonlinear Diffusion Equation. Journal of Physics A: Mathematical and Theoretical, 42, Article ID: 035209.
https://doi.org/10.1088/1751-8113/42/3/035209 - 14. Wang, X.Y., Fan, S. and Kyu, T. (1997) Complete and Exact Solutions of a Class of Nonlinear Diffusion Equations and Problem of Velocity Selection. Physical Review E, 56, 4931-4934.
https://doi.org/10.1103/PhysRevE.56.R4931 - 15. Bindu, P.S., Senthilvelan, M. and Lakshmanan, M. (2001) Singularity Structure, Symmetries and Integrability of Generalized Fisher Type Nonlinear Diffusion Equation. Journal of Physics A: Mathematical and General, 34, 689-696.
https://doi.org/10.1088/0305-4470/34/49/101 - 16. Feng, Z.S. (2008) Traveling Wave Behavior for a Generalized Fisher Equation. Chaos, Solitons and Fractals, 38, 481-488.
https://doi.org/10.1016/j.chaos.2006.11.031