Advances in Applied Mathematics
Vol.
09
No.
12
(
2020
), Article ID:
39429
,
10
pages
10.12677/AAM.2020.912256
矩阵代数上的2-局部Lie导子
高永兰*,安润玲
太原理工大学数学学院,山西 晋中

收稿日期:2020年11月21日;录用日期:2020年12月20日;发布日期:2020年12月28日

摘要
设
, 分别是矩阵代数和上三角矩阵代数。本文证明若
是2-局部Lie导子,则存在
和映射
使得
(*)其中
。利用该结论证明了
到自身的每个2-局部Lie导子具有形式(*)。证明了若
是2-局部Lie导子,且
,则L具有形式(*),并举例说明条件
不可去。本文还刻画了
到自身的2-局部Lie导子。
关键词
导子,Lie导子,2-局部Lie导子

2-Local Lie Derivations on Matrix Algebras
Yonglan Gao*, Runling An
Department of Mathematics, Taiyuan University of Technology, Jinzhong Shanxi

Received: Nov. 21st, 2020; accepted: Dec. 20th, 2020; published: Dec. 28th, 2020

ABSTRACT
Let
be a matrix algebra, and
be an upper triangular matrix algebra. In this paper, we show that, if
is a 2-local Lie derivation, then there exist a matrix
and a map
such that
(*) where
. As its application, we show every 2-local Lie derivation from
into itself has the form (*). In addition, we show that, if
is a 2-local Lie derivation and satisfies
, then L has the form (*). An example is given to show that the condition
is necessary. 2-local Lie derivations from
into itself are also characterized.
Keywords:Derivations, Lie Derivations, 2-Local Lie Derivations

Copyright © 2020 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
设
是结合代数,
为
的中心。称线性映射
为导子,若等式
成立,称
为内导子,若存在
,等式
成立。近年来,随着不同代数结构上导子理论的丰富和发展,专家学者开始关注映射的局部性质,其中有趣的问题是局部映射在什么条件下能够成为全局的映射或者在何种代数上的局部映射是全局映射。关于局部导子的研究,其奠基者是R. Kadison [1],D. Larson和A. Sourour [2],称线性映射
为局部导子,若对
,存在依赖于A的导子
使得
。过去十多年里,局部导子的研究已经取得了很多深刻的结果 [1] [2] [3] [4]。1997年,P. Semrl在文献 [5] 中首次研究了代数上的2-局部导子,称映射(无线性或连续假设)
为2-局部导子,若对
,存在依赖于A,B的导子
使得
,。P. Semrl [5] 刻画了无限维可分Hilbert空间上的所有有界线性算子构成的代数B(H)上的这类映射,后来,文献 [6] 用比较短的证明方法刻画了有限维的情况下此类映射的结构,得到了类似的结果。关于2-局部导子的结论,文献 [7] 中作者证明了当
时,
到
的2-局部导子是导子,其中
是有单位元的Banach代数,满足任意从
到
的双模
的Jordan导子是导子。
与代数上的一般积相关的是导子,而关于代数上的Lie积可以定义Lie导子。称线性映射
为Lie导子,若
,其中
为A,B的Lie积。Lie导子L是标准的,若存在导子
和线性映射
使得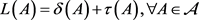 ,其中
,。类似于局部导子和2-局部导子,自然地可以定义局部Lie导子和2-局部Lie导子,文献 [8] 首次提出了局部Lie导子和2-局部Lie导子的概念,称线性映射
为局部Lie导子,若对
,存在依赖于A的Lie导子
使得
。映射(无线性或连续假设)
称为2-局部Lie导子,若对
,存在依赖于A,B的Lie导子
使得
,。相比于2-局部导子的研究,2-局部Lie导子的研究还相对较少,陆芳言教授 [8] 研究了维数大于2的Banach空间X上的有界线性算子全体构成的代数B(X)上的这两类映射,证明了2-局部Lie导子
具有形式
,其中
,。类似于局部导子和2-局部导子,自然地可以定义局部Lie导子和2-局部Lie导子,文献 [8] 首次提出了局部Lie导子和2-局部Lie导子的概念,称线性映射
为局部Lie导子,若对
,存在依赖于A的Lie导子
使得
。映射(无线性或连续假设)
称为2-局部Lie导子,若对
,存在依赖于A,B的Lie导子
使得
,。相比于2-局部导子的研究,2-局部Lie导子的研究还相对较少,陆芳言教授 [8] 研究了维数大于2的Banach空间X上的有界线性算子全体构成的代数B(X)上的这两类映射,证明了2-局部Lie导子
具有形式
,, (*)
其中
, 是齐次映射,满足
,而其证明方法依赖于B(X)上秩一算子的存在性。文献 [9] 作者运用新的方法证明了维数大于4的半有限因子von Neumann代数上的2-局部Lie导子具有类似的结构。
本文刻画矩阵代数
和上三角矩阵代数
上的2-局部Lie导子。证明若
为2-局部Lie导子,则L具有形式(*)。利用该结论刻画了
到自身的2-局部Lie导子。证明了若
是2-局部Lie导子,且
,则L具有形式(*),并举例说明条件
不可去。本文还刻画了
到自身的2-局部Lie导子。
2. 主要结果及证明
为方便讨论,令
为
的矩阵单位,即
位置为1,其他位置为0的矩阵,
为n阶单位矩阵。设
,,则若
,使得
,则A为对角矩阵。若
,则
(1)
引理2.1 ( [10], Problem230) 若
,,则
。
引理2.2 若
为2-局部Lie导子,则
。
证明 对
,,,存在Lie导子
,使得
。 □
定理2.3 若
为2-局部Lie导子,则存在
和映射
,使得
,,
其中
。
证明 设
为2-局部Lie导子,则对
,存在导子
及线性映射
使得
,,
其中
。因为
上的导子为内导子,故存在
使得
,, (2)
下证(2)中
是唯一确定的。
若
,则
,由引理2.1知
,,所以
是唯一确定的。
令
,,,,则(2)可以重写为
,,(3)
由引理2.2和(3)知
,且
,因为
。
由(3)知对
,存在
使得
,,
令
,,,,则
仍是
上的2-局部Lie导子。由证明
的唯一性给出
的定义知
也满足(3),且
,。
对
及U,存在
使得
,,
因为
,所以由引理2.1知
,故
为对角阵,
,故
。
对
及U,存在
使得
,,
因为
,所以由引理2.1知
,故
为对角阵,
。
对
及V存在
使得
,
因为
,由引理2.1知
,故
形如(1)。由于
的
位置为0,所以
。
对
,,存在内导子
使得
,,
由
知
。因此
即
,,。故
,。
对
,令
,则存在
及线性映射
,,使得
另一方面,
因此
,
由引理2.1知
。因此
,
其中
,且
。 □
下面我们运用类似于定理2.3的方法刻画
上的2-局部Lie导子。
定理2.4若
为2-局部Lie导子,则
i) 存在
及映射
使得
,,且
;
ii) 当
时,存在
及映射
使得
;
特别地,当
时,存在
及线性映射
使得
。
证明i) 由于
上的Lie导子为标准Lie导子 [11],且其上的导子为内导子( [12], Corollary2.6),类似于定理2.3的证明,令
,,则
,,所以
,。
对
,,,存在内导子
及映射
使得
,。因为
,由引理2.1得
,因此
,
故
。
ii) 若
,则由(i)知
,。对
,
记
,则
其中
,。同定理2.3中证明
类似,可得
。故
。
当
时,
,。由
,
知
。由引理2.2知
,因此
是线性映射。 □
下面的例子表明若上三角矩阵代数
上的2-局部Lie导子L不满足条件
,则L不具有定理2.4中的形式。
例2.5 设
为
的上三角矩阵代数,
为线性映射。对任意的
,定义
:
若
;
若
。则L为
上的2-局部Lie导子,但L不满足条件
,L不具有定理2.4中的形式。
事实上对
,
i) 当
时,令
,, 为L定义中的映射,则存在Lie导子
为
,,且
, ;
ii) 当
时,令
,,, 为L定义中的映射,则存在Lie导子
为
,,且
, ;
iii) 当
时,令
,,, 为L定义中的映射,则存在Lie导子
为
,,且
,。类似地若
,令
,,,,则
,。
因此L为
上的2-局部Lie导子。当取
时,
,L不满足条件
。
下证L不具有形式
。若
。
设
,则
。
当
时,由L的定义得
,故
,取
得
,取
得
,所以
。
当
时,由L的定义得
,另一方面
,因此
,矛盾。故L不具有形式
。
定理2.6 i) 若
, 为
的中心,
为
的单位元,
为2-局部Lie导子,则存在
及映射
使得
,其中
。
ii) 若
, 为
的中心,
为
的单位元,
为2-局部Lie导子且对
,,则存在
及映射
使得
,其中
。特别地,当
时,
为线性映射。
证明 为方便讨论,令
,。
对
,存在Lie导子
使得
,,
,
即
,两边同乘以
得
,因此存在
使得
。 (4)
根据2-局部Lie导子的定义,对
和
,存在
和线性映射
使得
,,
对
和
,存在
和线性映射
使得
,,
则
,即
,故
,由于
,则由引理2.1可得
,,,。故
,
则由此式和(4)得
。 (5)
i) 当
时,令
,由于L为2-局部Lie导子,故
也是2-局部Lie导子,由定理2.3知,存在
及映射
使得
, (6)
令
为
, 则由(5)和(6)得
。 (7)
令
,则由(7)得,
。 (8)
对
,令
,则存在
及线性映射
,,使得
另一方面,
因此
,。由引理2.1知
,。因此
,其中
。
ii) 当
时,若对
,,则
,。 (9)
不妨设
,则由(5)有
,
令
,因为L为2-局部Lie导子,所以
也是2-局部Lie导子,由(9)和定理2.4知,存在
和映射
使得(6)成立。同(i)的证明类似,令
,则(7)成立。令
,,则
具有形式(8),且
。
当
时,
,
,
令
,则
。令
,,则对
, 为形式(8),且由于
,故
,,且由引理2.2,
为线性映射。 □
致谢
本文作者衷心感谢审稿人和读者的意见和建议。
文章引用
高永兰,安润玲. 矩阵代数上的2-局部Lie导子
2-Local Lie Derivations on Matrix Algebras[J]. 应用数学进展, 2020, 09(12): 2199-2208. https://doi.org/10.12677/AAM.2020.912256
参考文献
- 1. Kadison, R.V. (1990) Local Derivation. Journal of Algebras, 130, 494-509.
https://doi.org/10.1016/0021-8693(90)90095-6
- 2. Larson, D. and Sourour, A. (1990) Local Derivations and Local Automorphisms. Proceedings of Symposia in Pure Math, 51, 187-194. https://doi.org/10.1090/pspum/051.2/1077437
- 3. Johnson, B.E. (2001) Local Derivations on C*-Algebras Are Derivations. Transactions of the American Mathematical Society, 1, 313-325. https://doi.org/10.1090/S0002-9947-00-02688-X
- 4. Crist, R. (1996) Local Derivations on Operator Algebras. Journal of Functional Analysis, 135, 72-92.
https://doi.org/10.1006/jfan.1996.0004
- 5. Semrl, P. (1997) Local Automorphisms and Derivations on B(H). Proceedings of the American Mathematical Society, 125, 2677-2680. https://doi.org/10.1090/S0002-9939-97-04073-2
- 6. Kim, S.O. and Kim, J.S. (2004) Local Automorphisms and Derivations on Mn. Proceedings of the American Mathematical Society, 132, 1389-1392. https://doi.org/10.1090/S0002-9939-03-07171-5
- 7. Ayupov, S., Kudaybergenov, K. and Alauadinov, A. (2017) 2-Local Derivations on Matrix Algebras and Algebras of Measurable Operators. Advances in Operator Theory, 2, 494-505.
- 8. Chen, L., Lu, F.Y. and Wang, T. (2013) Local and 2-Local Lie Derivations of Operator Algebras on Banach Spaces. Integral Equation and Operator Theory, 77, 109-121. https://doi.org/10.1007/s00020-013-2074-0
- 9. Liu, L. (2016) 2-Local Lie Derivations on Semi-Finite Factor von Neumann Algebras. Linear and Multilinear Algebra, 64, 1679-1686. https://doi.org/10.1080/03081087.2015.1112346
- 10. Halmos, P. (1982) A Hilbert Spaces Problem Book. 2th Edition, Spring-Verlag, New York.
https://doi.org/10.1007/978-1-4684-9330-6
- 11. Lu, F.Y. (2006) Lie Derivations of Certain CSL Algebras. Israel Journal of Mathematics, 155, 149-156.
https://doi.org/10.1007/BF02773953
- 12. Han, D.G. (1993) Additive Derivations of Nest Algebras. Proceedings of the American Society, 119, 1165-1169.
https://doi.org/10.1090/S0002-9939-1993-1186986-5
NOTES
*通讯作者。








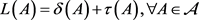 ,其中
,。类似于局部导子和2-局部导子,自然地可以定义局部Lie导子和2-局部Lie导子,文献 [8] 首次提出了局部Lie导子和2-局部Lie导子的概念,称线性映射
为局部Lie导子,若对
,存在依赖于A的Lie导子
使得
。映射(无线性或连续假设)
称为2-局部Lie导子,若对
,存在依赖于A,B的Lie导子
使得
,。相比于2-局部导子的研究,2-局部Lie导子的研究还相对较少,陆芳言教授 [8] 研究了维数大于2的Banach空间X上的有界线性算子全体构成的代数B(X)上的这两类映射,证明了2-局部Lie导子
具有形式
,其中
,。类似于局部导子和2-局部导子,自然地可以定义局部Lie导子和2-局部Lie导子,文献 [8] 首次提出了局部Lie导子和2-局部Lie导子的概念,称线性映射
为局部Lie导子,若对
,存在依赖于A的Lie导子
使得
。映射(无线性或连续假设)
称为2-局部Lie导子,若对
,存在依赖于A,B的Lie导子
使得
,。相比于2-局部导子的研究,2-局部Lie导子的研究还相对较少,陆芳言教授 [8] 研究了维数大于2的Banach空间X上的有界线性算子全体构成的代数B(X)上的这两类映射,证明了2-局部Lie导子
具有形式