 Journal of Water Resources Research 水资源研究, 2013, 2, 242-247 http://dx.doi.org/10.12677/jwrr.2013.24034 Published Online August 2013 (http://www.hanspub.org/journal/jwrr.html) Identification of Hydrologic Model Change-Point for Middle Yantgze River* Pan Liu1, Chao Deng1, Honggang Z hang2, Ya n S hen1, Shengxiang Ding2 1State Key Laboratory of Water Resources and Hydropower Engineering Science, Wuhan University, Wuhan 2Hydrology Bureau of Changjiang Water Resources Commission, Wuhan Email: liupan@whu.edu.cn Received: May 13th, 2013; revised: Jun. 7th, 2013; accepted: Jun. 21st, 2013 Abstract: It is very important to identify the model change-point for scientific understanding of the hydro- logic simulation. Based on the Bayesian change-point estimation of the general linear model, a method has been set up to identify the change-point of hydrologic systematic model, especially a multiple inputs—single output linear model. With the cases study of the middle Yangze River, two models have been set up to simu- late the flows from Yichang to Shashi and Luoshan stations, respectively. It is indicated that no significant change has taken place in the studied area. Keywords: Systematic Model; Change-Point of Model; Multiple Input Single Output; Bayesian 长江中游水文系统模型变异诊断研究* 刘 攀1,邓 超1,张洪刚 2,沈 艳1,丁胜祥 2 1武汉大学水资源与水电工程科学国家重点实验室,武汉 2长江水利委员会水文局,武汉 Email: liupan@whu.edu.cn 收稿日期:2013 年5月13 日;修回日期:2013 年6月7日;录用日期:2013 年6月21 日 摘 要:水文模型结构变异分析可为水文模拟提供科学依据。针对多输入单输出线性系统模型,基于 线性模型的贝叶斯变点估计方法,诊断和识别水文系统中的模型结构变异。以长江中游水文系统为研 究背景,分别建立了宜昌–沙市、宜昌–螺山两个多输入单输出线性系统模型,结果表明,长江中游 水文模型变异不显著,模拟中可作为一致性序列处理。 关键词:系统模型;模型变异;多输入单输出;贝叶斯 1. 引言 变化环境下的水文模拟是当今水文科学热点、难 点问题。受气候变化、人类活动影响,水文序列的平 稳性假定受到质疑和挑战。Merz 等指出,模型参数和 模型结构并不是一成不变的[1]。此时,如何识别模型 结构的时间变异点,并分析变异的物理成因,具有重 要的理论与实践意义。 多输入单输出线性系统模型将流域、河段或者水 库视为系统的输入或者输出单元,通过数学工具映射 输入输出之间的数学关系,是应用广泛的水文模型, 适应于成因复杂的水文水资源模拟[2,3]。本文基于多输 入单输出系统模型,采用线性模型的贝叶斯变点估计 方法,开展模型变异点诊断和识别研究。以长江中游 *基金项目:教育部新世纪优秀人才支持计划(NCET-11-0401);国 家自然科学基金项目(51190094;51249008)。 作者简介:刘攀(1978-),男(汉),湖南湘潭人,博士,武汉大学教 授,主要研究方向为:水文及水资源开发利用。 Copyright © 2013 Hanspub 242  刘攀,等:长江中游水文系统模型变异诊断研究 第2卷 · 第4期 为例,探讨模型结构变异问题。 2 线性模型的贝叶斯变点估计方法 多输入单输出线性系统模型可表述为[2,3]:设某一 输出时间序列可用多个输入的线性模型表示,写成矩 征阵形式为: yGb (1) 式中:y是一 N维向量,为自变量;G是一 N × M矩 阵,为因变量;b是线性模型的参数向量,ε是残差向 量;N为时间序列长度;M为输入变量个数。 在估计线性模型的变点位置时,可采用贝叶斯方 法[4-6]:由残差向量服从正态分布N (0, σ2)且独立,可 写出似然函数如下: T 2 2 2 2exp 2 N Lypyp yGb yGb (2) 式中: b ,, ,ω为变化点的位置。假定 b、 ω以及 logσ服从均匀分布,则可取 Φ的先验分布为: 1 p (3) 由贝叶斯公式 T 2 2 2 1 2exp 2 N pyLyp yGb yGb (4) 对参数 b和ε进行积分,最终可得到 ω的概率是 2 1 TTT T 12 T NM yy yGGGGy py GG (5) 为了计算标准化以后的任意一点可能是变点的 概率,可采用 1 j jN i i py py py (6) 在利用上面的通用模型进行变点分析的时候,可 通过构造不同的矩阵 G,用来分析不同的线性模型。 在多输入单输出系统模型中,如果模型在 ω点发 生变化,则: 1211 1211 , , ii mim i ii mim hxh xhxi yhxh xhxi (7) 为了应用上述变点模型,相应的可取(公式(9)见下): T 111 ,,,,,,, mm mm bhh hhh h 1 (8) T 12 ,,, N yyy y (10) 这样,可以采用式(5)和(6 )来推求系统模型的各点 发生变化的概率,取概率最大的为最终的模型变点估 计ω。贝叶斯方法对于变点位置发生在两端的情况, 需要分析合理性;并且理论上得到的变点位置,仍需 要从物理成因上进行分析其合理性。 3. 研究实例 选取长江中游干流的宜昌、沙市、螺山 3个控制 站、主要支流包括清江长阳站、沮漳河河榕站、荆南 三河——松滋河、虎渡河、藕池河控制站,以及洞庭 湖水系四水——湘江、资水、沅水和澧水控制站的实 测日平均流量资料,宜螺区间水系概化图如图 1所示。 采用算术平均得到宜昌–沙市区间、宜昌–螺山 区间的日平均降水量。宜昌–沙市区间的流量和降雨 资料序列为 1952 年1月1日~2010 年12 月31 日,沙 市站的观测流量资料序列为1991 年1月1日~2010 年 12 月31 日;宜昌–螺山区间的流量和降水资料的资 料序列为1955 年1月1日~2010 年12 月31 日,其中 12 1 23 2 1 T 23 34 12 00 0 00 0 00 0 00 0 00 0 00 0 m m mm mm Nm mm Nm N xx x xx x xx x Gxx x xx x xx x 1 2 (9) Copyright © 2013 Hanspub 243  刘攀,等:长江中游水文系统模型变异诊断研究 第2卷 · 第4期 三峡 清江 枝城 沮漳河 松滋口 太平口 藕池口 城陵矶 宜昌 螺山 长阳 澧水 沅江 资水 湘水 洞庭湖 河榕 沙市 Figure 1. The sketch of the Middle Yantgze River 潭站缺1987 年非汛期(1 月1日~4 月30日,11 月1 3.1. 宜昌–沙市水文模拟 3.1.1. 系统模型 河道通畅,流量、雨量资料齐全, 除干 考洪 3.1.2. 变异诊断 模型的贝叶斯变点估计方法,对宜 昌– 系统模型变异点概率分布如图 2所示。变异时间发生 模拟计算,参数识别 结果 5、 1996 Middle Yantgze River system- odels 表1. 长江中游系统模型精度评定 模型方案 2径流总量相对 误差 RE (%) 图1. 长江中游宜昌至螺山河段水系概化图 湘 日~12 月31 日)的流量数据。根据我国《水文情报预 报规范》(GB/T 22482-2008)[7],计算采用模型效率系 数R2 (确定性系数)和径流总量相对误差RE 进行精度 评定。 宜昌至沙市的 流流量以外,主要有清江 (控制站为长阳站)和沮 漳河(控制站为河榕站)两大支流汇入,如图 1所示, 区间面积约为 26532 km2。根据《长江流域洪水预报方 案汇编》,以 0.361 倍的长阳站流量作为河榕站的流量 过程,同时,多输入单输出模型要求各输出之间不能 存在自相关关系,因此将长阳、河榕合并为一个输入。 模型的输入序列包括宜昌站(实测)、长阳站 + 河榕站、 区间降雨(宜昌至沙市);输出为沙市站的径流过程。 采用最小二乘法识别脉冲响应函数,记忆长度参 水传播时间并采用试算法求得。模型率定期为 1991~2002 年,检验期为 2003~2010 年,各输入的记 忆长度分别为 2、2和3,对应的增益因子分别为 0.8713、0.6567 和0.0448。模型的评价结果如表1所 示,模型效率系数在率定期和检验期分别到达 98.42% 和97.89%以上,径流总量相对误差均不超过 5%。 采用上述线性 沙市系统模型进行变异性分析,得到宜昌–沙市 在1996 年5月24 日,与三峡大江截流时间 1997 年 11 月相对应,可能为变异点。 根据这一变异点,将 1991~2010 年的时间序列分 为两段,分别采用系统模型进行 如图 3所示。可以看出,经变异分割后,分割前后 的参数变化不大;进一步采用模型对沙市进行径流模 拟(表2),在增加变异点后,模拟确定性系数由 98.29% 提高到 98.33%,变化并不显著,由于无显著物理成因, 可认为宜昌–沙市系统模型无需考虑模型变异。 为进一步论证宜昌–沙市系统模型无变异的结 论,将 1991~2010 年数据分为4段:1991~199 ~2000、2001~2005 以及2006~2010,分别采用多 输入单输出线性系统模型率定参数,得到结果如图 4 所示。发现模型参数变异性不大,支持了宜昌–沙市 系统模型无变异的结论。 Table 1. The measurements for the atic m 时段 率系数R (%) 效 率定期 2002) (1991~98.42 −3.76 宜昌–沙市模型 检验期 97.89 −4.76 率定期(1955~1990) 99.20 −0.37 考虑“三口” 宜昌–螺山模型 检验期(1991~2010) 99.23 −0.13 率定期(1955~1990) 90.95 −3.33 宜昌–螺山模型 检验期(1991~2010) 92.02 −3.96 (2003~2010) 不考虑“三口” Copyright © 2013 Hanspub 244 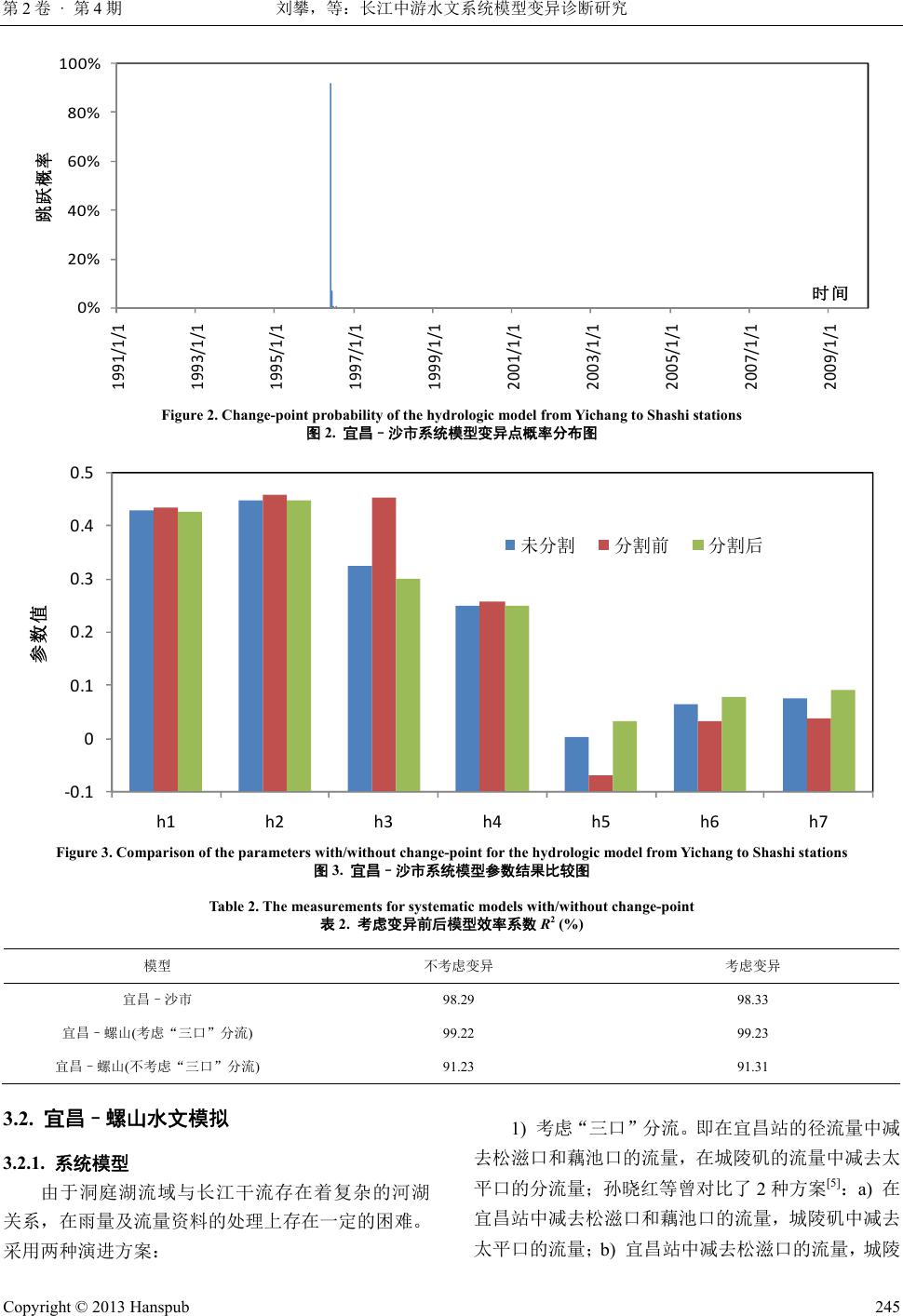 刘攀,等:长江中游水文系统模型变异诊断研究 第2卷 · 第4期 0% 20% 40% 60% 80% 100% 1991/1/1 1993/1/1 1995/1/1 1997/1/1 1999/1/1 2001/1/1 2003/1/1 2005/1/1 2007/1/1 2009/1/1 跳跃概率 时间 Figure 2. Change-point probability of the hydrologic model from Yichang to Shashi stations 图2. 宜昌–沙市系统模型变异点概率分布图 ‐0.1 0 0.1 0.2 0.3 0.4 0.5 h1 h2 h3 h4 h5 h6 h7 参数值 未分割 分割前 分割后 Figure 3. Comparison of the parameters with/without change-point for the hydrologic model from Yichang to Shashi stations 图3. 宜昌–沙市系统模型参数结果比较图 Table 2. The measurements for systematic models with/without change-point 模型 考虑变异 表2. 考虑变异前后模型效率系数 R2 (%) 不考虑变异 宜昌–沙市 98.33 98.29 宜昌–螺山(考虑“三口”分流) 宜昌–螺山 口”分流) 99.22 99.23 (不考虑“三 91.23 91.31 3.2. 宜昌–螺山水文模拟 .2.1. 系统模型 复杂的河湖 雨量及流量资料的处理上存在一定的困难。 演进方案: 1) 考虑“三口”分流。即在宜昌站的径流量中减 去松滋口和藕池口的流量,在城陵矶的流量中减去太 平口 站中减去松滋口的流量,城陵 3 由于洞庭湖流域与长江干流存在着 关系,在 采用两种 的分流量;孙晓红等曾对比了 2种方案[5]:a) 在 宜昌站中减去松滋口和藕池口的流量,城陵矶中减去 太平口的流量; b) 宜昌 Copyright © 2013 Hanspub 245  刘攀,等:长江中游水文系统模型变异诊断研究 第2卷 · 第4期 矶中 55~1990 年,检验期为 1991~ 2010 3.2.2 计方法,对宜昌~螺 异分析,得到考虑“三口”分流和 不考 模拟计算。如表 2所 示, 减去藕池口和太平口的流量。经过反复计算分析 比较,方案a)的精度优于方案 b),因此本文采用方案 a)。考虑洞庭湖“三口”分流的影响,各输入为:宜 昌1(宜昌–松滋口–藕池口)、长阳 + 河榕、城陵矶 1(城陵矶–太平口)、区间降雨(宜昌至螺山),输出为 螺山站的径流过程。 2) 不考虑“三口”分流。即将洞庭四水和湖区降 雨作为区间入流,当作模型的独立输入量。输入序列 包括宜昌、长阳 + 河榕、桃江、桃源、石门、湘潭、 区间降雨(宜昌至螺山),输出为螺山站的径流过程。 模型率定期为 19 年,结果见表 1和图 5。 . 变异诊断 同样采用线性模型的变点估 山系统模型开展变 虑“三口”分流两种情形下的变异点概率分布如 图6所示。变异时间分别发生在 2006 年4月18 日和 1959 年2月19 日,均无显著物理成因,且发生在序 列的两端,不考虑为变异点。 根据这一变异点,将 1955~2010 年的时间序列分 为两段,分别采用系统模型进行 在增加变异点后,模拟确定性系数变化并不显著, 为简单起见,可认为宜昌–螺山系统模型无需考虑模 型变异。 ‐0.2 ‐0.1 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 年 系数1系数2系数3系数4系数5系数6 系数值 1991‐1995 1996‐2000 2001‐2005 2006‐2010 系数7 Figure 4. Parameters with separated time periods for the hydrologic model from Yichang to Shashi stations 图4. 宜昌–沙市分段率定模型参数结果图 0 10000 20000 30000 40000 50000 60000 70000 80000 90000 1955-1-1 1958-1-1 1961-1-1 1964-1-1 1967-1-1 1970-1-1 1973-1-11976-1-1 1979-1-1 1982-1-1 1985-1-1 1988-1-1 流量(m³/s) 时间(年-月-日) 实测 考虑“三口” 不考虑“三口” (a) 0 10000 20000 30000 40000 50000 60000 70000 80000 90000 1991-1-1 1994-1-1 1997-1-1 2000-1-1 2003-1-1 2006-1-1 2009-1-1 流量(m³/s) 时间(年-月-日) 实测 考虑“三口” 不考虑“三口” (b) Figure 5. Comparison of observed and simulated flow hydrographs; (a) 1955-1990 years; (b) 1991-2010 years 图5. 宜昌至螺山区间模拟与实测过程;(a) 1955~1990年;(b) 1991~2010年 Copyright © 2013 Hanspub 246  刘攀,等:长江中游水文系统模型变异诊断研究 第2卷 · 第4期 0% 10% 20% 30% 40% 50% 60% 70% 80% 90% 100% /1/1 /1/1 /1/1 /1/1 /1/1 /1/1 /1/1 /1/1 /1/1 /1/1 /1/1 /1/1 /1/1 /1/1 /1/1 /1/1 /1/1 /1/1 跳跃点概率 不考虑"三口" 1955 1958 1961 1964 1967 1970 1973 1976 1979 1982 1985 1988 1991 1994 1997 2000 2003 2006 2009 /1/1 时间 考虑"三口" Figure 6. Probability of the change-point model from Yichang to Luoshan stations 图6. 宜昌–螺山系统模型变异点概率分布图 4. 结语 基于线性模型的贝叶斯变点估计方法,诊断线性 系统模型变异,提出了识别水文系统中模型结构变异 的方法。以长江中游水文系统为研究背景,分别建立 了宜昌–沙市、宜昌–螺山多输入单输出线性系统模 型,结果表明,长江中游水文模型变异不显著,模拟 中可作为一致性序列处理。 考文献 (References) MERZ, R., PARAJKA, J. and BLOÖSCHL, G. Time stability of Guiya. Flood simulation study in the Dongtinghu and Yichang- Hankou basins of the Yangtze River. International Journal Hy- droelectric Energy, 2001, 19(3): 46-48. [3] 沈艳, 刘攀, 刘玥. 三峡水库调蓄后长江中游径流演变趋势 分析[J]. 人民长江, 2013, 44(4): 25-27. SHEN Yan, LIU Pan and LIU Yue. Analysis on runoff evolution trend of middle Yangtze River after impoundment of Three Gorges Reservoir. Yangtze River, 2013, 44(4): 25-27. [4] RASMUSSEN, P. Bayesian estimation of change points using the general linear model. Water Resources Research, 2001, 37 (11): 2723-2731. [5] SEIDOU, O., ASSELIN, J. J. and OUARDA, T. B. M. J. Bayes- ian multivariate linear regression o change al variables. Water Resources ., SEIDOU, O., OUARDA, T. B. M. J. and 参 [1] catchment model parameters: Implications for climate impact analyses. Water Resources Research, 2011, 47(2): W02531. [2] 孙晓红, 郭生练, 郭海晋, 徐高洪, 陈桂亚. 长江洞庭湖和宜 昌至汉口流域洪水过程模拟研究[J]. 水电能源科学, 2001, 19(3): 46-48. SUN Xiaohong, GUO Shenglian, GUO Haijing and CHEN [7] with application t point models in hydrometeorologic , 43(8). Research, 2007 [6] BEAULIEU, C ZHANG, X. Intercomparison of homogenization techniques for precipitation data continued: Comparison of two recent Bayesian change point models. Water Resources Research, 2009, 45(8): 水 GB/T 22482-2008, 文情报预报规范[S]. 北京: 中国标准出 版社, 2009. GB/T 22482-2008, The hydrological forecasting standard. Bei- jing: China Standard Press, 2009. Copyright © 2013 Hanspub 247 |