 Pure Mathematics 理论数学, 2013, 3, 354-361 http://dx.doi.org/10.12677/pm.2013.36054 Published Online November 2013 (http://www.hanspub.org/journal/pm.html) A New Alternating Segment Explicit-Implicit Scheme for One Dimensional Convection-Diffusion Equation Haiming Gu, Qian Liu Qingdao University of Science and Technology, Qingdao Email: guhm@ns.qd.sd.cn Received: Sep. 10th, 2013; revised: Sep. 24th, 2013; accepted: Sep. 27th, 2013 Copyright © 2013 Haiming Gu, Qian Liu. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. Abstract: A new alternating segment explicit-implicit scheme for convection-diffusion equation was given and this scheme was proved to be unconditionally stable. This scheme can be used in parallel computation and the spatial accuracy rate is . A numerical experiment shows that this scheme has high accuracy and quick ratio of convergence. 4 Oh Keywords: Convection-Diffusion Equation; Finite Difference; Parallel Algorithm; Absolute Stability 一维对流扩散方程的新交替分段显隐格式 顾海明,刘 倩 青岛科技大学,青岛 Email: guhm@ns.qd.sd.cn 收稿日期:2013 年9月10日;修回日期:2013 年9月24 日;录用日期:2013年9月27 日 摘 要:对一维对流扩散方程给出了一组新的交替分段显隐格式,并证明了格式无条件稳定。它可以 用于并行算法且精度可以达到 阶。数值实验表明,此格式具有精度高,收敛快的特点。 4 Oh 关键词:对流扩散方程;有限差分;并行计算;绝对稳定 1. 引言 对流扩散方程是描述流体运动 某些物理现象的一 类重要的偏微分方程, 在热传导、渗流力 学与粒子扩散 等 方面有重要应用[1],因此研究其数值计算方法有重要的现实意义,开展并行差分法的研究也已成为偏微分方程 数值分析的重要内容之一。在有限差分格式的并行计算研究中,D. J. Evans中提出了求解对流扩散方程的交替 分组格式[2],随后也出现了新的算法[3-5],但是这些算法的精度几乎是 2 Oh 阶的。本文在给出差分格式的基础 上构造了交替显隐分段格式,且精度可达到 4 Oh 阶,并分析了格式的稳定性,最后给出算例得到证实。 2. 差分格式 考虑一维对流扩散方程: 2 2,0,0, 0 uu u ab xltTb txx (1) Open Access 354  顾海明,刘倩 一维对流扩散方程的新交替分段显隐格式 0,,, 0utult tT 0 ,0 ,0uxu xx l 建立它的交替分段显隐格式。 首先对区域进行等距剖分,令 h和 分别为空间和时间步长。设精确解为,定义 为精确解 ,uxt n i U ,n in i uxt u的数值近似解, 1 i x ih , ; 1, 2,,1iJnn , 0,1, ,nT 。特别的,本文讨论 l h J 的问题的交替显隐格式,其中为一整数。 24,JKL L 1 由泰勒展开我们能得到截断误差为 的显格式(2)和隐格式(2 ): 4 h 1 22 1 1308 168 16 nnnn n iiii i UbrUarh brUarhbrUarhbrUarhbrU 1 n i (2) 1111 22 1 1308 168 16 nnnn iiii br Uarhbr UarhbrUarhbr Uarhbr UU 1 1 nn ii (3) 其中: 2 12 rh 。 在此基础上,我们可以得到逼近方程(1)的如下四个非对称差分格式: 111 12 21 174 2 82123 42 nnn iii nnn iii br UrbahUrbahU rbahUrb ahUbrUrb ahU 1 n i (4) 11 1 11 21 42 12382 42 17 nn n ii i nnn iii rahbUbrUrb ahUrbahU rbahUrbah UbrU 1 2 n i (5) 111 21 12 82 12342 174 2 nnn iii nnn iii rbahUrahbUbr UrbahU rUrahbUrb ahU 1 1 n i (6) 111 21 11 42 17 4212382 nnn iii nn n ii i rbahUrbahUbr U rbahUbr Urbah UrbahU 2 n i (7) 3. 新交替分段显隐格式 3.1. 新格式 对于 42 J KL,在奇数时间层上, J 个网络节点按从左至右的空间分为 2段,并按“显式段,隐式 段,…,显式段,隐式段”来构造差分格式。其中显式段包含 个点,每个点上均采用式(2)计算,所以各点可 以单独的显式求解。隐式段包含 个点,采用式(4),(5),(3)…(3),(6),(7),本段只能通过求解线性方程组 进行求值。而在偶数时间层上,显式段包含 个点,每个点上均采用式(2)计算,靠近边界的两个隐式段分别包 括个点和 2个点,分别用(3)…(3),(6),(7)和(4 ),(5)计算。从而偶数时间层上的分段情况为:“隐式段, 显式段,…,隐式段,显式段,隐式段”。用线性方程组的形式表示如下: K L 4L L 2L n为偶数时,对 层上的隐式段节点1n 1 ,n j x t;1,,4 2jiL i L ; 42,0,1, ,1iLkkK , 有如下的求解格式: 111 123 11 174 2 82123 42 nnn iLiL iL nnn iLiL iLiL brUrb ahUrb ahU rbahUrbah UbrUrbahU 2 n (8) 11 1 12 3 12 42123 82 42 17 nn n iLiLiL iL nnn iLiL iL rbahUbrUrbahU rbahU rbah Urbah UbrU 1 4 n (9) Open Access 355 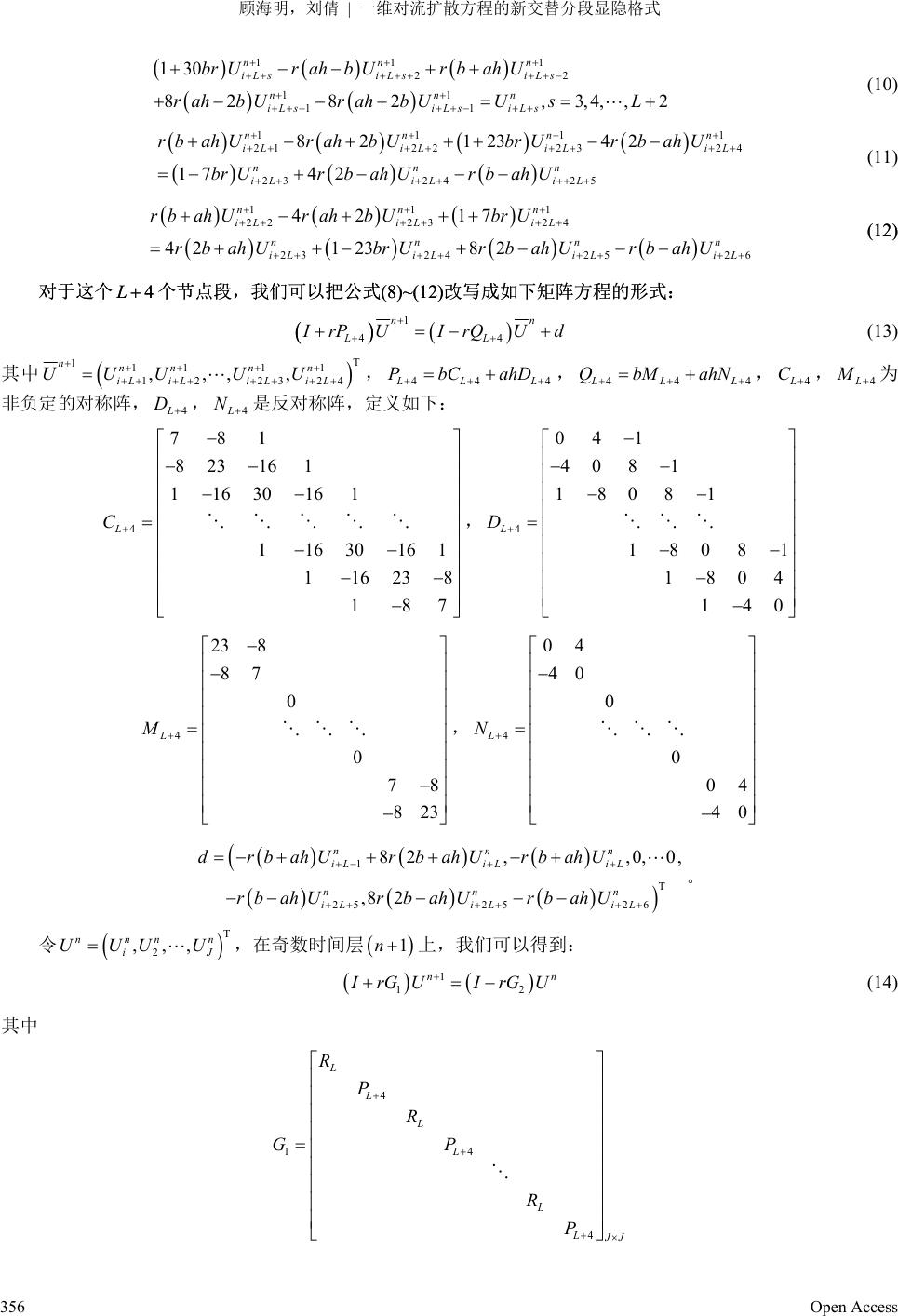 顾海明,刘倩 一维对流扩散方程的新交替分段显隐格式 11 1 22 11 11 130 82 82,3,4,, nn n iLs iLsiLs nnn iLsiLs iLs brUrahbUrbahU rah bUrah bUUsL 2 (10) 111 2122 2324 2324 25 82 12342 1742 nnn iLiL iLiL nnn iLiLi L rbahUrahbUbr UrbahU brUrbah UrbahU 1n (11) 111 2223 24 232425 26 42 17 4212382 nnn iLiLiL nn n iLiLiL iL rbahUrahbUbrU rbahUbrUrbahUrbahU n (12) (12) 对于这个 个节点段,我们可以把公式(8)~(12)改写成如下矩阵方程的形式: 对于这个个节点段,我们可以把公式(8)~(12)改写成如下矩阵方程的形式: 4L4L 1 44 n LL n I rPUI rQUd (13) 其中 T 1111 1 12 2324 ,,, , nnnn n iL iLiLiL UUU UU ,444LL P bCahDL ,444LL Q bMahNL ,4,4LL C M 为 非负定的对称阵, 4L,4L D N 是反对称阵,定义如下: 4 781 82316 1 11630161 11630161 116238 187 L C ,4 04 1 40 81 1808 1 18081 1804 140 L D 4 23 8 87 0 0 78 823 L M ,4 04 40 0 0 04 40 L N 1 T 2525 26 82,,0, 0, ,8 2 nnn iLiLiL nnn iLiL iL d rbahUrbahUrbahU rb ahUrb ahUrbahU T 。 令 ,在奇数时间层 2 ,,, nnn n i UUU U J 1n 上,我们可以得到: 1 1 n 2 n I rG UIrGU (14) 其中 4 14 4 L L L L L L J J R P R GP R P Open Access 356  顾海明,刘倩 一维对流扩散方程的新交替分段显隐格式 其中 L R为 L L的零矩阵。 44 2 T LL L PP bC 4 ,而 4L C 为非负定的对称阵且,则是非负定的。 0b11 T GG 2 4 2 2 L L L L J J A R P G R Y 其中 ,容易得出矩阵 2 78 04 823 40 Yb ah 78 82 3 是非负定的。 22LL AbVahW 2L2L V 为非负定的对称阵, 2L W 是一个反对称阵,定义如下: 2 3016 1 16 30161 11630161 11630161 116238 187 L V ,2 08 1 80 81 18081 18081 1404 140 L W 而 因此0b22 2 T LL L2 A AbV 是非负定矩阵,同理 22 T YY 也是非负定矩阵。又有 L R为零矩阵, 44 T LL PP 是 非负定的,则是非负定的。 22 T GG 对于偶数时间层,可以得到如下矩阵方程: 2n 2 2 n IrGU IrGU 1 1 n (15) 从而对于可以得到如下完整格式: 0, 2, 4,,n 1 12 2 21 nn n IrGU IrGU IrGU IrGU 1n (16) 3.2. 稳定性分析 Kellogg 引理 设0 , T CC是非负定的,则 1 I C 必存在且: 11 2 1 2 1 IC IC IC (17) 由式(16)可以得到 。 2nn UGU 其中 ,记 11 211 GIrGIrGIrG IrG 2 1 2 GI rGGI rG 2 ,又有 , 是非 负定矩阵,由引理可知: 11 T GG2 T GG2 1 2 1,1, 2 ii IrG IrGi 于是 21GGG ,因此该格式是无条件稳定的。 3.3. 截断误差 下面讨论格式的误差。令为算子的离散形式,所以有: 2 h L L Open Access 357  顾海明,刘倩 一维对流扩散方程的新交替分段显隐格式 21 22 1 25 5 22 36 11308 16816 112 1248 2! 5! nnn nnnn hi iiiiii n nn nn tttx xx ii iii Luubr ubrarhuarhbruarhbr uarhbru h uuarh ubrh uarhuoh 1 (18) 相应的截断误差为: 46 25 2 4 2! 5! n n n n hi tt iii h Lu Luua uo h (19) 类似可得其它格式的截断误差形式如下: 26 322 12 24 2!2! 2! nnn n n n h ittttxttxxt iii ii hh LuLuuarh uubruoh 2 (20) 4 26 22 313 26 2! 2! 42! nn n n n hitttxt xtt ii ii n xxt i LuLuarhuarhurahbhuu hh br uoh n i (21) 5 26 22 313 106 2! 2! 20 2! nnn n n hitttxt xtt iii i n xxt i LuLuarhuarhuarhbrhuu hh br uoh n i (22) 6 26 22 313 106 2! 2! 20 2! nn n n n hitttxt xtt iii i n xxt i LuLuarh uarhuarhbrhuu hh br uoh n i (23) 7 26 22 313 26 2! 2! 42! nn n n n hitttxt xtt ii ii n xxt i LuLuarh uarhuarhbrhuu hh br uoh n i (24) 在本格式中,(4)和(6)在两层的节点 s x ,其中 1, 23siLi L ; 42 , 0,1,1iLkk K 处是交替使 用的,同样式(5)和(7)在 也是交替使用的;其它的点处是(2)和(3)交替使用。采用这 6个格 式的节点,我们比较如下的三组式子:一组是式(4)在点 2, 4siL i 2L 1 , in x t的Taylor展开式和式(6)在 1 , in x t的截断误差 式,另一组是式(5)在点 1 , in x t的Taylor 展开式和式(7)在 1 , in x t的截断误差式,最后一组是式(2)在点 1 , in x t 的Taylor展开式和式(3)在 1 , in x t的截断误差式: 11 1 1 412 26 122 313 106 2! 2! 20 2! nn n n n hitttxt xtt iii i n xxt i LuLuarhuarhuarhbr huu hh br uoh 1n i (25) 11 1 1 512 26 122 313 26 2! 2! 42! nn n n n hitttxt xtt iii i n xxt i LuLuarhuarhuarhbr huu hh br uoh 1n i (26) Open Access 358  顾海明,刘倩 一维对流扩散方程的新交替分段显隐格式 11 1 212 2 122 12 2! 2! 24 2! nn n n hittxt xtt iii n xxt i LuLuuarh uu hh br uoh 1 6 n i (27) 式(25)和式(23)中的第一项与第四项符号相反,第二项与第三项部分可以抵消;从而这两个格式在两层交替 用计算时误差会抵消一部分。同样的结果对式(26)和式(24)以及 式(27 )和式(20)也成立。 类似可以得到,对于每一个隐式段的最后两个以及隐格式节点,对应于式(6),式(7)和式(3)相应点 1 , in x t处 的Taylor展开式,可以得到如下截断误差: 111 1 612 26 122 313 26 2! 2! 42! nn n n n hitttxt xtt iii i n xxt i LuLuarhuarhuarhbr huu hh br uoh 1n i (28) 11 1 1 712 26 122 313 106 2! 2! 20 2! nnn n n hitttxtxtt iiii n xxt i LuLuarhuarhuarhbr huu hh br uoh 1n i (29) 46 1 1 1 35 12 4 2! 5! n n n n hi tt ii i h LuLuua uo h (30) 可以看到,式(28)和式(23)中的第一项和第四项符号相反,第二项和第三项可以抵消一部分,抵消之后的两 层可以达到 Oh 。式(29)和式(22)有同样的结果成立,所以本格式的整体截断误差可以达到 Oh 。 4. 数值实验 我们用下例做数值实验 2 2,0 ,0 uu u x lt txx T 0,1,, 0utut tT ,0cos 2π,0uxxx l 精确解为 2 4π ,ecos2π,0 1 t uxtx tx 令1 h J ,2 h ,计算时间为Tn 的解。其中 为精确解 n i U ,n in i uxt u 的数值近似解, 1 i x ih , 1, 2,1iJ;nn ,误差的模和模度量范数定义如下: 2 L L 1 2 2 2, 21 ,, J nn n xi iniin i EU uxtU uxth ,1 ,max, nn n xi ini in iJ EU uxtU uxt 方法的收敛率定义如下: Open Access 359 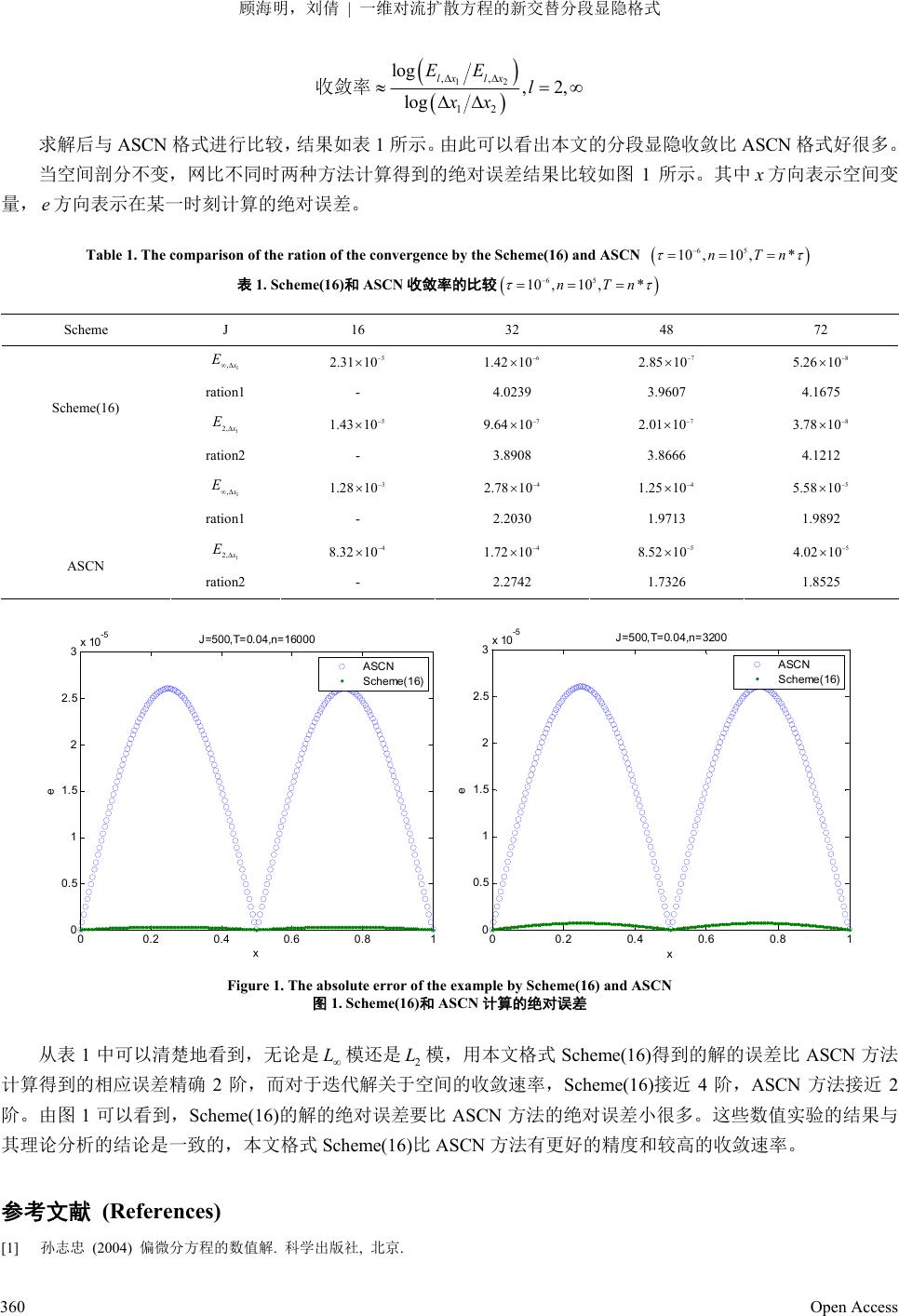 顾海明,刘倩 一维对流扩散方程的新交替分段显隐格式 12 ,, 12 log ,2, log lxlx EE l xx 收敛率 求解后与ASCN 格式进行比较,结果如表 1所示。由此可以看出本文的分段显隐收敛比 ASCN 格式好很多。 当空间剖分不变,网比不同时两种方法计算得到的绝对误差结果比较如图 1所示。其中 x 方向表示空间变 量,方向表示在某一时刻计算的绝对误差。 e Table 1. The comparison of the ration of the convergence by the Scheme(16) and ASCN 65 10,10,*nTn 表1. Scheme(16)和ASCN收敛率的比较 65 10,10 ,*nTn Scheme J 16 32 48 72 1 , x E 5 2.31 10 6 1.4210 7 2.85 10 8 5.2610 ration1 - 4.0239 3.9607 4.1675 1 2, x E 5 1.43 10 7 9.64 10 7 2.01 10 8 3.78 10 Scheme(16) ration2 - 3.8908 3.8666 4.1212 1 , x E 3 1.28 10 4 2.78 10 4 1.25 10 5 5.58 10 ration1 - 2.2030 1.9713 1.9892 1 2, x E 4 8.3210 4 1.7210 5 8.5210 5 4.02 10 ASCN ration2 - 2.2742 1.7326 1.8525 00.20.4 0.6 0.81 0 0.5 1 1.5 2 2.5 3x 10 -5 x e J=500,T=0.04,n=16000 ASCN Scheme( 16) 00.2 0.4 0.60.8 1 0 0.5 1 1.5 2 2.5 3x 10 -5 x e J=500,T=0.04,n=3200 ASCN Scheme(16) Figure 1. The absolute error of the example by Scheme(16) and ASCN 图1. Scheme(16)和ASCN计算的绝对误差 从表 1中可以清楚地看到,无论是模还是模,用本文格式 Scheme(16)得到的解的误差比 ASCN方法 计算得到的相应误差精确2阶,而对于迭代解关于空间的收敛速率,Scheme(16)接近 4阶,ASCN 方法接近 2 阶。由图 1可以看到,Scheme(16)的解的绝对误差要比 ASCN方法的绝对误差小很多。这些数值实验的结果与 其理论分析的结论是一致的,本文格式Scheme(16)比ASCN 方法有更好的精度和较高的收敛速率。 L2 L 参考文献 (References) [1] 孙志忠 (2004) 偏微分方程的数值解. 科学出版社, 北京. Open Access 360  顾海明,刘倩 一维对流扩散方程的新交替分段显隐格式 Open Access 361 [2] Evans, D.J. (1985) Alternating group explicit method for the diffusion equations. Applied Mathematical Modelling, 9, 201-206. [3] 王文洽 (2002) 对流–扩散方程的一类交替分组方法. 高等学校计算数学学报 , 4, 289-297. [4] 左进明, 张天德 (2010) 五阶色散 KdV 方程的交替分段显–隐差分格式. 山东大学学报 ( 理学版 ), 10, 116-121. [5] 张守慧, 王文洽 (2007) 抛物型方程的 4 ()Oh精度新交替分段显隐格式. 山东大学学报 ( 理学版 ), 12, 1-7. |