Pure Mathematics
Vol.07 No.04(2017), Article ID:21382,4
pages
10.12677/PM.2017.74039
On the Finite p-Group with a Small Central Quotient
Xing Wu, Yulong Ma, Hailin Liu*
School of Mathematics and Statistics, Yunnan University, Kunming Yunnan
Received: Jun. 23rd, 2017; accepted: Jul. 8th, 2017; published: Jul. 17th, 2017

ABSTRACT
Let G be a finite noncyclic p-group of order greater than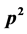 . If
. If 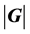 divides
divides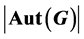 , then G is called a LA-group. The purpose of this paper was to consider the class of p-group
, then G is called a LA-group. The purpose of this paper was to consider the class of p-group 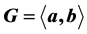 such that
such that 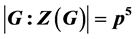 with the prime
with the prime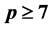 . We showed that such group G is LA-group.
. We showed that such group G is LA-group.
Keywords:Finite p-Group, LA-Group, Automorphism Group

具有小中心商的有限p-群
伍星,马玉龙,刘海林*
云南大学数学与统计学院,云南 昆明

收稿日期:2017年6月23日;录用日期:2017年7月8日;发布日期:2017年7月17日

摘 要
假设G是一个有限非交换p-群,并且G的阶大于 ,如果
,如果 整除
整除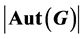 ,那么称G为LA-群。本文考虑了二元生成的有限p-群
,那么称G为LA-群。本文考虑了二元生成的有限p-群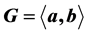 ,并且满足
,并且满足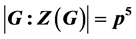 ,其中素数
,其中素数 。我们证明了这样的有限p-群是LA-群。
。我们证明了这样的有限p-群是LA-群。
关键词 :有限p-群,LA-群,自同构群

Copyright © 2017 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
设 是一个,
是一个,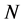 是
是 的正规子群。在本文中我们用
的正规子群。在本文中我们用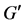 ,
, ,
, 和
和 分别表示群
分别表示群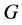 的导群,自同构群,中心和商群。用
的导群,自同构群,中心和商群。用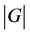 表示群
表示群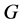 的阶。
的阶。
假设群 是一个有限非循环p-群,并且
是一个有限非循环p-群,并且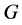 的阶大于
的阶大于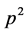 ,如果
,如果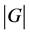 整除
整除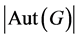 ,那么我们称这个p-群
,那么我们称这个p-群 为LA-群。对LA-群的研究有很久的历史。下面我们列出一些关于LA-群的一些结果:假设
为LA-群。对LA-群的研究有很久的历史。下面我们列出一些关于LA-群的一些结果:假设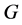 是一个阶
是一个阶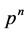 的有限非循环p-群,并且
的有限非循环p-群,并且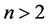 。如果
。如果 满足下列条件之一,那么
满足下列条件之一,那么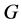 是LA-群。
是LA-群。
1) 是一个PN-群
是一个PN-群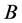 和一个交换群
和一个交换群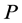 的直积,并且
的直积,并且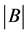 整除
整除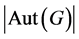 (见 [1] );
(见 [1] );
2)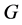 是p-交换p-群(见 [2] );
是p-交换p-群(见 [2] );
3) ,并且
,并且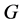 是亚循环的(见 [3] );
是亚循环的(见 [3] );
4) 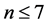 (见 [4] [5] );
(见 [4] [5] );
5)  (见 [6] );
(见 [6] );
6) ,并且
,并且 是有限的模p-群(见 [7] );
是有限的模p-群(见 [7] );
7) Frattini子群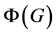 循环(见 [8] );
循环(见 [8] );
8)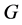 是一个指数为
是一个指数为 的循环子群(见 [9] );
的循环子群(见 [9] );
9)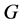 是一个极大类p-群(见 [1] );
是一个极大类p-群(见 [1] );
10) 对任意的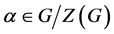 ,
, (见 [10] );
(见 [10] );
11)  (见 [11] );
(见 [11] );
12)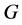 是余类为2的p-群(见 [12] )。
是余类为2的p-群(见 [12] )。
此外,在文献 [13] 中,作者刻画了满足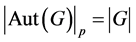 的极大类p-群
的极大类p-群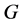 ,其中
,其中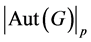 表示
表示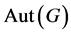 的Sylow-p子群的阶。再者满足
的Sylow-p子群的阶。再者满足 的p-群
的p-群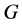 在文献 [14] 中被分类。
在文献 [14] 中被分类。
本文我们将LA-群推广到一类p-群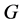 上:满足
上:满足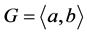 ,
,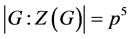 ,其中
,其中 为素数。现在我们陈述本文的主要结果。
为素数。现在我们陈述本文的主要结果。
定理1.1. 假设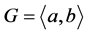 是一个阶大于等于
是一个阶大于等于 的有限非循环p-群,
的有限非循环p-群, 为素数,并且满足
为素数,并且满足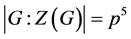 ,则
,则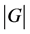 整除
整除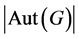 ,即
,即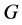 为LA-群。
为LA-群。
注1.1. 由引理2.1,我们可以假设群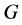 的幂零类
的幂零类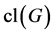 大于2。进一步,由文献 和 ,我们可以假设
大于2。进一步,由文献 和 ,我们可以假设 不是p-交换的,并且
不是p-交换的,并且 。
。
2. 预备引理
在本小节,我们将给出一些必要的预备结果。
首先,我们给出两个关于LA-群的结果,见文献 [15] [16] 。
引理2.1. ( [16] , THEOREM])假设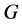 是一个有限非交换p-群,幂零类
是一个有限非交换p-群,幂零类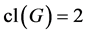 ,则
,则 的阶整除于
的阶整除于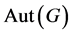 的阶。
的阶。
引理2.2. ( [15] , THEOREM])假设 是一个有限p-群
是一个有限p-群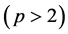 ,并且满足
,并且满足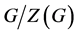 是一个非平凡的亚循环,则
是一个非平凡的亚循环,则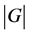 整除
整除 。
。
接下来的引理给出了有限亚循环p-群的判别准则。
引理2.3. ( [17] , K.III, S.11.4])假设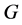 是一个有限p-群
是一个有限p-群 ,则
,则 是亚循环的当且仅当
是亚循环的当且仅当 ,其中
,其中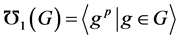 。
。
最后我们给出有限p-群正则的判别准则。
引理2.4. 假设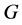 是一个有限p-群,
是一个有限p-群,
1) 如果 ,那么
,那么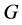 正则;
正则;
2) 如果 ,那么
,那么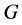 正则;
正则;
3) 如果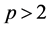 ,并且
,并且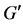 循环,那么
循环,那么 正则;
正则;
4) 如果 ,那么
,那么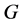 正则。
正则。
3. 定理证明
首先,我们考虑正则的情形: 是一个正则p-群,其中素数p没有限制。
是一个正则p-群,其中素数p没有限制。
引理3.1. 假设 是一有限非循环p-群,满足
是一有限非循环p-群,满足 ,则
,则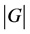 整除
整除 。
。
证明:假设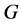 是一个正则p-群。注意到正则2-群是交换的,因此
是一个正则p-群。注意到正则2-群是交换的,因此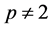 。因为
。因为 不是p-交换的,所以我们有
不是p-交换的,所以我们有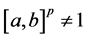 。又因为
。又因为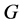 正则,所以
正则,所以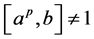 ,
, 。因此
。因此 并且
并且 。接下来我们有:
。接下来我们有: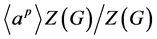 和
和 的交非平凡。事实,如果假设
的交非平凡。事实,如果假设 ,那么存在
,那么存在 满足
满足 ,因此
,因此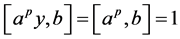 ,与前面的事实矛盾。若假设
,与前面的事实矛盾。若假设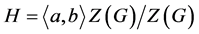 ,则很容易可得
,则很容易可得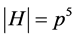 并且
并且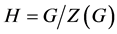 。进一步,由前面的事实可得
。进一步,由前面的事实可得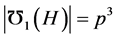 ,所以
,所以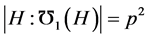 。从而由引理2.3,我们可得
。从而由引理2.3,我们可得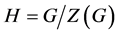 是亚循环的。因此由引理2.2,定理得证。
是亚循环的。因此由引理2.2,定理得证。
即使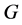 是一个非正则p-群,
是一个非正则p-群,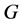 也是亚循环的。
也是亚循环的。
命题3.2. 假设 是一个阶大于等于
是一个阶大于等于 的有限非循环p-群,并且满足
的有限非循环p-群,并且满足
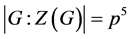 ,
, ,则
,则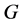 是亚交换的。
是亚交换的。
证明:由前面的讨论我们可知 具有下面的子群链:
具有下面的子群链: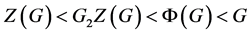 。因此我们有
。因此我们有 或者
或者 。如果
。如果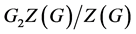 是p阶的循环群,那么
是p阶的循环群,那么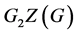 交换,所以
交换,所以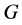 是亚交换的;接下来,假设
是亚交换的;接下来,假设 其中
其中 。如果
。如果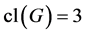 ,由文献( [17] , K.III, H.2.11, b]),那么我们可以在
,由文献( [17] , K.III, H.2.11, b]),那么我们可以在 中选择
中选择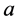 和
和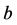 满足
满足 在
在 中,如果
中,如果 ,那么可以在
,那么可以在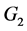 中选择
中选择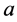 ,在
,在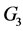 中选择
中选择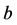 满足
满足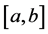 属于
属于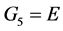 ;最后,如果
;最后,如果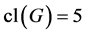 ,你们可以在
,你们可以在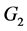 中选择
中选择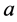 ,在
,在 中选择
中选择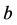 满足
满足 属于
属于 。因为
。因为 ,所以
,所以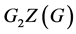 是交换的,因此
是交换的,因此 是亚交换的。
是亚交换的。
定理1.1的证明。注意到 的幂零类
的幂零类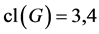 或者5。由于
或者5。由于 ,所以
,所以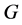 是正则的。因此由引理3.1可得定理1.1对所以的素数
是正则的。因此由引理3.1可得定理1.1对所以的素数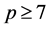 均成立。
均成立。
定理1. 的证明已完成,接下来我们给出一个推论。
推论3.3. 假设 是一个有限非循环p-群,满足
是一个有限非循环p-群,满足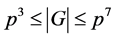 并且
并且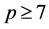 ,则
,则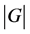 整除
整除 。
。
证明:注意到 ,所以
,所以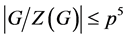 。由定理1.1和文献 ,推论得证。
。由定理1.1和文献 ,推论得证。
本文中,我们仅仅只考虑了这种情形: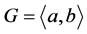 ,其中
,其中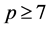 。但是由引理3.1,我们可知定理1.1对这种情况也是成立的:
。但是由引理3.1,我们可知定理1.1对这种情况也是成立的: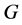 是正则的p-群,其中对素数p没有限制。因此,自然地我们有下面可以考虑的问题。
是正则的p-群,其中对素数p没有限制。因此,自然地我们有下面可以考虑的问题。
问题:定理1.1对这种情形是否成立: 是一个非正则的2-群,非正则3-群或者非正则5-群。对于这个问题我们也在进一步研究。我们可以预见到这种情形的复杂性。这将是一个巨大的工作。
是一个非正则的2-群,非正则3-群或者非正则5-群。对于这个问题我们也在进一步研究。我们可以预见到这种情形的复杂性。这将是一个巨大的工作。
基金项目
国家自然科学基金(11301468)、云南省自然科学基金(2013FB001)和云南大学第八届研究生科研创新项目资助(ynuy201688)。
文章引用
伍 星,马玉龙,刘海林. 具有小中心商的有限p-群
On the Finite p-Group with a Small Central Quotient[J]. 理论数学, 2017, 07(04): 297-300. http://dx.doi.org/10.12677/PM.2017.74039
参考文献 (References)
- 1. Otto, A. (1966) Central Automorphisms of a Finite P-Group. Duke Math, 125, 280-287.
- 2. Davitt, R.M. (1972) The Automorphism Group of Finite P-Abelian P-Groups Ill. Journal of Mathematics, 16, 76-85.
- 3. Davitt, R.M. (1970) The Automorphism Group of a Finite Metacyclic P-Group. Proceedings of the American Mathematical Society, 25, 876-879. https://doi.org/10.2307/2036770
- 4. Exarchakos, T. (1989) On P-Group of Small Order. Publications de l'Institut Mathématique, 45, 73-76.
- 5. Gavioli, N. (1993) The Number of Automorphisms of Groups of Order p^7. Proceedings of the Royal Irish Academy Section, A2, 177-184.
- 6. Flynm, J., Machale, D. and O'Brien, E.A. (1994) Finite Groups Whose Automorphism Groups Are 2-Group. Proceedings of the Royal Irish Academy Section, A2, 137-145.
- 7. Davitt, R.M. and Otto, A. (1972) On the Automorphism Group of a Finite Modular P-Group. Proceedings of the American Mathematical Society, 35, 399-404.
- 8. Fouladi, S., Jamali, A.R. and Orfi, R. (2008) On the Automorphism Group of a Finite P-Group with Cyclic Frattinisubgroup. Proceedings of the Royal Irish Academy, 108 A2, 165-175.
- 9. Xiao, C.C. (1990) A Conjecture on the Automorphism Group of a Finite P-Group. Rendiconti del Circolo Matematico di Palermo, 2, 347-351.
- 10. Yadav, M.K. (2007) On Automorphisms of Finite P-Groups. Journal of Group Theory, 10, 859-866. https://doi.org/10.1515/jgt.2007.064
- 11. Davitt, R.M. (1980) On the Automorphism Group of a Finite P-Group with a Small Central Quotient. Canadian Mathematical Society, 5, 1168-1176. https://doi.org/10.4153/CJM-1980-088-3
- 12. Fouladi, S., Jamali, A.R. and Orfi, R. (2007) Automorphism Groups of Finite P-Groups of Co-Class 2. Journal of Group Theory, 10, 437-440. https://doi.org/10.1515/jgt.2007.036
- 13. Malinowska, I. (2001) Finite P-Groups with Few P-Automorphisms. Journal of Group Theory, 4, 395-400. https://doi.org/10.1515/jgth.2001.029
- 14. Attar, M.S. (2015) On Equality of Order of a Finite P-Group and Order of Its Automorphism Group. Bulletin of the Malaysian Mathematical Sciences Society, 38, 461-466. https://doi.org/10.1007/s40840-014-0030-z
- 15. Davitt, R.M. and Otto, A.D. (1971) On the Automorphism Group of a Finite P-Group with the Central Quotient Metacyclic. Proceedings of the American Mathematical Society, 30, 467-472. https://doi.org/10.2307/2037717
- 16. Faudree, R. (1968) A Note on the Automorphism Group of a Group. Proceedings of the American Mathematical Society, 19, 1379-1382.
- 17. Huppert, B. and Endliche Gruppen, I. (1967) Die Grundlehren der math. Wissenschaften, Band 134. Springer-Verlag, Berlin and New York.
NOTES
*通讯作者。