Pure Mathematics
Vol.
09
No.
01
(
2019
), Article ID:
28662
,
13
pages
10.12677/PM.2019.91013
The Random-Effect Model of Bivariate Meta-Analysis Based on the Difference Mean
Pengfei Guo1,2,3, Shuangyin Liu2,3,4, Gang Li5*, Lei Zhang2,3,4,, Liang Cao2,3,4, Xiangru Sun6, Longqin Xu2,3,4
1College of Computational Science, Zhongkai University of Agriculture and Engineering, Guangzhou Guangdong
2Intelligent Agriculture Engineering Research Center of Guangdong Higher Education Institutes, Zhongkai University of Agriculture and Engineering, Guangzhou Guangdong
3Guangdong Province Key Laboratory of Waterfowl Healthy Breeding, Zhongkai University of Agriculture and Engineering, Guangzhou Guangdong
4College of Information Science and Technology, Zhongkai University of Agriculture and Engineering, Guangzhou Guangdong
5Institute of Reproductive Medicine, Panyu Hexian Memorial Hospital of Guangzhou, Guangzhou Guangdong
6Guangzhou E-Government Center, Guangzhou Guangdong

Received: Jan. 2nd, 2019; accepted: Jan. 21st, 2019; published: Jan. 28th, 2019

ABSTRACT
In this paper, we establish the random-effect model of bivariate meta-analysis based on the difference mean. Under the assumption of the multilevel normal distribution of the difference mean, we obtain the maximum likelihood estimator
of the difference mean by the method of maximum likelihood estimate. We conclude that the maximum likelihood estimator
of the difference mean is unbiased for the difference mean effect
. In addition, we get the corresponding covariance matrix and the
confidence interval for the difference mean effect
.
Keywords:Meta-Analysis, Maximum Likelihood Estimate, Random-Effect Model

基于均差估计二变量Meta-分析的随机效应 模型
郭鹏飞1,2,3,刘双印2,3,4,李刚5*,张垒2,3,4,曹亮2,3,4,孙向茹6,徐龙琴2,3,4
1仲恺农业工程学院,计算科学学院,广东 广州
2仲恺农业工程学院,广东省高校智慧农业工程研究中心,广东 广州
3仲恺农业工程学院,广东省水禽健康养殖重点实验室,广东 广州
4仲恺农业工程学院,信息科学与技术学院,广东 广州
5广州市电子政务服务中心,广东 广州
6番禺何贤纪念医院,生殖医学科,广东 广州

收稿日期:2019年1月2日;录用日期:2019年1月21日;发布日期:2019年1月28日

摘 要
本文给出已知协方差矩阵的基于均差估值的二变量Meta-分析随机效应模型,并通过极大似然估计法给出效应量估计并说明了其无偏性。通过计算估计效应量的协方差矩阵,给出估计效应分量的
置信区间。
关键词 :Meta-分析,极大似然估计,随机效应模型

Copyright © 2019 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 前言
Meta-分析是一种对同一问题的不同研究进行定量合并的一种方法。该方法是通过考虑每个研究内和研究间的差异性以及研究发表偏倚性得到一个综述结果,从而解决了单个研究样本量小,区域、种族差异大等的缺点。因此Meta-分析的结果对很多领域的科学研究都具有指导意义。针对具体问题的Meta-分析及其统计方法研究已持续了一个世纪之久。最早是在1904年Karl Pearson针对伤寒疫苗效果进行了合并研究 [1] ;接下来的很多年中对某些零星的问题做了类似的综合 [2] 。但是在过去的四十年中,人们逐渐意识到医学实验和临床操作需要基于整体的相关性和可靠证据,Meta-分析的影响得到极大的扩展 [3] 。仅在2018年,关于健康管理的Meta-分析发表文章将近4000篇。
虽然Meta-分析在很多领域都有很好的应用,但对Meta-分析本身的统计方法研究与其应用研究相比就少了很多。从广泛应用的意义上来讲,Meta-分析是以估计量的标准误差为权重的点估计加权平均。随机效应模型的Meta-分析在各个研究效应量不相等这一假设,具体是以估计量方差及研究间差异方差和的逆作为权重得到的加权平均效应量,并可扩展为合并研究间协变量估计 [4] 。
随着数据科学的快速发展,数据维度和数据量急速增加导致单变量Meta-分析无法满足现实应用的需求。多变量Meta-分析有许多优点:第一,可以在一个模型框架下得到所有效应量的估计量;第二,可以通过所有效应量的估计量的协方差矩阵描述多效应量之间的关系。第三,可以获得具有更好统计特性的参数估计量;第四,我们可以获得区别于单变量Meta-分析的潜在机理原因;第五,多变量分析的方法可以在一定程度上降低纳入文献的偏倚性。
由于多变量Meta-分析与单变量Meta-分析比较起来有很多的优点,因此多变量Meta-分析在各个领域的应用研究是很多的。然而,对于多变量Meta-分析本身统计方法的研究却很少。1988年,为了研究教练在SAT中的作用,Raudenbush SW等人通过广义最小二乘法建立了多效应量合并的模型 [5] ;1993年,van Houwelingen HC等人在文献 [6] 首次给出了基于比值比的二变量Meta-分析模型,并讨论了该模型的异质性检验和敏感性分析;1996年,Kalaian HA等人为了研究教练在SAT语言和数学方面的指导效果,在文献 [7] 建立了基于比值比的各研究内效应量不同情形下的多元Meta-分析模型,并通过REML方法估计了效应量的协方差矩阵;2002年,van Houw -elingen HC等人在广义多元混合线性模型的框架下,通过似然估计方法给出了多元Meta-回归模型,并将此模型扩展到了非正态分布情形 [8] 。2008年,Riley RD等人在文献 [9] 中通过极大似然估计法给出了一些特殊相关系数情形下的二变量Meta-分析的协方差矩阵估计;2008年,Ritz J等人在文献 [10] 中通过极大似然估计和估计方程给出了协方差矩阵已知情形下的多元效应量回归参数,并将此模型应用到肺癌发病率的临床推断中。2010年,Paul M等人在文献 [11] 中通过基于可积嵌套拉普拉斯近似的贝叶斯方法给出了多元Meta-分析的合并效应量估计,这种方法得到的方差估计偏移量更小且稳定。
本文通过极大似然估计法给出已知协方差矩阵的基于均差估值的二变量Meta-分析随机效应模型,并通过极大似然估计法给出效应量估计。通过计算估计效应量的协方差矩阵,给出效应分量的
置信区间。
2. 问题描述
在协方差矩阵的基于均差估值的二变量Meta-分析随机效应模型中,我们假设个体量
,
,
和
是独立的并且是正态分布,其均值分别为
,
,
和
,每个研究内的方差分别为
,
。因此
,
,
和
是独立的且服从正态分布,其均值分别为
,
,
和
,方差分别为
,
,
,
。
由上述假设,均差效应量
的分布可表示为:
其中
,
为均值,
,
及
是非随机的。一般地,
,
为未知参数。本文主要内容是通过极大似然估计法来估计
,
。为了方便讨论,记
为研究内均值效应量的协方差矩阵;
为描述研究间关系的协方差矩阵。
3. 均值效应量的极大似然估计
根据之前的假设效应量
服从正态分布,因此关于
的似然函数为:
其中
,
。其所对应的对数似然函数为:
定理3.1:设效应量
服从
的正态分布,则
的极大似然估计量的分量为:
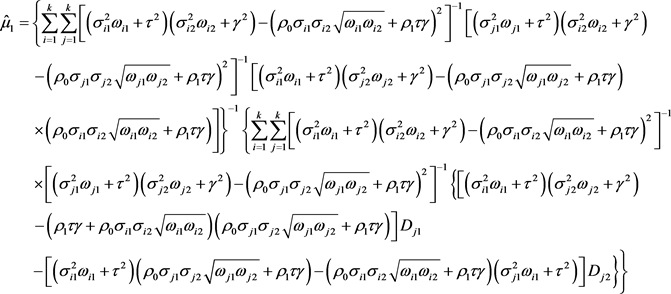
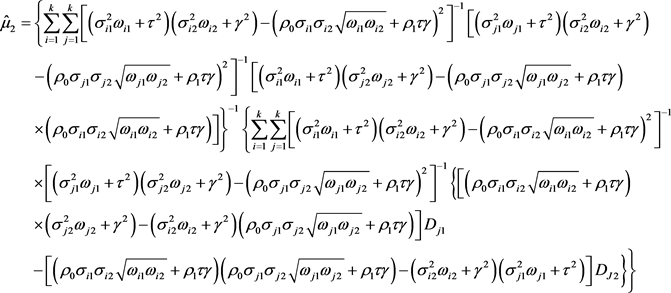
证明:因为关于
的似然函数为:
其所对应的对数似然函数为:
上述对数似然函数对
,
的偏导数为:
令
即得:
整理可得:
因为
可逆,且
为:
其中
,
因此上述关于
,
的线性方程组的解为:
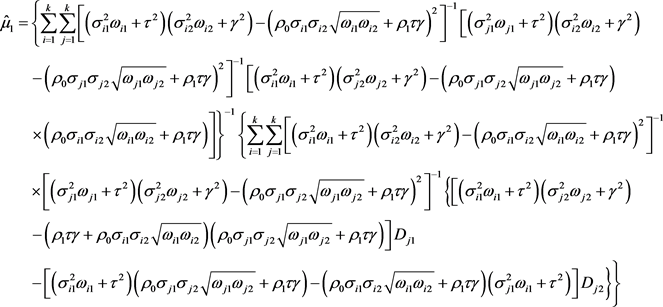
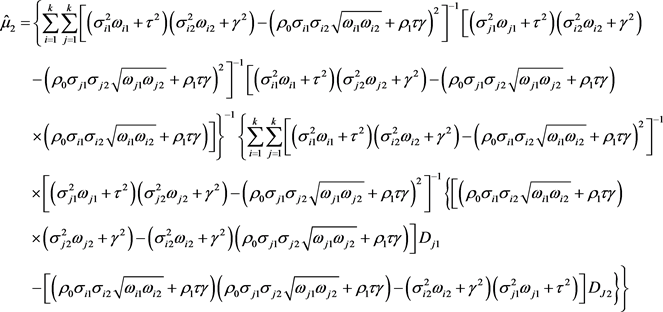
注:由
为:
,
其中
,
可以给出效应量
服从正态分布的合并效应量的矩阵形式为:
。
由上述效应量
服从正态分布的合并效应量均值估计量分量的具体形式,我们可以得到合并效应量均值估计量的如下性质:
性质2.1:设效应量设效应量
服从
的正态分布,其极大似然估计量为:
,则
对于
是无偏的。
证明:要证明估计量的无偏性,需证等式
成立。根据我们给出的效应量
服从正态分布的合并效应量均值估计量分量的具体形式,我们需要证明
,
。因为
,
,所以
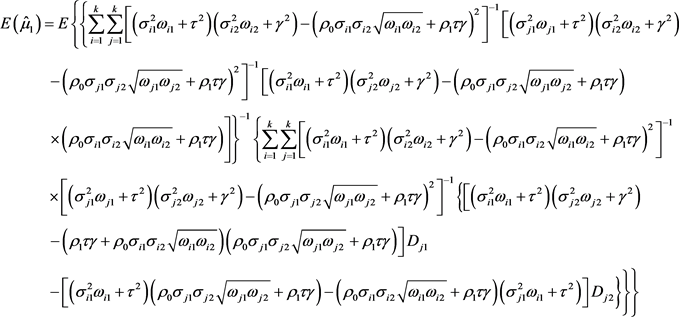

综上所述,
对于
是无偏的。
4. 均值效应量极大似然估计量的协方差矩阵
假设所有的研究都提供所有的均值效应。由多变量统计学的大数定理,合并效应量均值估计量可以近似为一个多元正态分布,其对应的协方差矩阵可由下面的定理给出:
定理4.1:设效应量设效应量
服从
的正态分布,其极大似然估计量为:
,则
所对应的协方差矩阵
为:
,
,
,
。
其中
表示矩阵
第i行第j列的分量,
。
证明:根据多元随机变量的知识可知:如果随机变量
,则
,其中T表示矩阵的转置。由
且
,通过计算可得:
,
。则
因为
,
其中
,可得
所对应的协方差矩阵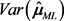 为:
为:
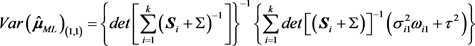 ,
,
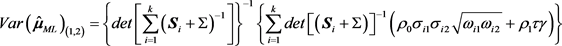 ,
,
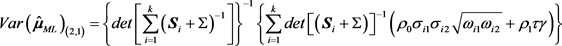 ,
,
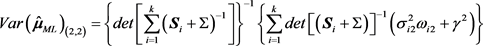 。
。
其中
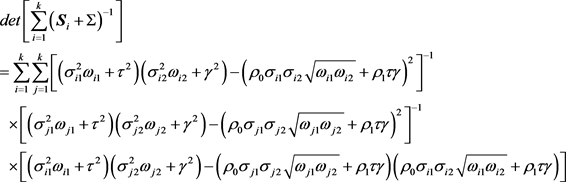
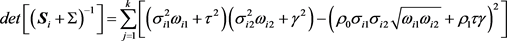 。
。
通过 所对应的协方差矩阵
所对应的协方差矩阵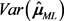 可以给出单变量和联合变量的置信区域,其具体形式为:
可以给出单变量和联合变量的置信区域,其具体形式为:
性质3.1:设效应量设效应量 服从
服从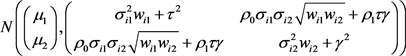 的正态分布,其极大似然估计量为:
的正态分布,其极大似然估计量为: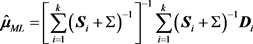 ,则合并均值效应量
,则合并均值效应量 所对应各个分量的
所对应各个分量的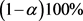 置信区间为:
置信区间为:
 和
和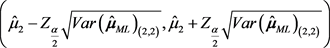 ,其中
,其中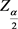 表示正态分布的
表示正态分布的 分位数,
分位数,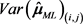 表示矩阵
表示矩阵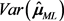 第i行第j列的分量。
第i行第j列的分量。
5. 结束语
本文给出已知协方差矩阵的基于均差估值的二变量Meta-分析随机效应模型,并通过极大似然估计法给出效应量估计。通过计算估计效应量的协方差矩阵,给出效应分量的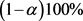 置信区间。这些结论对临床医学,特别是流行病学会有较好的统计学和现实意义。
置信区间。这些结论对临床医学,特别是流行病学会有较好的统计学和现实意义。
基金项目
本项目由如下基金支持:国家自然科学基金(61871475, 61471133, 61571444, 61473331),广东省科技计划(2017B010126001,2017A070712019, 2016A040402043, 2015A070709015, 2015A020209171, 2016B010125004, 2014B040404070,2015A040405014, 2016A070712020),广东省教育厅科技计划(2017GCZX001, 2016KQNCX075, 2016GCZX001, 2017KTSCX094, 2017KTSCX095, 2017KQNCX098),广州市科技计划(201707010221)。
文章引用
郭鹏飞,刘双印,李 刚,张 垒,曹 亮,孙向茹,徐龙琴. 基于均差估计二变量Meta-分析的随机效应模型
The Random-Effect Model of Bivariate Meta-Analysis Based on the Difference Mean[J]. 理论数学, 2019, 09(01): 98-110. https://doi.org/10.12677/PM.2019.91013
参考文献
- 1. Pearson, K. (1904) Report on Certain Enteric Fever Inoculation Statistics. British Medical Journal, 3, 1243-1246.
- 2. Chalmers, I., Hedges, L.V. and Cooper, H. (2002) A Brief History of Research Synthesis. Evaluation and the Health Professions, 25, 12-37.
https://doi.org/10.1177/0163278702025001003
- 3. Lee, W.L., Bausell, R.B. and Berman, B.M. (2001) The Growth of Health-Related Meta-Analyses Published from 1980 to 2000. Evaluation and the Health Professions, 24, 327-335.
https://doi.org/10.1177/01632780122034948
- 4. Normand, S.-L.T. (1998) Tutorial in Biostatistics Meta-Analysis: Formulating, Evaluating, Combining, and Reporting. Statistics in Medicine, 18, 321-359.
- 5. Raudenbush, S.W., Becker, B.J. and Kalaian, H. (1988) Modeling Multivariate Effect Sizes. Psychological Bulletin, 103, 111-120.
https://doi.org/10.1037/0033-2909.103.1.111
- 6. van Houwelingen, H.C., Zwinderman, K.H. and Stijnen, T. (1993) A Bivariate Approach to Meta-Analysis. Statistics in Medicine, 12, 2273-2284.
https://doi.org/10.1002/sim.4780122405
- 7. Kalaian, H.A. and Raudenbush, S.W. (1996) A Multivariate Mixed Linear Model for Meta-Analysis. Psychological Methods, 1, 227-235.
https://doi.org/10.1037/1082-989X.1.3.227
- 8. van Houwelingen, H.C., Arends, L.R. and Stijnen, T. (2002) Advanced Methods in Meta-Analysis: Multivariate Approach and Metaregression. Statistics in Medicine, 21, 589-624.
https://doi.org/10.1002/sim.1040
- 9. Riley, R.D., Abrams, K.R., Lambert, P.C., Sutton, A.J. and Thompson, J.R. (2007) Bivariate Random Effects Meta-Analysis and the Estimation of Between-Study Correlation. BMC Medical Research Methodology, 7, 3.
https://doi.org/10.1186/1471-2288-7-3
- 10. Ritz, J., Demidenko, E. and Spiegelman, D. (2008) Multivariate Meta-Analysis for Data Consortia, Individual Patient Meta-Analysis, and Pooling Projects. Journal of Statistical Plan-ning and Inference, 138, 1919-1933.
https://doi.org/10.1016/j.jspi.2007.07.004
- 11. Paul, M., Riebler, A., Bachmann, L.M., Rue, H. and Held, L. (2010) Bayesian Bivariate Meta-Analysis of Diagnostic Test Studies Using Integrated Nested Laplace Approximations. Statistics in Medicine, 29, 1325-1339.
https://doi.org/10.1002/sim.3858
NOTES
*通讯作者。








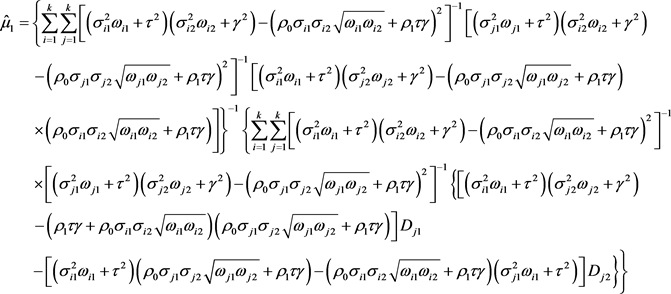
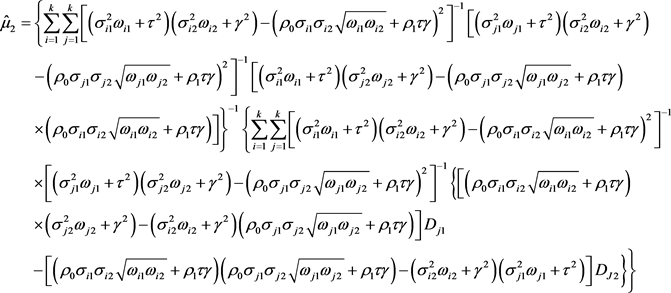
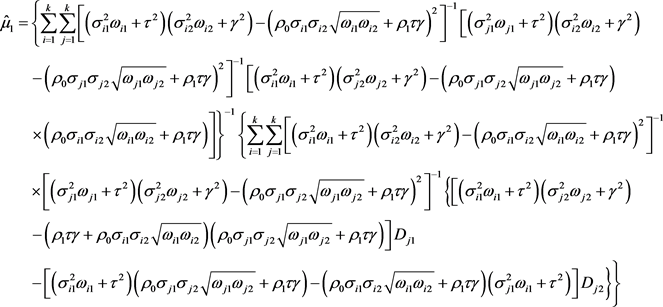
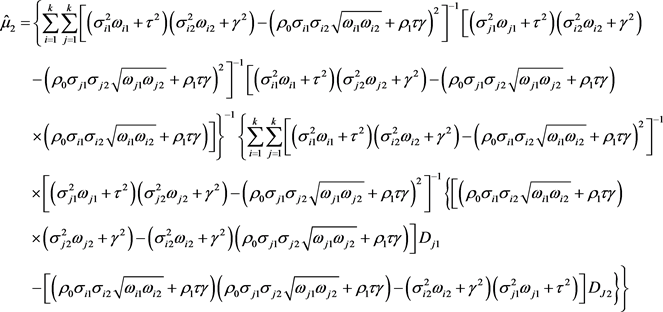
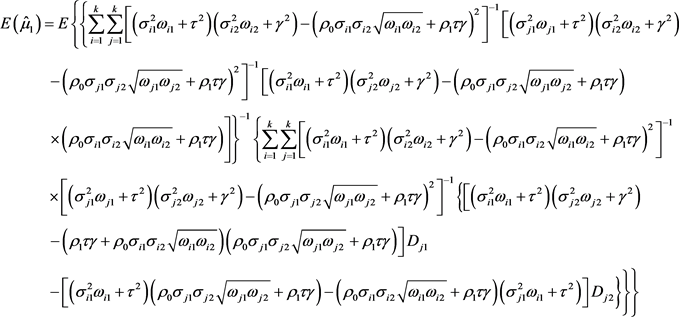

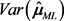 为:
为: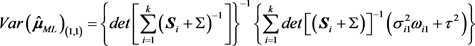 ,
,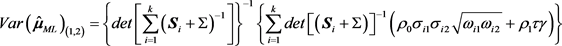 ,
,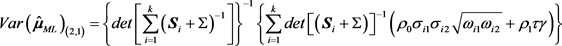 ,
,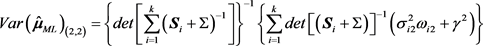 。
。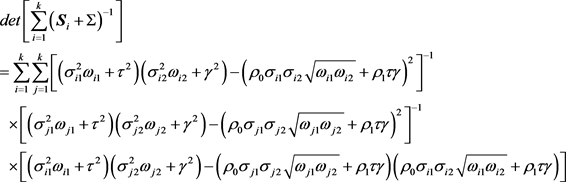
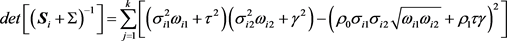 。
。 所对应的协方差矩阵
所对应的协方差矩阵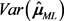 可以给出单变量和联合变量的置信区域,其具体形式为:
可以给出单变量和联合变量的置信区域,其具体形式为: 服从
服从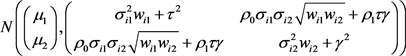 的正态分布,其极大似然估计量为:
的正态分布,其极大似然估计量为: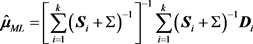 ,则合并均值效应量
,则合并均值效应量 所对应各个分量的
所对应各个分量的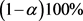 置信区间为:
置信区间为: 和
和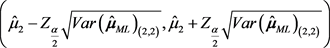 ,其中
,其中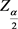 表示正态分布的
表示正态分布的 分位数,
分位数,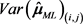 表示矩阵
表示矩阵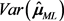 第i行第j列的分量。
第i行第j列的分量。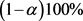 置信区间。这些结论对临床医学,特别是流行病学会有较好的统计学和现实意义。
置信区间。这些结论对临床医学,特别是流行病学会有较好的统计学和现实意义。