Pure Mathematics
Vol.
09
No.
08
(
2019
), Article ID:
32758
,
11
pages
10.12677/PM.2019.98123
Some Infinite Series Involving the Riemann Zeta Function
Wei Ma1, Wanhui Ji2*
1Wuzhong Senior High School, Wuzhong Ningxia
2Ningxia Vocational and Technical College for Nationalities, Wuzhong Ningxia
Received: Oct. 4th, 2019; accepted: Oct. 23rd, 2019; published: Oct. 30th, 2019

ABSTRACT
The series of Riemann functions and the series of hurwitz zeta functions are given by using integral basic identities. The series given is closed. Finally, the numerical series of the zeta function and hurwitz function series are given.
Keywords:Integral Basic Identity, Riemann Zeta Function, Hurwitz Zeta Function
一些涉及黎曼Zeta函数的无穷级数
马玮1,及万会2*
1宁夏吴忠中学,宁夏 吴忠
2宁夏民族职业技术学院,宁夏 吴忠
收稿日期:2019年10月4日;录用日期:2019年10月23日;发布日期:2019年10月30日

摘 要
用积分基本恒等式给出涉及黎曼
函数级数与赫尔维茨zeta函数级数。所给出级数是封闭形的。最后给出关于
函数与赫尔维茨zeta函数级数的数值级数。
关键词 :积分基本恒等式,黎曼zeta函数,赫尔维茨zeta函数

Copyright © 2019 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言与准备
熟知,贝努里数
, 是黎曼zeta函数
;黎曼zeta函数
定义
(1.1)
赫尔维茨函数(黎曼zeta函数
)推广定义
,, (1.2)
黎曼zeta函数的极限值 [1] :
,,, (1.3)
欧拉常数
定义
赫尔维茨函数与黎曼zeta函数关系 [2] [3],
, (1.4)
(1.5)
升阶乘符号:
(1.6)
引理1 [4] 设
为可为函数,则积分基本恒等式成立
引理2 [5] Clausen函数
, ;
,
2. 主要结果与证明
命题1 设
,则黎曼zeta函数
的级数封闭型和式
1)
, (1)
2)
(2)
3)
(3)
4)
(4)
5)
(5)
其中
为Clausen函数
6)
, (6)
7)
, (7)
证明 1) 根据余切函数定义文 [6] ;
, 是贝努里数。
将贝努里数
代入余切表达式,得到关于系数为黎曼zeta 函数
的级数表达式(1)。
2) (1)两端关于x积分,给出(2)式。
3) (2)式两端关于x积分,
积分
,使用分步积分法,利用积分基本恒等式,
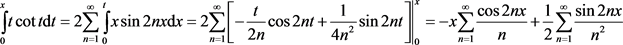 ,
,
由傅里叶级数知,
,所以
(3)式成立。
4) (2)式两端乘以x再关于x积分
使用分步积分法,利用积分基本恒等式
将其代入上式,(4)成立。
5) (2) 式两端乘以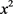 ,再关于x积分
,再关于x积分
我们利用积分基本恒等式计算
将积分
表达式代入上式,得到(5)式。
我们讨论相关交错函数
级数
6) 根据双曲余切函数定义 [6]
,将贝努里数
代入双曲余切表达式得到(6)式。
7) (6)式两端关于x积分得(7)式。命题1证毕。
下面讨论赫尔维茨zeta函数级数封闭形和式。
命题2 设
,则含有升阶乘
的赫尔维茨zeta函数级数封闭形和式
1)
, (8)
2)
(9)
3)
(10)
4)
(11)
5)
(12)
证明 实指数s的二项式展开式为
当
为负实数,即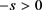 ,利用升阶乘符号
,利用升阶乘符号
同法可得
1)
(1.1)成立。
2) 利用赫尔维茨zeta函数积分公式文 [7],
,对(8)式对
积分1次,2次得到(9),(10)式。
3) 利用赫尔维茨zeta函数微分公式文 [7],
,对(8)式对
微分1次,2次得到(11),(12)式。
命题3设
,则含有升阶乘
赫尔维茨zeta函数级数封闭形和式
1) (13)
(13)
2)
(14)
3)
(15)
4)
(16)
5)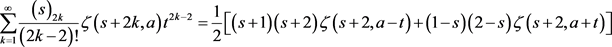 (17)
(17)
证明 1)
(13)式成立。
2) 利用赫尔维茨zeta函数积分公式
,对(13)式对
积分1次,2次得到(14),(15)式。
3) 利用广义黎曼zeta函数微分公式
,对(13)式对
微分1次,2次得到(16),(17)式。
类似命题2的方法可得如下
命题4设
,则含有升阶乘
赫尔维茨zeta函数级数封闭形和式
1)
(18)
2)
(19)
3)
(20)
4)
(21)
5)
(22)
3. 一些与黎曼zeta函数相关的数值级数
(1) 一些关于黎曼zeta函数
的数值级数
在(1)式,令
,有关于
函数的数值级数
1)
;2)
;3)
。
在(2)式,令
,有关于
函数的数值级数
1)
;2)
;3)
。
在(3)式令
,有关于
函数的数值级数
1)
;2)
;
3)
。
这里
是卡大兰常数。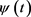 为双伽马函数又称普西函数
是普西函数的导数。这里
为双伽马函数又称普西函数
是普西函数的导数。这里
在(4)式令
,有关于
函数的数值级数
1)
2)
3)
4)
在(5)式,令
,关于
函数的数值级数如下
1)
2)
3)
在(6),(7)式令
,含有黎曼
的交错级数封闭型和式
1)
;
2)
;
3)
;
4)
;
(2) 一些含有升阶乘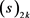 的黎曼zeta函数数值级数
的黎曼zeta函数数值级数
在(13)式,令
,,给出如下含有升阶乘
黎曼zeta函数数值级数
1)
2)
3) 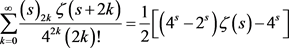
4)
证明 利用赫尔维茨函数与黎曼zeta 函数关系
以及
1) 令
,
2) 令
3) 令
4) 令
文章引用
马 玮,及万会. 一些涉及黎曼Zeta函数的无穷级数
Some Infinite Series Involving the Riemann Zeta Function[J]. 理论数学, 2019, 09(08): 969-979. https://doi.org/10.12677/PM.2019.98123
参考文献
- 1. Abramowitz, M. and Stegun, I.A. (Eds.) (1965) Handbook of Mathematical Functions. Dover Publications, New York, 75, 85.
- 2. Whittaker, E.T. and Watson, G.N. (1963) A Course of Modern Analysis: An Introduction to the General Thoery of Infinite Processes and of Analytic Functions; with an Account of the Principal Transcendental Functions. 4th Edition, Cambridge University Press, Cambridge, London, and New York.
- 3. Titchmarsh, E.C. (1951) The Theory of the Riemann Zeta-Function. Oxford University Press (Clarendon), London.
- 4. Connon, D.F. (2007) Some Series and Integrals Involving the Riemann Zetafunction. Binomial Coefficients and the Harmonic Numbers, 5.
- 5. Berndt, B.C. (1985) Ramanujan’s Notbooks, Part 1. Springger-Verlag, 260-263.
- 6. Boros, G. and Moll, V.H. (2004) Irresistible Integrals: Symbolics, Analysis and Experiments in the Evaluation of Integrals. Cambridge University Press. https://doi.org/10.1017/CBO9780511617041
- 7. Apostol, T.M. (1976) Introduction to Analytic Number Theory. Springer-Verlag, New York, Heidelberg, and Berlin. https://doi.org/10.1007/978-1-4757-5579-4
NOTES
*通讯作者。





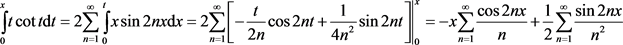 ,
,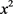 ,再关于x积分
,再关于x积分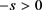 ,利用升阶乘符号
,利用升阶乘符号 (13)
(13)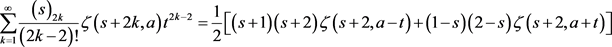 (17)
(17)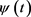 为双伽马函数又称普西函数
是普西函数的导数。这里
为双伽马函数又称普西函数
是普西函数的导数。这里
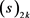 的黎曼zeta函数数值级数
的黎曼zeta函数数值级数