西南交通大学数学学院,四川 成都
收稿日期:2021年12月7日;录用日期:2022年1月13日;发布日期:2022年1月20日

摘要
本文主要考虑在欧式空间中,控制集合是一般可分度量空间的情况下,初始和终端状态满足等式和不等式约束的多目标优化控制问题。讨论其可行解的存在条件,并用不动点定理证明。
关键词
多目标优化控制问题,终端约束,可行解

Existence of the Feasible Solutions for Multiobjective Optimal Control Problems
Jianing Yuan
School of Mathematics, Southwest Jiaotong University, Chengdu Sichuan
Received: Dec. 7th, 2021; accepted: Jan. 13th, 2022; published: Jan. 20th, 2022

ABSTRACT
In this paper, we are devoted to considering the existence of the feasible solutions for multiobjective optimal control problems on Euclidean space, where the endpoints satisfy some equality and inequality type constraints, and the control set is a separable metric space. And we prove it with the fixed point theorem.
Keywords:Multiobjective Optimal Control Problem, Endpoints-Constraint, Feasible Solution

Copyright © 2022 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
令
,,U是度量空间。记
为n维欧式空间,
为从
映到
的绝对连续函数集合,
为从
映到U的可测函数集合。给定映射
,,,,考虑如下控制系统:
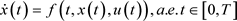 (1)
(1)
其中
, 且满足端点约束
(2)
对于上述系统,记
为所有可行解的集合,即
,其中
为可行控制,
为可行轨线。记
为所有可行控制的集合。
与上述控制系统相关的优化控制问题:
(MCP) 最小化性能指标(目标函数)
(3)
当
时,(MCP)为单目标优化控制问题,当
时为多目标优化控制问题。生活中优化控制的数学模型大都是多目标优化控制问题,例如 [1] 中考虑的三位水平井设计优化问题就是两个目标的优化控制问题; [2] 中废水管理的数学模型所用到的优化控制问题有不止一个目标函数。力学和经济学领域也出现了多目标优化控制问题,为解决此类问题,研究多目标优化控制问题的优化条件是必要的,而在研究这些条件之前,我们必须保证解的存在性。
如今对于多目标优化控制问题的研究大部分对控制集合U是有凸性、闭性或其他要求的,例如 [3] [4] [5] [6] [7] [8] 及其中的参考文献。这就使得结论的适用性非常局限,因为生活中的数学问题大多没有这么好的条件。在本篇论文中,我们只需要U是可分度量空间,来研究这种情况下具有端点约束的多目标优化控制问题可行解的存在性。
此篇论文结构如下:第二部分为主要结论做准备,给出需要的假设、定义和引理;第三部分叙述主要结论;第四部分证明此结论。
2. 准备
首先我们给出定理需要的假设:
(C1) U是一个可分的度量空间;
(C2) 映射
关于t可测,关于x是
的,关于u连续。映射
和
是
的。且存在常数
,存在
,s. t.
对于任意的
,任意的
均成立。
接下来给出一些定义和记号:
Definition 2.1:我们称可行解
为(MCP)的弱有效最优解,如果不存在可行解
,s.t.
。
在这一部分里我们假设
是(MCP)的弱有效最优解。为了方便,对于任意定义在
上的映射
,我们记
。
关于
,我们令
,。
接下来给出证明主要结论需要用到的引理。
Lemma 2.1:令集合
,
其中
对于a.e.
满足
, (4)
则F是凸集。
证明:令
,显然我们只需要证明
是凸集。
对于
,,下证
。
由(4)式,
,。
则
由Liapounoff定理,
,,s.t.
令
,,
,s.t.
.
因此
是凸集,故F是凸集。证毕。
Lemma 2.2:若
,其中
是集合F的内部,则
,,s.t.
,其中
记为集合A的凸包,
是(4)式中
替换为
的解。
证明:事实上,由
, 满足
线性无关,使得
,且
。
Lemma 2.3:对于
,,令
,相应的
满足
, (5)
且
。则
。
证明:由(5)式,
,
由状态方程(1),
。记
其中,
。令
,此时
。
故有
。证毕。
3. 主要结论
这一部分中,我们给出可行控制的存在性定理,也就是本文主要结论。
Theorem 3.1: 假设(C1)-(C2)成立,
是(MCP)的弱有效最优解。若
,则一定能在
附近找到可行控制。即:
,,,满足
,s. t.
。
Remark 3.1: 可行控制的存在性即为可行解的存在性。
4. 证明主要结论
这一部分我们应用第二部分的几个引理和不动点定理证明Theorem 3.1。
Proof: Step 1. 对于
,,s. t.对
, 满足
,使得下述性质成立:
(i)对于任意的
满足
, ;
(6)
, 使得
(7)
其中
满足(6)。
(ii) 令
,即
。记
是以
为控制,以
为初值的轨线,则由Lemma 2.3,
. (8)
与( [6] Lemma 4.5]中的证明相似,我们可以证明
,则(8)式为
. (9)
Step 2. 对于给定的
,存在
,使得
和
满足(6)式,有
.
证明过程与( [6] Lemma 4.5)相似。
Step 3. 由Lemma 2.2及上述证明过程,我们有
定义映射
由Brouwer不动点定理,
满足(6)使得
故有
。
另一方面,当
时,
,
当
时
。
这就说明
。证毕。
文章引用
袁嘉宁. 多目标优化控制问题可行解的存在性
Existence of the Feasible Solutions for Multiobjective Optimal Control Problems[J]. 理论数学, 2022, 12(01): 97-102. https://doi.org/10.12677/PM.2022.121013
参考文献
- 1. Yu, Y.S. and Liu, C.Y. (2007) Optimization of Multi-Objective Optimal Control Problems and Its Application in De-signing of Horizontal Well. Journal of Lanzhou University of Technology, 33, 4.
- 2. Alvarez-Vazquez, L.J., Gar-cia-Chan, N., Martinez, A. and Vazquez-Mendez, M.E. (2010) Multi-Objective Pareto-Optimal Control: An Application to Wastewater Management. Computational Optimization Applications, 46, 135-157.
https://doi.org/10.1007/s10589-008-9190-9
- 3. Kien, B.T., Wong, N.-C. and Yao, J.-C. (2018) Necessary Con-ditions for Multi-Objective Optimal Control Problem with Free End-Time. SIAM Journal on Control and Optimization, 56, 4069-4097. https://doi.org/10.1137/17M1161750
- 4. Kaya, C.Y. and Maurer, H. (2014) A Numerical Method for Nonconvex Multi-Objective Optimal Control Problems. Computational Optimization and Applications, 57, 685-702. https://doi.org/10.1007/s10589-013-9603-2
- 5. Zhu, Q.J. (2000) Hamiltonian Necessary Conditions for a Multiobjective Optimal Control Problem with Endpoint Constraints. SIAM Journal on Control and Optimization, 39, 97-112. https://doi.org/10.1137/S0363012999350821
- 6. Deng, L. and Zhang, X. (2021) Second Order Necessary Conditions for Endpoints-Constrained Optimal Control Problems on Riemannian Manifolds. Journal of Differential Equations, 272, 854-910.
https://doi.org/10.1016/j.jde.2020.10.005
- 7. Bellaassali, S. and Jourani, A. (2004) Necessary Optimality Condi-tions in Multiobjective Dynamic Optimization. SIAM Journal on Control and Optimization, 42, 2043-2061. https://doi.org/10.1137/S0363012902406576
- 8. Ngo, T.-N. and Hayek, N. (2017) Necessary Conditions of Pa-reto Optimality for Multiobjective Optimal Control Problems under Constraints. Optimization, 66, 149-177. https://doi.org/10.1080/02331934.2016.1261349






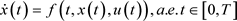 (1)
(1)