Material Sciences
Vol.06 No.06(2016), Article ID:19107,19
pages
10.12677/MS.2016.66053
Models of Diffusion and Stress in Thin Films
Bing Lin, Zhongbao Dai, Mengying Gao, Jiangyong Wang
Department of Physics, Shantou University, Shantou Guangdong

Received: Nov. 4th, 2016; accepted: Nov. 26th, 2016; published: Nov. 30th, 2016
Copyright © 2016 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
Diffusion of atoms in the materials can cause stress, and the produced and/or intrinsic stress may influence the diffusion process, which is more pronounced in the thin films. In this paper, some common diffusion and stress models are summarized and the diffusion equations under stress are deduced based on the thermodynamics. The diffusion profiles with different stress models are then simulated by the finite difference method.
Keywords:Diffusion, Diffusion Coefficient, Diffusion-Induced Stress, Stress-Induced Diffusion

薄膜中的扩散与应力模型
林冰,戴钟保,高梦滢,王江涌
汕头大学物理系,广东 汕头

收稿日期:2016年11月4日;录用日期:2016年11月26日;发布日期:2016年11月30日

摘 要
扩散会产生应力,而产生的或内禀的应力又会影响扩散,这在薄膜材料中表现的尤为突出。本文介绍了常见的几个扩散模型和应力模型,并通过热力学的方法推导出了应力条件下的扩散方程。随后采用有限元差分方法模拟了不同应力模型下的扩散分布。
关键词 :扩散,扩散系数,扩散致应力,应力致扩散

1. 引言
在工业生产和实际应用中,很多物理化学过程都与物质扩散密切相关,如固溶体的形成、相变、固相反应、材料表面处理、半导体掺杂等。在薄膜系统中,薄膜与基底之间由于热膨胀系数不同,或者成分不均匀,会引起应力;应力会引起扩散的改变。这对材料的物理性能有很大的影响,特别是对于一些有害物质的扩散、聚集或者与其他物质发生反应,会对设备的运行安全和使用寿命产生很大的影响,比如,氢致金属脆化 [1] [2] ,渗碳腐蚀 [3] 等现象。
研究扩散现象,还可以解决很多实际问题,比如:寻找Cu与Si之间的最佳的扩散阻挡层 [4] ,防止两者相互扩散形成化合物而导致半导体器件短路;促进半导体扩散工艺的优化 [5] ;以及缓解锂电池电解过程中造成的体积膨胀效应 [6] ,等等。因此,研究应力与扩散的关系,建立合理的扩散模型,至关重要。
研究扩散现象的方法为多学科交叉 [7] 。在连续模型中,涉及连续介质力学和热力学,而相对应的原子模型,则涉及固体物理或者晶体学,这两者可以通过统计力学作为桥梁进行连接。连续模型一般采用有限元差分法进行计算,而原子模型则采用分子动力学或者量子力学。
本文分别对扩散、应力以及扩散应力相耦合的相关理论模型进行了综述。首先介绍了扩散和应力的研究意义和方法,随后介绍了扩散的连续模型和原子模型,接着介绍了几个常见的应力模型。通过热力学理论推导出了应力与扩散相耦合作用下的扩散方程,并对不同应力模型下的扩散进行了模拟。最后对扩散和应力的模型进行总结和展望。
2. 扩散
2.1. 连续模型
1855年,德国生理学家阿道夫·菲克(Adolf Eugen Fick, 1829~1901) [8] 归纳了格雷厄姆(Thomas Graham, 1805~1869)的实验数据 [9] ,并引入扩散系数的概念,将扩散现象用与热学中傅立叶定律(或电学中的欧姆定律)类似的数学式表达,
 (2.1)
(2.1)
 (2.2)
(2.2)
方程(2.1)称为菲克第一定律,方程(2.2)称为菲克第二定律,又称为扩散方程。其中, 是
是 方向上的物质通量,即单位时间
方向上的物质通量,即单位时间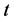 单位面积流过的原子质量;
单位面积流过的原子质量; 是物质浓度;
是物质浓度; 是扩散系数,菲克认为,
是扩散系数,菲克认为,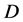 是与自身特性有关的常数。负号表示扩散向着浓度减小的方向。由菲克定律扩散可以看出,只要存在浓度差,扩散就会持续进行,直至达到完全混合,整体平均浓度为
是与自身特性有关的常数。负号表示扩散向着浓度减小的方向。由菲克定律扩散可以看出,只要存在浓度差,扩散就会持续进行,直至达到完全混合,整体平均浓度为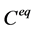 。图1是蔗糖分子在水中的扩散最终达到均匀分布的过程的示意图。
。图1是蔗糖分子在水中的扩散最终达到均匀分布的过程的示意图。
1896年,英国冶金学家威廉·钱德勒·罗伯茨–奥斯汀爵士(Sir William Chandler Roberts-Austen, 1843~1902)将菲克等人的工作从流体扩展至固体的扩散。他通过实验,得出不同温度和时间下,Au在液体Pb和固体Pb中扩散浓度随深度的剖面图 [10] 。随后,斯凡特·阿伦尼斯(Svante Arrhenius, 1859~1927)给出如下扩散系数与温度的关系式 [11]
 (2.3)
(2.3)
上式也称为Arrhenius定律。其中, 是扩散的激活能,
是扩散的激活能, 是玻尔兹曼常数,T是绝对温度,
是玻尔兹曼常数,T是绝对温度, 是指前因子。图2是杂质(Ge, Cu)在单晶Al中的扩散系数 [12] 。由图中可以看出,不同金属杂质在基体中的扩散系数的依赖不同,在500℃的典型值
是指前因子。图2是杂质(Ge, Cu)在单晶Al中的扩散系数 [12] 。由图中可以看出,不同金属杂质在基体中的扩散系数的依赖不同,在500℃的典型值 。一般情况下,将式(2.3)两边取对数,则
。一般情况下,将式(2.3)两边取对数,则

 (a) 糖放在水中 (b) 溶解:分子扩散 (c) 均匀分布
(a) 糖放在水中 (b) 溶解:分子扩散 (c) 均匀分布
Figure 1. Diffusion of sucrose molecules in water
图1. 蔗糖分子在水中扩散示意图
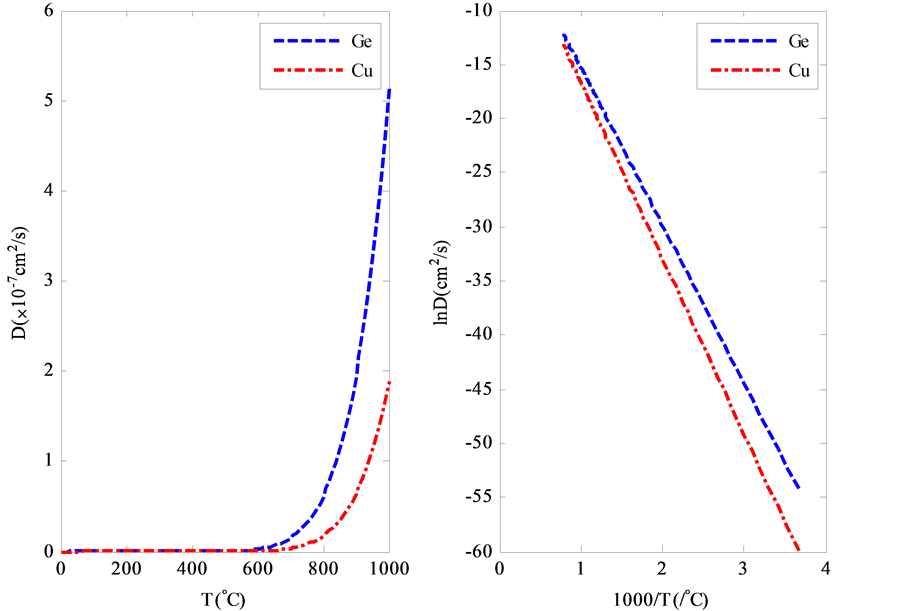
Figure 2. Linear (left) and Logarithmic (right) coordinates of impurity (Ge, Cu) diffusion in Al
图2. 线性坐标(左)和对数坐标(右)下,杂质(Ge, Cu)在单晶Al中的扩散系数与温度的关系
于是, 与
与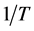 是线性关系(图2右)。其中斜率包含激活能
是线性关系(图2右)。其中斜率包含激活能 的信息。通过获取的
的信息。通过获取的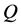 值,可以验证扩散机制。一般情况下,直接替位扩散(
值,可以验证扩散机制。一般情况下,直接替位扩散( )所需激活能最大,间隙扩散次之,而空位扩散所需激活能最小。
)所需激活能最大,间隙扩散次之,而空位扩散所需激活能最小。
至此,方程(2.1)~(2.3)称为扩散连续模型,此后很多结果都建立在这个基础之上 [13] 。扩散模型建立的目的是研究扩散原子在晶体中的分布状况,首先要解出扩散原子浓度 随位置
随位置 和时间
和时间 的变化关系,即
的变化关系,即 。方程(2.2)的解有误差函数解,高斯函数解等 [14] [15] :
。方程(2.2)的解有误差函数解,高斯函数解等 [14] [15] :
 (2.4)
(2.4)
 (2.5)
(2.5)
这两种解法是由于边界条件不同,其中方程(2.4)的误差函数解是,表面焊料的扩散浓度随深度的变化 [16] 。其中, 是初始浓度。
是初始浓度。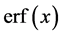 称为误差函数 [17] ,其定义为:
称为误差函数 [17] ,其定义为: ,误差函数的值可以通过误差函数表给出。方程(2.5)的高斯函数解,又称为薄膜解。其中,
,误差函数的值可以通过误差函数表给出。方程(2.5)的高斯函数解,又称为薄膜解。其中, 是
是 处的初始的物质质量。图3给出了误差函数解和高斯函数解的图像 [18] [19] 。
处的初始的物质质量。图3给出了误差函数解和高斯函数解的图像 [18] [19] 。
然而,随着实验现象不断发现,这两个解与实验数据有很大的偏差,这时,人们对开始菲克定律进行修正,认为扩散系数 是一个与浓度
是一个与浓度 有关的变量,称为互扩散系数
有关的变量,称为互扩散系数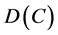 ,则方程(2.2)改写为
,则方程(2.2)改写为
 (2.6)
(2.6)

Figure 3. Gaussian function solution (left) and Error function solution (right) of the diffusion equation
图3. 扩散方程的高斯函数解(左)和误差函数解(右)
显然,方程(2.6)是二阶非线性偏微分方程,对于任意与浓度相关的 ,通常不可能得到它的解析解。做出贡献的是,统计物理学家路德维希·玻尔兹曼(Ludwig Boltzmann, 1844-1906)。他在方程(2.6)中引入新的变量 [20]
,通常不可能得到它的解析解。做出贡献的是,统计物理学家路德维希·玻尔兹曼(Ludwig Boltzmann, 1844-1906)。他在方程(2.6)中引入新的变量 [20]
 (2.6a)
(2.6a)
公式(2.6a)也称为玻尔兹曼变换。采用该变换后,菲克第二定律可以改写为
 (2.6b)
(2.6b)
对扩散偶采用初始条件(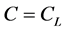 for
for  and
and  for
for ),则每一组元
),则每一组元 的互扩散系数可以由下式给出
的互扩散系数可以由下式给出
 (2.7)
(2.7)
 表示俣野面 [21] (Matano plane)的位置它表示,在某时刻
表示俣野面 [21] (Matano plane)的位置它表示,在某时刻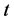 ,流经此面的质量平衡,即流入质量等于流出质量,
,流经此面的质量平衡,即流入质量等于流出质量,
 (2.8)
(2.8)
 表示俣野面上浓度。一般情况下,随着扩散的进行,俣野面会发生迁移,如图4所示。
表示俣野面上浓度。一般情况下,随着扩散的进行,俣野面会发生迁移,如图4所示。
基于式(2.7)和(2.8)的玻尔兹曼–俣野方法,使我们可以在不同温度 中得到
中得到 中提取出扩散系数
中提取出扩散系数 。在通过式(2.3)即可求得,扩散系数–温度的关系
。在通过式(2.3)即可求得,扩散系数–温度的关系 [22] [23] 。
[22] [23] 。

Figure 4. Matano plane drifting during diffusion (dash line is the Matano plane)
图4. 扩散过程中,俣野面迁移示意图(其中虚线表示俣野面的位置)
常见的扩散系数测量方法有:毛细法,转盘法 [24] ,电化学方法 [25] ,光干涉法,放射性同位素法,Taylor分散法,核磁共振法 [26] ,电子显微探针法 [27] 等。
2.2. 原子模型
扩散的本质是原子的随机运动。1827年罗伯特·布朗(Robert Brown)发现悬浮在液体中的花粉颗粒在做无规则的、不间断的运动 [28] ,我们称之为“布朗运动”。1889年法国科学家路易斯·乔治斯·古伊(Louis Georges Gouy, 1854~1926) [29] 研究了不同颗粒在不同液体中的布朗运动。他发现,布朗运动与外力无关,而且在黏滞流体中并不激烈。但是,在1900年以前的科学加并没有能够从定量上描述布朗运动 [30] 。直到1905年爱因斯坦 [31] 和1906年斯莫鲁霍夫斯基 [32] 分别发表了理论上分析布朗运动的文章,这个问题才有所进展。
1905年,阿尔伯特·爱因斯坦(Albert Einstein, 1879~1955)提出扩散系数 、温度
、温度 、溶质粒子半径
、溶质粒子半径 与粘度系数
与粘度系数 之间的关系
之间的关系
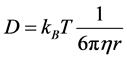 (2.9)
(2.9)
方程式(2.9)称为斯托克斯–爱因斯坦关系, 是斯托克斯力。更一般地,爱因斯坦关系式写为
是斯托克斯力。更一般地,爱因斯坦关系式写为
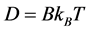 (2.10)
(2.10)
其中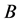 是迁移率,表示单位作用力下的速度。方程式(2.10)也称为爱因斯坦–斯莫鲁霍夫斯关系式。
是迁移率,表示单位作用力下的速度。方程式(2.10)也称为爱因斯坦–斯莫鲁霍夫斯关系式。
1906年,波兰分子统计物理学家玛丽安·斯莫鲁霍夫斯基(Marian von Smoluchowski, 1872~1917)与爱因斯坦建立了布朗运动的统计理论,该理论认为布朗运动实际上代表一种随机涨落现象,涨落可以解释为,原子与布朗颗粒碰撞,并推动其前进 [31] 。该理论在1908年被法国物理学家让·巴蒂斯特·皮兰(Jean Baptiste Perrin)用实验证实 [33] 。
1920年和1921年,奥匈化学家乔治·卡尔·冯·赫维西(Georg Karl von Hevesy, 1885~1966)第一采用同位素标记法分别研究液态Pb [34] 与固态Pb [35] 中的自扩散问题。自扩散与原子跳动频率的关系为
 (2.11)
(2.11)
其中,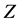 是扩散原子近邻的位置数;
是扩散原子近邻的位置数;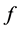 是相关系数,通常
是相关系数,通常 。
。 是相邻格点的间距,即晶格常数。
是相邻格点的间距,即晶格常数。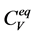 是热平衡时原子的空位浓度,
是热平衡时原子的空位浓度, 是原子进入空位的几率,分别用如下式子表示
是原子进入空位的几率,分别用如下式子表示
 and
and  (2.12)
(2.12)
其中, 是原子跳跃的频率。
是原子跳跃的频率。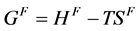 表示空位形成能,包含形成焓
表示空位形成能,包含形成焓 和形成熵
和形成熵 ;
; 是空位迁移能,同理,也包含熵和焓。将式(2.12)代入式(2.11)中,并化简
是空位迁移能,同理,也包含熵和焓。将式(2.12)代入式(2.11)中,并化简
 (2.13)
(2.13)
式(2.13)与式(2.5)一致,其中,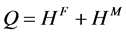 称为扩散激活能。
称为扩散激活能。
实验上的另一个突破来自美国冶金学家欧内斯特·柯肯达尔 [36] (Ernest Kirkendall, 1914~2005)。在20世纪40年代,人们普遍认为金属中的原子扩散是通过换位机制或者环形机制。这就意味着,二元合金中各成分的扩散速率相同。但是,柯肯达尔发现,在黄铜(Cu + 30wt.%Zn)与纯铜组成的扩散对中,Zn向外扩散的速度比Cu向内扩散的速度快,最好的证明,就是钼丝移动。该现象导致了空位机制的出现,在1948年由Darken [37] 给出理论分析。
1951年,人们发现,原子沿晶界扩散的速度比在晶格中的扩散速度快,系数之比甚至达到5个数量级 [38] 。同年,费舍 [39] 和特恩布尔 [40] 分别开始了对晶界扩散的定量研究。这在多晶特别是纳米晶体,薄膜或者多层膜器件中起重要作用。
2.3. 热力学分析
菲克第一定律认为扩散的结果导致浓度梯度的减小,成分分布趋于均匀。然而,并非所有的扩散过程都是如此,物质可以从低浓度区向高浓度区扩散,扩散的结果提高了浓度。例如,Sn在Cu单晶中的偏析 [41] [42] [43] ,以及某些合金固溶体调幅分解形成的溶质原子富集区 [44] 等,这种扩散称为“上坡扩散”或“逆向扩散”。从热力学分析可知,扩散的驱动力是化学势梯度 ,由此不仅能解释通常的扩散现象,也能解释“上坡扩散”等反常扩散现象 [45] 。
,由此不仅能解释通常的扩散现象,也能解释“上坡扩散”等反常扩散现象 [45] 。
在热力学中,化学势 表示每个
表示每个 原子的亥姆霍兹自由能,也称为偏摩尔自由能,即
原子的亥姆霍兹自由能,也称为偏摩尔自由能,即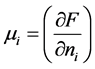 ,
,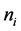 是组元
是组元 的原子数。原子所受的驱动力
的原子数。原子所受的驱动力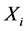 可从化学势对距离求导得到:
可从化学势对距离求导得到:
 (2.14)
(2.14)
式中,负号表示驱动力与化学势下降的方向一致,也就是扩散总是向化学势(能量)减小的方向进行,即在等温等压条件下,只要两个区域中 组元存在化学势差
组元存在化学势差 ,就能产生扩散,直至
,就能产生扩散,直至 。
。
在化学势的驱动下,扩散原子在固体中沿给定的方向运动时,会受到固体中溶剂原子的阻力,阻力与扩散速度成正比。当溶质原子扩散加速到其受到的阻力等于驱动力时,溶质原子的扩散速度就达到了它的极限速度,也就达到了原子的平均扩散速度,即扩散原子的速度等于溶质原子的速度。原子的平均扩散速度 正比于驱动力X:
正比于驱动力X:
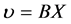 (2.15)
(2.15)
比例系数 为迁移率,见公式(2.10)。扩散通量可以等于扩散原子的质量浓度与其平均速度的乘积:
为迁移率,见公式(2.10)。扩散通量可以等于扩散原子的质量浓度与其平均速度的乘积:
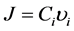
由此可得

利用爱因斯坦关系(2.10),即可得
 (2.16)
(2.16)
定义浓度分数

在理想溶液模型中,化学势可以写为:
 (2.17)
(2.17)
其中, 称为标准化学势,即
称为标准化学势,即 。
。 表示由于温度升高,粒子重新排布引起的熵的增加,从而化学势的变化。将(2.17)代入(2.16)得菲克第一定律,即公式(2.2)。
表示由于温度升高,粒子重新排布引起的熵的增加,从而化学势的变化。将(2.17)代入(2.16)得菲克第一定律,即公式(2.2)。
3. 应力
几乎所有的金属和无机非金属薄膜都处于应力状态。应力来源于两部分,分别是热应力和内应力。热应力是由于衬底与薄膜之间的热膨胀系数不同而引起的。内应力是薄膜在沉积过程中,扩散时质量前移导致晶格畸变以及缺陷不断累积的效果 [46] 。这个过程会引起横向应力的变化,也称为扩散致应力。扩散致应力最早发现于固态半导体装置的研究中 [47] 。当结构中物质扩散产生的应力足够大时,会产生位错,影响掺杂原子的分布,进而对半导体结构的性能产生一定的影响。因此,很多研究者通过模拟来分析结构中质量迁移产生的应力及其分布。
Prussin [48] 最早提出了扩散致应力的概念。他认为,固体中浓度梯度引起的应力,与无受力固体中温度梯度引起的应力类似,都有一个线性应变系数,即
 (3.1)
(3.1)
其中,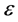 是应变,
是应变, 是膨胀系数,
是膨胀系数, 表示此时的浓度。同时,他还给出了厚度为
表示此时的浓度。同时,他还给出了厚度为 的薄板中扩散致应力的表达式
的薄板中扩散致应力的表达式
 (3.2)
(3.2)
Li [49] 对一些简单形状(薄板,圆柱,球形)进行试验,并给出了(3.1)式中的膨胀系数值, ,其中,
,其中,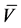 为摩尔体积。
为摩尔体积。
Larch和Cahn [50] [51] [52] 建立了固体结构中局部扩散通量和由于多相存在或者不均匀分布产生的应力之间的关系,以此为基础的理论预测模型可用于定性,在某些情况下可以定量描述上坡扩散问题。他们给出的厚度为L的薄板应力表达式 [53]
 (3.3)
(3.3)
其中, 表示扩散组元
表示扩散组元 在薄膜内的平均成分,
在薄膜内的平均成分, 表示薄膜厚度,
表示薄膜厚度, 表示薄膜的杨氏模量。
表示薄膜的杨氏模量。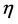 是一个系数,与式(3.2)中的
是一个系数,与式(3.2)中的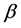 一致。由此,式(3.2)与式(3.3)一致。括号中的第三项表示薄板自由端的弯曲情况,如果考虑镀在衬底上的薄膜,则可以将其忽略。
一致。由此,式(3.2)与式(3.3)一致。括号中的第三项表示薄板自由端的弯曲情况,如果考虑镀在衬底上的薄膜,则可以将其忽略。
考虑浓度分布为误差函数分布情况下应力的演变情况,如图5所示。可以看出,扩散导致的正应力是压应力,应力大小与浓度差成正比;同时,应力沿扩散方向经历从压应力到拉应力的过度,且在浓度差较大的区域处于受压状态,而在浓度差比较小或者无浓度差的区域受拉。同时,随着时间的推移,扩散浓度趋于均匀,扩散应力可以近似为线性应力。可以推测,当 时,扩散应力将趋于零,金属内部达到完全的无应力膨胀状态 [54] 。
时,扩散应力将趋于零,金属内部达到完全的无应力膨胀状态 [54] 。
1999年,Gao等人 [55] [56] 研究直接镀在衬底上的金属多晶薄膜的晶界扩散,发现扩散过程中会形成与裂纹类似的楔形晶界。在他们的模型中,假设晶界平行于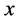 轴方向,由于质量迁移产生的应力效果类似于在与
轴方向,由于质量迁移产生的应力效果类似于在与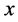 轴垂直的方向上,某个
轴垂直的方向上,某个 处插入沿
处插入沿 轴方向的位错 [57] 。楔形的插入,晶格收到挤压,引起垂直晶界方向的应力变化,邻近原子沿晶界扩散,其作用相当于产生一个沿晶界方向的正向牵引,如图6所示。
轴方向的位错 [57] 。楔形的插入,晶格收到挤压,引起垂直晶界方向的应力变化,邻近原子沿晶界扩散,其作用相当于产生一个沿晶界方向的正向牵引,如图6所示。
由此,薄膜中的应力可以表示为
 (3.4)
(3.4)

Figure 5. Error function diffusion profiles (left) and corresponding stresses (right) at different times
图5. 不同时间点误差函数浓度分布(左)以及与之对应的扩散应力分布(右)
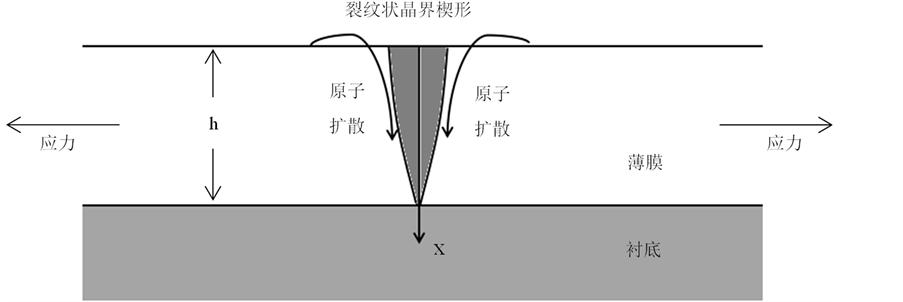
Figure 6. The geometry of a crack-like grain-boundary wedge
图6. 裂纹状晶界楔形示意图
其中, 是与位错有关的柏氏矢量,
是与位错有关的柏氏矢量,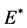 是有效弹性模量,其表达式为
是有效弹性模量,其表达式为

这里, 是各向同性杨氏模量,
是各向同性杨氏模量, 是泊松比。
是泊松比。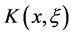 是Kernel函数,当系统中只有一个楔形的时候,比如双晶体系 [58]
是Kernel函数,当系统中只有一个楔形的时候,比如双晶体系 [58]
 (3.5)
(3.5)
对(3.4)进行积分,即得到仅沿 轴方向的应力,表达式为
轴方向的应力,表达式为
 (3.6)
(3.6)
其中,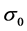 是初始应力,
是初始应力, 是位错密度,
是位错密度,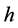 是金属膜的厚度。假设
是金属膜的厚度。假设 ,图7分别给出了位错密度随宽度变小(
,图7分别给出了位错密度随宽度变小( ),变大(
),变大( )以及不变(
)以及不变( )情况下,晶界应力随深度的变化。
)情况下,晶界应力随深度的变化。
无论 随宽度如何变化,扩散引起的正应力为压应力,并且,沿着扩散方向经历从受压到拉伸状态。
随宽度如何变化,扩散引起的正应力为压应力,并且,沿着扩散方向经历从受压到拉伸状态。
2003年,陈永翀等人基于流体力学的基本概念和方法,推导建立了描述固体互扩散生长的普适方程 [59] ,讨论了应力与扩散的相互关系 [60] ,区别了体积生长和界面生长 [61] ,并给出了固态反应周期层片的理论描述 [62] [63] 。普适方程为:
 (3.7)
(3.7)
式中, 是组元
是组元 的密度,
的密度, 是组元
是组元 的扩散通量,
的扩散通量,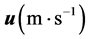 是原子的速度,
是原子的速度, 是原子
是原子 的有效体积,
的有效体积, 是原子质量。原子的速度
是原子质量。原子的速度 可由互扩散区域的内的惰性标记近似测定,散度
可由互扩散区域的内的惰性标记近似测定,散度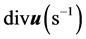 等价于体积生长率。他给出的扩散应力为
等价于体积生长率。他给出的扩散应力为
 (3.8)
(3.8)
式中 是扩散系数,
是扩散系数,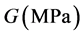 是剪切模量,
是剪切模量,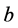 是位错的柏格斯矢量,
是位错的柏格斯矢量, 是晶格常数,
是晶格常数, 是一个无量纲常数,
是一个无量纲常数, 和
和 为待定指数。
为待定指数。
2005年,Jay Chabraborty [64] 基于Larhe-Cahn理论,针对置换固溶体严格推导建立了非静水应力扩散模型,并以Pd-Cu和Au-Ni二元扩散偶为例数值模拟了非静水压和自应力下所发生的特殊扩散现象。Chabraborty采用误差函数型应力,应力梯度仅局限在薄膜的界面区域,其描述为
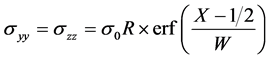 (3.9)
(3.9)
其中, 表示应力参考量(取600 MPa),
表示应力参考量(取600 MPa), 表示应力相对参考应力的相对大小,
表示应力相对参考应力的相对大小, 表示无量纲化位置,
表示无量纲化位置,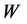 表示界面处的控制参量,
表示界面处的控制参量,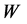 越小,界面处应力梯度越大。图8中给出了当应力为误差型时,其值随深度的变化。其中,左图为
越小,界面处应力梯度越大。图8中给出了当应力为误差型时,其值随深度的变化。其中,左图为 不变(= 0.05),
不变(= 0.05), 变化(= −10,−5,0,5,10)时,应力的演化情况;右图为
变化(= −10,−5,0,5,10)时,应力的演化情况;右图为 不变(= 5),
不变(= 5), 变化(= 0.01,0.03,0.05,0.1,0.2)时,应力随深度的变化情况。
变化(= 0.01,0.03,0.05,0.1,0.2)时,应力随深度的变化情况。
2010年,Moskalioviene等人 [65] [66] [67] 根据Onsager理论 [68] 模拟计算了N在渗氮铁中发生应力致间隙扩散导致的深度剖面,很好的与实验数据相吻合。他们采用的应力为 [69]
 (3.10)
(3.10)
其中, 是杨氏模量,
是杨氏模量,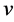 是泊松比,
是泊松比, 是平衡浓度,
是平衡浓度,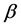 是Vegard常数。在奥氏体中,
是Vegard常数。在奥氏体中, ,
, ,,
,, ,则应力为
,则应力为 。浓度引起的应力为压应力,大约是GPa量级 [70] [71] 。由于固体中应力的缓解,可以简化成线性应力
。浓度引起的应力为压应力,大约是GPa量级 [70] [71] 。由于固体中应力的缓解,可以简化成线性应力
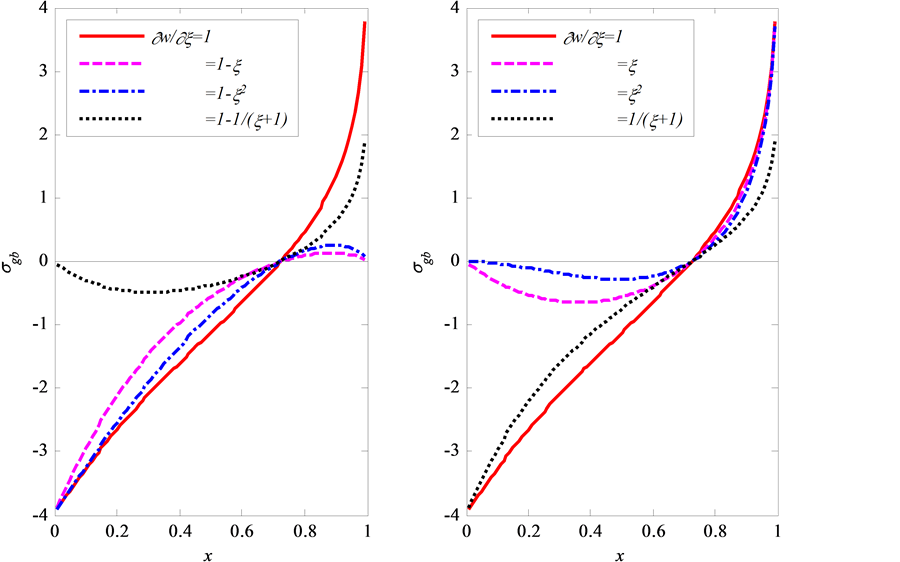
Figure 7. The variation of the grain boundary stresses with depth as the dislocation density decreases (left) and increases (right)
图7. 位错密度随宽度减小(左)和增大(右)情况下,晶界应力随深度的变化
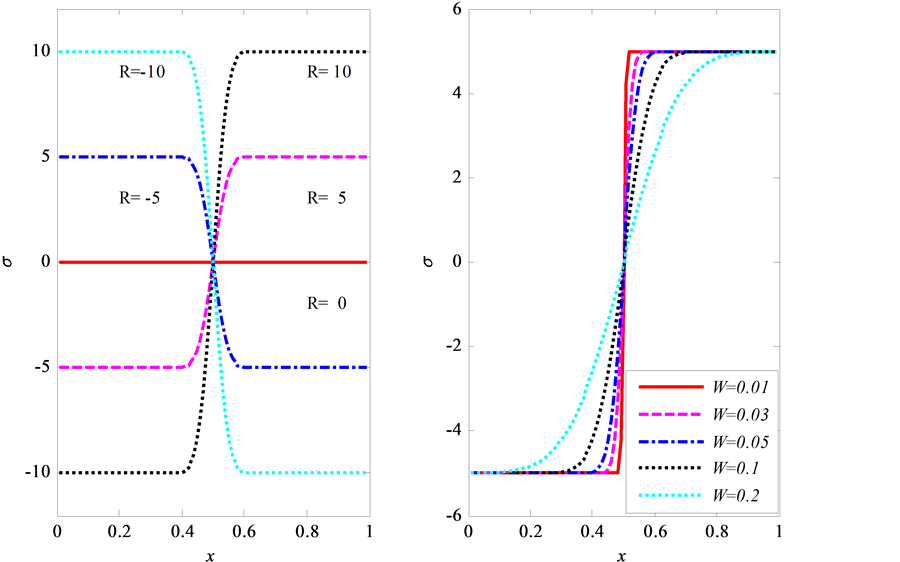
Figure 8. Different error type stresses (Left: W = 0.05, R = −10, −5, 0, 5, 10; Right: R = 5, W = 0.01, 0.03, 0.05, 0.1, 0.2)
图8. 误差型应力随深度的变化(左图W = 0.05,R = −10,−5,0,5,10;右图R = 5,W = 0.01,0.03,0.05,0.1,0.2)
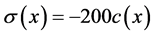 (3.11)
(3.11)
迄今,还没有一个统一有效的扩散致应力模型。
4. 应力对扩散的影响
固体内质点的受力情况,可以用一个应力张量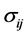 表示。而应力张量又可以分为,静水应力和非静水应力(图9)。
表示。而应力张量又可以分为,静水应力和非静水应力(图9)。 可以写为
可以写为

假设物体仅受正应力,则应力张量中除了对角线上的值,其他值都为零,即
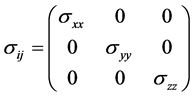
静水应力是应力球张量,即各个面所受的应力相同,其作用效果是质点体积改变,常用于流体和部分可压缩固体。静水应力条件下,应力张量可以写为
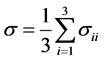 (4.1)
(4.1)
非静水应力是应力偏张量,每个面受力不同,其作用效果将使质点发生形状畸变。基本上认为所有受力固体均为非静水应力系统。非静水应力条件下,应力张量 至今还没有统一的表达式【见第3部分】。
至今还没有统一的表达式【见第3部分】。
下面给出应力条件下的化学势的推导过程:
应力条件下,亥姆霍兹自由能(Helmholtz free energy) 的微分形式表示为
的微分形式表示为
 (4.2)
(4.2)
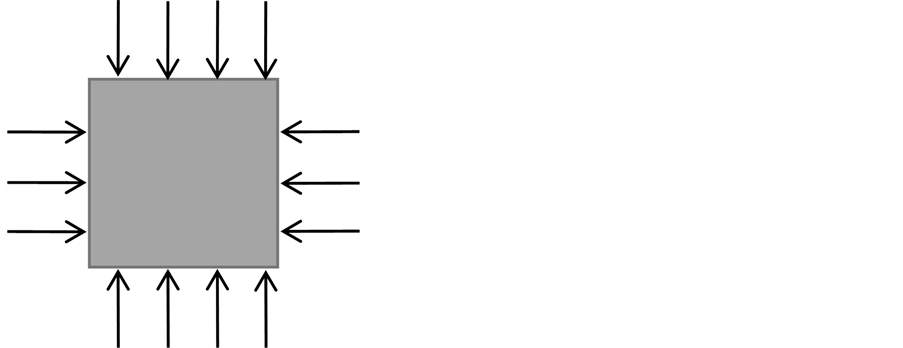
Figure 9. Sketch of solid under hydrostatic pressure (left) and non-hydrostatic pressure (right). The arrow indicates the direction of pressures and the density of arrow represents the pressure value
图9. 固体受静水应力(左)与非静水应力(右)示意图。其中,箭头方向表示受力方向,箭头密度表示力的相对大小
其中,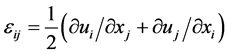 是应变张量,
是应变张量,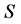 是熵,
是熵,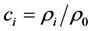 是组元i的摩尔浓度分数,其中
是组元i的摩尔浓度分数,其中 (摩尔数/体积)是摩尔浓度,
(摩尔数/体积)是摩尔浓度, 。
。 是单位摩尔混合物体积,
是单位摩尔混合物体积,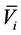 是组元i的摩尔体积。
是组元i的摩尔体积。
在化学平衡条件下,系统的能量最小 。同时必须满足熵值守恒
。同时必须满足熵值守恒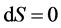 (4.2-1),原子守恒
(4.2-1),原子守恒 (4.2-2)。采用拉格朗日乘数法求解约束条件(4.2-1)和(4.2-2)下的系统平衡问题,解出
(4.2-2)。采用拉格朗日乘数法求解约束条件(4.2-1)和(4.2-2)下的系统平衡问题,解出
 (平衡态下,均为常数) (4.3)
(平衡态下,均为常数) (4.3)
其中,M是原子的扩散势,假设系统中有A、B两种原子,则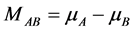 ,若只有A原子(或者更特殊情况下,A也是空位),即B原子为空位时,
,若只有A原子(或者更特殊情况下,A也是空位),即B原子为空位时,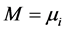 。
。
将(4.3)代入式(4.2)中,有
 (4.4)
(4.4)
将 写成全微分形式,并联立(4.4)式,对变量
写成全微分形式,并联立(4.4)式,对变量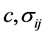 满足麦克斯韦关系
满足麦克斯韦关系
 (4.5)
(4.5)
系统的总应变 可以写成 [72]
可以写成 [72]
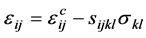 (4.6)
(4.6)
这里, 是应力为零时,浓度从
是应力为零时,浓度从 变化到
变化到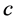 产生的应变;第二项表示浓度为
产生的应变;第二项表示浓度为 ,在应力
,在应力 作用下的应变。
作用下的应变。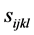 是弹性柔性系数,为四阶张量。假设系数
是弹性柔性系数,为四阶张量。假设系数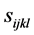 与浓度的关系可以忽略,并定义化学膨胀系数张量
与浓度的关系可以忽略,并定义化学膨胀系数张量 [73] ,则
[73] ,则
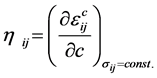 (4.7)
(4.7)
立方材料中,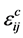 各向同性,此时
各向同性,此时 。对于二元立方材料,
。对于二元立方材料, 与组元的偏摩尔体积
与组元的偏摩尔体积 相关,
相关,

将式(4.6)和(4.7)代入(4.5),并进行积分。在各向同性情况下,求解应力 对扩散势
对扩散势 的影响
的影响
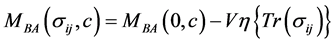 (4.8)
(4.8)
其中 是无应力条件下的扩散势,即
是无应力条件下的扩散势,即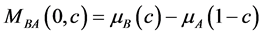 ;假设系统受到静水应力,即
;假设系统受到静水应力,即
 (4.9)
(4.9)
则(4.8)式可以改写为
 (4.10)
(4.10)
式(4.10)即为应力作用下的平衡态方程。假设方程左右两边等于一个常数,并假设这个常数为零。则有
 (4.11)
(4.11)
采用固溶体模型,即 ,代入方程(4.11),则组元i处于浓度为
,代入方程(4.11),则组元i处于浓度为 ,应力为
,应力为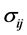 条件下的化学势为
条件下的化学势为
 (4.12)
(4.12)
上式代入式(2.16),得到包含浓度和扩散应力的扩散通量表达式
 (4.13)
(4.13)
定义广义扩散系数:

将式(4.13)写成菲克第一定律的形式,即

由菲克第二定律可得到瞬态的扩散方程
 (4.14)
(4.14)
更一般地,驱动力是扩散势的梯度,则
 (4.15)
(4.15)
同理,瞬态扩散方程为
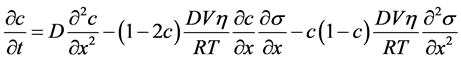 (4.16)
(4.16)
如果考虑应力影响扩散的同时,造成原子的积累或者空位的积累,此时形成Gao模型中的楔形部分,应力得到缓解 [74] 。假设楔形宽度为w,薄膜扩散区宽度为δ,则瞬态扩散方程为
 (4.17)
(4.17)

该模型是否能成功应用于扩散现象的研究,仍有待实验证实。
5. 应力作用下扩散的模拟
5.1. Cahn应力模型下的模拟
由【第4部分】推导出的扩散通量表达式为,
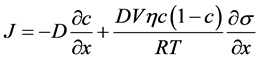 (5.1)
(5.1)
Larche和Cahn的应力模型为,
 (5.2)
(5.2)
先对应力求导,则
 (5.3)
(5.3)
将上式代入公式(5.1),则
 (5.4)
(5.4)
于是,瞬态扩散方程为
 (5.5)
(5.5)
引入无量纲参量
 (5.6)
(5.6)
考虑镀在刚性衬底上的薄膜,则忽略(4.5)式中的第三项,于是(4.5)式可以改写为
 (5.7)
(5.7)
边界条件为
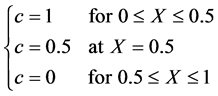 (5.8)
(5.8)
采用有限差分方法进行计算,结果如图10所示。从图中可以看出,随着时间的推移,应力更趋平缓并趋向于零。同时,在应力作用下,浓度剖面更加平缓,即应力作用下,更快达到平衡。
5.2. Gao应力模型下的模拟
同理,对于式(4.16)和(4.17),引入无量纲参量
 (5.9)
(5.9)
则无量纲扩散方程为
 (5.10)
(5.10)

Figure 10. The evolution of stress at different times (number of time steps: 100, 1000, 5000, 10,000) (left) and the concentration under stress and stress free (right, number of time steps: 10,000)
图10. 不同时刻(时间步数分别为100,1000,5000,10,000)的应力演化情况(左),以及应力对浓度的影响(对应时间步数为10,000)
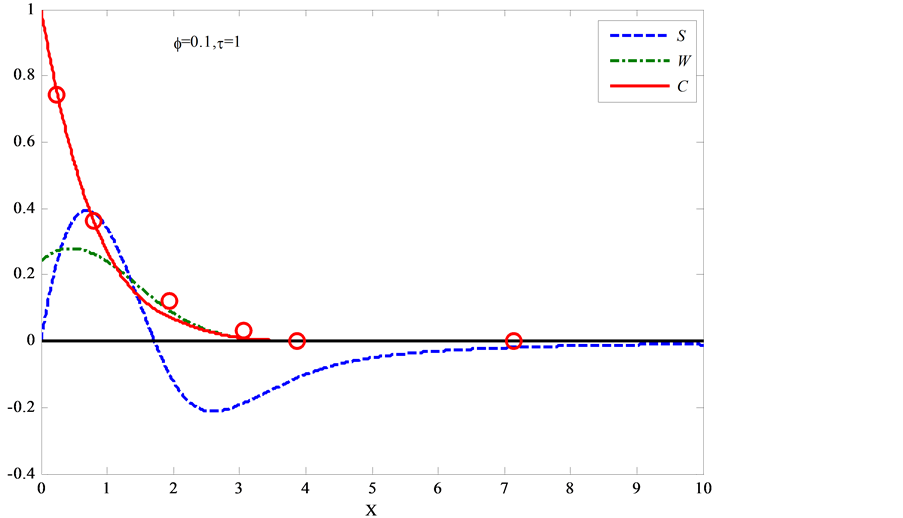
Figure 11. The calculation dependencies of the dimensionless GB concentration (CB), the normal GB stress (S), and the width of the wedge (W) on the penetration depth along the GB for φ = 0.1 and τ = 1
图11. 根据文献 [74] 求解方程(5.10)得出浓度CB,应力S(注意:此模型中压应力为正值),楔形宽度W随深度的演化图,图中红色圈为文献 [74] 中数值模拟CB值
其中,参数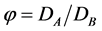 。
。
同样采用有限差分的方法解上述方程,可以得到应力S,楔形宽度W,浓度C随深度的演化,如图11。从图中可以看出,在晶界(GB)扩散区域,同时有压应力和拉伸应力产生。在双晶体表面区域(即扩散源)附近,产生压应力,而距离扩散源较远的地方为拉伸应力。
6. 总结与展望
文章介绍了扩散模型和应力模型的历史发展,并推导了应力作用下的扩散方程。目前,对扩散应力的研究,主要是将应力简化为静水应力,然后利用玻尔兹曼–俣野的方法,提取出扩散系数,从而对扩散现象进行描述。而在非静水应力的研究中,由于没有统一的扩散应力模型,而且实验上很难进行测量,比如,固相形成将会掩盖应力的影响,所以,至今没有较为完善的理论模型,而这可以从以下两个方面进行尝试:第一,通过实验测量,修正已有的应力模型;第二,将已有的应力模型应用于扩散方程,结合实验数据,不断进行完善和修正。
基金项目
本工作受到国家自然基金(No. 11274218)和中国–以色列国际间合作与交流项目(NSFC-ISF)资助。
文章引用
林 冰,戴钟保,高梦滢,王江涌. 薄膜中的扩散与应力模型
Models of Diffusion and Stress in Thin Films[J]. 材料科学, 2016, 06(06): 413-431. http://dx.doi.org/10.12677/MS.2016.66053
参考文献 (References)
- 1. Louthan, M.R., Caskey, G.R., Donovan, J.A.,, Rawl Jr., D.E. (1972) Hydrogen Embrittlement of Metals. Materials Science and Engineering, 10, 357-368. https://doi.org/10.1016/0025-5416(72)90109-7
- 2. Shih, D.S., Robertson, I.M. and Birnbaum, H.K. (1988) Hydrogen Embrittlement of α Titanium: In Situ TEM Studies. Acta Metallurgica, 36, 111-124. https://doi.org/10.1016/0001-6160(88)90032-6
- 3. 张俊善. 材料的高温变形与断裂[M]. 北京: 科学出版社, 2007: 489-493.
- 4. 张在玉, 陈秀华. Cu在CoN和CoSiN薄膜中的扩散研究[J]. 怀化学院学报, 2013, 32(5): 27-32.
- 5. 王玉中, 赵寿南. 硅扩散应力的理论分析[J]. 华南理工大学学报: 自然科学版, 1995, 23(12): 38-45.
- 6. Baker, D.R., Verbrugge, M.W. and Bower, A. (2016) Thermodynamics, Stress, and Stefan-Maxwell Dif-fusion in Solids: Application to Small-Strain Materials Used in Commercial Lithium-Ion Batteries. Journal of Solid State Electrochemistry, 20, 163-181. https://doi.org/10.1007/s10008-015-3012-7
- 7. Diaz, A., Alegre, J. and Cuesta, I.I. (2016) A Review on Diffusion Modelling in Hydrogen Related Failures of Metals. Engineering Failure Analysis, 66, 577-595. https://doi.org/10.1016/j.engfailanal.2016.05.019
- 8. Fick, A. (1855) Ueber Diffusion. Annalen der Physik, 170, 59-86. https://doi.org/10.1002/andp.18551700105
- 9. Graham, T. (1950) The Bakerian Lecture: On the Diffusion of Liquids. Philosophical Transactions of the Royal Society of London Series A, 140, 1-46. https://doi.org/10.1098/rstl.1850.0001
- 10. Roberts-Austen, W.C. (1896) Bakerian Lecture: On the Diffusion in Metals. Philosophical Transactions of the Royal Society of London Series A, 187, 383-415. https://doi.org/10.1098/rsta.1896.0010
- 11. Arrhenius, S. (1889) Über die Reaktionsgeschwindigkeitbei der Inversion von Rohrzuckerdurch Säuren. Zeitschrift für Physikalische Chemie, 4, 226-248.
- 12. Peterson, N.L. and Rothman, S.J. (1970) Impurity Diffusion in Aluminum. Physical Review B, 1, 3264-3273. https://doi.org/10.1103/PhysRevB.1.3264
- 13. Salamon, M. and Mehrer, H. (2005) Interdiffusion, Kirkendall Effect, and Al Self-Diffusion in Iron-Aluminiumalloys. Zeitschrift fur Metallkunde, 96, 4-16. https://doi.org/10.3139/146.018071
- 14. Shewmon, P. (1989) Diffusion in Solids. The Minerals, Metals & Materials Society, Diffusion in Solids. 2nd Edition, Retroactive Coverage, United States, 246.
- 15. Crank, J. (1975) The Math-ematics of Diffusion. 2nd Edition, Clarendon Press, Clarendon.
- 16. 潘金生, 仝健民, 田民波. 材料科学基础[M]. 北京: 清华大学出版社, 1998.
- 17. 林福民. 数学物理方法简明教程[M]. 北京: 北京大学出版社, 2008.
- 18. 胡敏. 扩散方程高精度加权差分格式的MATLAB实现[J]. 四川文理学院学报, 2014, 24(5):15-18.
- 19. 常旭, 石伟. 基于 MATLAB 的渗氮扩散数值模拟程序[J]. 热处理技术与装备, 2015, 36(5): 9-15.
- 20. Boltzmann, L. (1894) Zur Integration der Diffusionsgleichung bei variabeln Diffusionscoefficienten. Wiedemann’s Annalen, 53, 959-964.
- 21. Matano, C. (1933) On the Relation between the Diffusion-Coefficients and Concentrations of Solid Metals (The Nickel-Copper System). Japanese Journal of Physics, 8, 109-113.
- 22. Chen, J., Zhang, C., Wang, J., et al. (2015) Thermodynamic Description, Diffusivities and Atomic Mobilities in Binary Ni-Os System. Calphad, 50, 118-125. https://doi.org/10.1016/j.calphad.2015.06.001
- 23. Kirkaldy, J.S. (1957) Diffusion in Multicomponent Metallic Systems. Canadian Journal of Physics, 35, 435-440. https://doi.org/10.1139/p57-047
- 24. 王常珍. 冶金物理化学研究方法[J]. 北京: 冶金工业出版杜, 1982: 307.
- 25. 杨绮琴, 刘冠昆. 金属在其合金相中扩散系数的测定[J]. 稀有金属, 1992, 16(1): 18-21.
- 26. 赵长伟, 马沛生, 何明霞. 液相扩散系数测定方法的近期研究进展[J]. 化学工业与工程, 2002, 19(5): 374-379.
- 27. 吴永炘, 文效忠, 杨志雄, 等. 镀层中基体金属扩散系数的测定[J]. 电镀与涂饰, 1999(4): 008.
- 28. Brown, R. (1828) A Brief Ac-count of Microscopical Observations Made in the Months of June, July and August 1827, on the Particles Contained in the Pollen of Plants, and on the General Existence of Active Molecules in Organic and Inorganic Bodies. Philosophical Magazine Series 2, 4, 161-173. https://doi.org/10.1080/14786442808674769
- 29. Mehrer, H. and Stolwijk, N.A. (2009) Heroes and Highlights in the History of Diffusion. Diffusion Fundamentals, 11, 1-32.
- 30. Narasimhan, T.N. (2009) The Dichotomous History of Diffusion. Physics Today, 62, 48-53.
- 31. Einstein, A. (1905) Über die von der molekularkinetischen Theorie der Wärmegeforderte Bewegung von in ruhenden Flussigkeitensuspendierten Teilchen. Annalen der Physik, 322, 549-560. https://doi.org/10.1002/andp.19053220806
- 32. Von Smoluchowski, M. (1906) Zurkinetischentheorie der brownschenmolekularbewegung und der suspensionen. Annalen der Physik, 326, 756-780. https://doi.org/10.1002/andp.19063261405
- 33. Perrin, J. (1908) La loi de Stokes et le mouvementbrownien. Comptesrendus, 147, 475-476.
- 34. Groh, J. (1920) Die Selbstdiffusionsgeschwindigkeit des geschmolzenen Bleis. Annalen der Physik, 368, 85-92. https://doi.org/10.1002/andp.19203681705
- 35. Groh, J. (1921) Die Selbstdiffusion in festem Blei. Annalen der Physik, 370, 216-222. https://doi.org/10.1002/andp.19213701103
- 36. Kirkendall, T.D., Thomassen, L. and Upthegrove, C. (1939) Rates of Diffusion of Copper and Zinc in Alpha Brass. Transaction of American Institute of Mining, Metallurgical, and Petro-leum Engineers, 133, 186-203.
- 37. Darken, L.S. (2010) Diffusion, Mobility and Their Interrelation through Free En-ergy in Binary Metallic Systems. Metallurgical and Materials Transactions A, 41, 545-555.
- 38. Le Claire, A.D. (1951) Grain Boundary Diffusion in Metals. The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, 42, 468-474. https://doi.org/10.1080/14786445108561177
- 39. Fisher, J.C. (1951) Calculation of Diffusion Penetration Curves for Surface and Grain Boundary Diffusion. Journal of Applied Physics, 22, 74-77. https://doi.org/10.1063/1.1699825
- 40. Hoffman, R.E. and Turnbull, D. (1951) Lattice and Grain Boundary Self-Diffusion in Silver. Journal of Applied Physics, 22, 634-639. https://doi.org/10.1063/1.1700021
- 41. Viljoen, E.C., Du Plessis, J., Swart, H.C. and van Wyk, G.N. (1995) Sn Bulk-to-Surface Diffusion in a Cu (111)(Sn) Single Crystal. Surface Science, 342, 1-10. https://doi.org/10.1016/0039-6028(95)00684-2
- 42. Wang, J.Y., Du Plessis, J., Terblans, J.J. and van Wyk, G.N. (1999) Kinetics near the Discontinuous Surface Transition in the Cu (Ag)(111) Binary Segregating System. Surface Science, 423, 12-18. https://doi.org/10.1016/S0039-6028(98)00819-X
- 43. Wang, J.Y., Du Plessis, J., Terblans, J.J. and van Wyk, G.N. (1999) The Discontinuous Surface Transition in the Cu (111)(Ag) Binary Segregating System. Surface Science, 419, 197-206. https://doi.org/10.1016/S0039-6028(98)00790-0
- 44. Laughlin, D. and Cahn, J. (1975) Spinodal Decompo-sition in Age Hardening Copper-Titanium Alloys. Acta Metallurgica, 23, 329-339. https://doi.org/10.1016/0001-6160(75)90125-X
- 45. 胡赓祥, 等编著. 材料科学基础(第三版) [M]. 上海: 上海交通大学出版社, 2010.
- 46. Thornton, J. and Hoffman, D. (1989) Stress-Related Effects in Thin Films. Thin Solid Films, 171, 5-31. https://doi.org/10.1016/0040-6090(89)90030-8
- 47. 邵珊珊. 力及力–电耦合作用下微结构中扩散, 应力和变形分析[D]: [博士学位论文]. 上海: 华东理工大学, 2011.
- 48. Prussin, S. (1961) Generation and Distribution of Disloca-tions by Solute Diffusion. Journal of Applied Physics, 32, 1876-1881. https://doi.org/10.1063/1.1728256
- 49. Li, J.C.M. (1978) Physical Chemistry of Some Microstructural Phenomena. Metallurgical Transactions A, 9, 1353- 1380. https://doi.org/10.1007/BF02661808
- 50. Larche, F. and Cahn, J.W. (1973) A Linear Theory of Thermochemical of Solids under Stress. Acta Metallurgica, 21, 1051-1063. https://doi.org/10.1016/0001-6160(73)90021-7
- 51. Larch, F. and Cahn, J.W. (1978) A Nonlinear Theory of Thermochemical Equilibrium of Solids under Stress. Acta Metallurgica, 26, 53-60. https://doi.org/10.1016/0001-6160(78)90201-8
- 52. Larche, F.C. and Cahn, J.W. (1978) Thermochemical Equilibrium of Multiphase Solids under Stress. Acta Metallurgica, 26, 1579-1589. https://doi.org/10.1016/0001-6160(78)90067-6
- 53. Larche, F.C. and Cahn, J.W. (1982) The Effect of Self-Stress on Diffusion in Solids. Acta Metallurgica, 30, 1835- 1845. https://doi.org/10.1016/0001-6160(82)90023-2
- 54. 杨小斌, 涂善东. 碳扩散和扩散应力的相互影响分析[J]. 固体力学学报, 2013(S1): 74-78.
- 55. Gao, H., Zhang, L., Nix, W.D., Thompson, C.V. and Arzt, E. (1999) Crack-Like Grain-Boundary Diffusion Wedges in Thin Metal Films. Acta Materialia, 47, 2865-2878. http://dx.doi.org/10.1016/S1359-6454(99)00178-0
- 56. Zhang, L. (2000) A Class of Strongly Coupled Elasticity and Diffusion Problems in Thin Metal Films. Stanford University, Stanford.
- 57. Chateau, J.P., Delafosse, D. and Magnin, T. (2002) Numerical Simulations of Hydrogen-Dislocation Interactions in Fcc Stainless Steels, Part II: Hydrogen Effects on Crack Tip Plasticity at a Stress Corrosion Crack. Acta Materialia, 50, 1523-1538. https://doi.org/10.1016/S1359-6454(02)00009-5
- 58. Klinger, L. and Rabkin, E. (2011) Theory of the Kirkendall Effect during Grain Boundary Interdiffusion. Acta Materialia, 59, 1389-1399. https://doi.org/10.1016/j.actamat.2010.10.070
- 59. Chen, Y.C., Zhang, Y.G. and Chen, C.Q. (2004) General Theory of Interdiffusion Growth in Diffusion Couples. Materials Science and Engineering A, 368, 1-9. https://doi.org/10.1016/S0921-5093(03)00480-5
- 60. 陈永翀. 扩散蠕变理论的基础问题研究[J]. 稀有金属, 2012, 36(2): 171.
- 61. 陈永翀, 其鲁, 张永刚, 等. 固体互扩散生长的唯象理论[J]. 北京大学学报(自然科学版), 2006, 42(2): 168-174.
- 62. 陈永翀, 其鲁, 张永刚, 等. 固态反应周期层片型结构分析[J]. 金属学报, 2005, 41(3): 235-241.
- 63. Chen, Y., Zhang, Y. and Chen, C. (2003) Quantitative Descriptions of Periodic Layer Formation during Solid State Reactions. Materials Science and Engineering A, 362, 135-144. https://doi.org/10.1016/S0921-5093(03)00479-9
- 64. Chakraborty, J. (2005) Diffusion in Stressed Thin Films. Uni-versitat Stuttgart, Stuttgart.
- 65. Galdikas, A. and Moskalioviene, T. (2010) Stress Induced Nitrogen Diffusion during Nitriding of Austenitic Stainless Steel. Computational Materials Science, 50, 796-799. https://doi.org/10.1016/j.commatsci.2010.10.018
- 66. Galdikas, A. and Moskalioviene, T. (2011) Modeling of Stress Induced Nitrogen Diffusion in Nitrided Stainless Steel. Surface and Coatings Technology, 205, 3742-3746. https://doi.org/10.1016/j.surfcoat.2011.01.040
- 67. Moskalioviene, T. and Galdikas, A. (2012) Stress Induced and Concentration Dependent Diffusion of Nitrogen in Plasma Nitrided Austenitic Stainlesssteel. Vacuum, 86, 1552-1557. https://doi.org/10.1016/j.vacuum.2012.03.026
- 68. Onsager, L. (1945) Theories and Problems of Liquid Diffusion. Annals of the New York Academy of Sciences, 46, 241- 265. https://doi.org/10.1111/j.1749-6632.1945.tb36170.x
- 69. Christiansen, T. and Somers, M.A.J. (2006) Avoiding Ghost Stress on Reconstruction of Stress-and Composition- Depth Profiles from Destructive X-Ray Diffraction Depth Profiling. Materials Science and Engineering A, 424, 181- 189. https://doi.org/10.1016/j.msea.2006.03.007
- 70. Hoeft, D., Latella, B.A. and Short, K.T. (2005) Residual Stress and Cracking in Expanded Austenite Layers. Journal of Physics: Condensed Matter, 17, 3547-3558. https://doi.org/10.1088/0953-8984/17/23/007
- 71. Christiansen, T.L. and Somers, M.A.J. (2009) Stress and Composition of Carbon Stabilized Expanded Austenite on Stainless Steel. Metallurgical and Materials Transactions A, 40, 1791-1798. https://doi.org/10.1007/s11661-008-9717-9
- 72. 关振铎, 等编著. 无机材料物理性能[M]. 北京: 清华大学出版社, 1992.
- 73. Larche, F. and Cahn, J. (1985) The Interaction of Composition and Stress in Crystalline Solids. Acta Met-allurgica, 33, 331-357. https://doi.org/10.1016/0001-6160(85)90077-X
- 74. Klinger, L. and Rabkin, E. (2011) Grain Boundary Interdiffusion and Stresses in Thin Polycrystalline Films. Journal of Materials Science, 46, 4343-4348. https://doi.org/10.1007/s10853-010-5237-2