Computer Science and Application
Vol.08 No.03(2018), Article ID:24275,12
pages
10.12677/CSA.2018.83040
Research on the Parallelization of Bezier Curve Generation Algorithm Based on CUDA
Zhihong Liang1, Fei Dai1*, Peng Cao2, Yuxiang Huang2, Mingming Qin1
1School of Big Data and Intelligent Engineering, Southwest Forestry University, Kunming Yunnan
2School of Software Engineering, Yunnan University, Kunming Yunnan
Received: Mar. 10th, 2018; accepted: Mar. 22nd, 2018; published: Mar. 29th, 2018

ABSTRACT
The Bezier curve is essential for geometric modeling system and graphic software. A method of calculating Bezier curve based on CUDA is proposed. Based on the analysis of the CUDA isomeric computing architecture and the independence of the Bezier curve sampling points, the multiple threads were opened on the GPU to calculate the Bezier curve. According to the characteristic that the control vertex does not change during the calculation of the sampling point, the calculation of the sampling point was optimized at the memory level. The experimental results show that the performance of Bezier curve generation algorithm based on CUDA has been improved remarkably.
Keywords:GPU, Bezier Curve, CUDA
基于CUDA的Bezier曲线生成算法并行化研究
梁志宏1,代飞1*,曹鹏2,黄宇翔2,秦明明1
1西南林业大学大数据与智能工程学院,云南 昆明
2云南大学软件学院,云南 昆明

收稿日期:2018年3月10日;录用日期:2018年3月22日;发布日期:2018年3月29日

摘 要
针对Bezier曲线在几何造型系统和图形软件中的重要作用,提出了一种基于CUDA的对Bezier曲线进行计算的方法。在分析CUDA异构计算架构和Bezier曲线采样点计算独立性的基础上,在GPU上开启多线程对Bezier曲线进行计算。并根据控制顶点在采样点计算过程中不改变的特性,在存储器层次对采样点的计算进行优化。实验结果表明,基于CUDA改进后的Bezier曲线生成算法性能有了显著的提高。
关键词 :GPU,Bezier曲线,CUDA

Copyright © 2018 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 概述
当今社会是一个数据爆炸的社会,也是一个人工智能的时代。为了处理大量的数据以及为了满足人工智能算法的处理能力的要求,无论是工业界还是学术界都进行了长远探索。超级计算机、计算机集群、以及专用神经网络芯片如TPU、寒武纪等都是人们对计算能力需求探索的成果。无论是超级计算机、计算机集群,还是专用芯片,虽然它们可以满足人们对计算能力的要求,但是缺点也同样明显。例如系统造价以及维护费用昂贵,而且能耗也相当惊人,此外还有价格也比较贵,编程复杂,学习曲线比较陡峭。专用芯片还有功能比较固定,往往只能满足人们对某一个特定类型的计算的需求的缺点。因此上述三种解决方面都不适合个人以及小型实验室使用。在可以满足一定计算能力的前提下,又要克服上述系统的缺点,GPU-CPU异构计算 [1] 无疑成为了人们首要的选择,而在GPU-CPU异构的计算方面NVIDA发布的CUDA编程模型 [2] 凭借着在通用性、可编程性、以及计算能力方面的优势无疑成为了业界的领导者。因此基于CUDA的应用研究已经成为了当今学术界与产业界研究的热点。例如,在医学图像领域,为了更好诊断乳腺癌,人们研发了TechniSan医疗系统。TechniSan [3] 采用了一种三维的超声波成像方法,在TechniSan医疗系统刚研发出来时,由于超声波数据转换为3D图像时需要执行非常耗时的计算,因此这项技术一直无法投入实际应用。由于CUDA的出现,人们采用两个NVIDIA Tesla C1060来处理在15分钟扫描过程中产生的35G数据。得益于GPU的大规模数据的处理能力,医生可以在20分钟内就可以得到患者高清三维成像。美国天普大学的研究者使用GPU对HOOMD (Highly Optimized Object-Oriented Many-Particle Dynamics) [4] 模拟软件进行加速,HOOMD将模拟实验任务分解到两个NVIDIA Tesla GPU,HOOMD实现的表面活性剂交互模拟性能是之前没有使用GPU加速的16倍。在数据库方面,Govindaraju等 [5] 在Geforce 6800 GPU上实现了数据库的一些基本操作,这些操作包括合取选择、聚合、查询等。在GPU上的数据库操作比在2.8 GHz的Intel Xeon处理器上快了近一个数量级。在国内很多研究者也对基于GPU的应用进行了大量的研究,例如朱鉴等 [6] 提出了基于GPU加速的实时图像绘制算法。杨正龙等人 [7] 提出了一种基于GPU的加速目标电子多次散射的计算的算法,获得了大约20倍的性能提升。而陈波等 [8] 在前人的基础上运用CUDA异构编程平台,提出了基于CUDA的对基因序列对比进行加速,通过GPU加速后的算法比之前的算法快了60多倍。
在1962年,法国雷诺汽车公司的工程师P. E Bézier提出了一种以逼近为基础的参数曲线的构造方法 [9] [10] [11] ,这种由Bézier提出的构造曲线的方法所构造的曲线称为Bézier曲线。Bézier曲线在1972年在用于汽车表面设计的UNISURF系统中得到应用。Bézier方法是一种将函数逼近同几何表示结合起来的方法。自从Bézier方法被提出之后,设计师在计算机上作图就像使用作图工具一样方便,且容易修改。后来Bézier曲线广泛的应用于很多图形图像软件中,例如Flash、IIIstrator、CoraIDRAW和Photoshop等。在工程设计中,单独的Bézier曲线不能满足产品设计的要求,因此需要对Bézier曲线进行拼接。因此就需要计算多条曲线,但是曲线的计算是一种计算量比较大的算,单条曲线的计算很容易完成,但是在设计系统中,要计算曲线的条数是非常大的,因此本文在分析Bézier生成算法的基础上,对其进行并行化,并在GPU进行曲线的生成的计算。
2. CUDA编程模型
2.1. CUDA概述
CUDA [12] 是NVIDIA公司在2007年提出的一种基于本公司GPU的可以进行通用计算并且编程性较好的编程模型,是一种利用GPU与CPU协同进行计算的编程模型。在CUDA中,CPU被称作主机,GPU被称作设备。为了使开发者可以更快的使用CUDA编程平台进行开发,CUDA的编程语言采用了扩展后的类C语言—CUDA C。使用CUDA C可以直接编写可以运行在GPU上的程序而不需要懂得OpenGL或者Direct3D等API [13] 。在NVIDIA的官方文档CUDA C Programming Guide Version 7.5中,CUDA的核心主要在三个抽象概念:线程组层次结构(a hierarchy of thread groups),共享内存(shared memories),障栅同步(barrier synchronization) [3] 。正是由于这些抽象,CUDA可以提供细粒度的线程并行和数据并行。较细粒度的并行线程组成线程块 [3] ,从而使CUDA可以提供粗粒度的任务并行和数据并行。正是由于这些抽象,程序员可以把一些大的计算任务进行数据划分,划分成无数小的数据集合,每个线程对一个小数据集合进行处理,从而提高程序的运行效率。
2.2. CUDA的软件体系结构
CUDA的软件栈是按照层次结构来组织的,如图1所示。CUDA为开发者提供了一套夸平台的支撑软件来方便程序员更加容易和灵活的开发CUDA程序。如图1所示CUDA的软件层次是:CUDA函数库,CUDA运行时API,CUDA驱动API。CUDA库函数是NVIDIA已经写好的一些函数,程序员可以在应用程序中直接调用,从而节约开发时间。而CUDA运行时API和CUDA驱动API实现GPU内存的分配以及核函数 [3] 的启动等一些GPU资源管理的函数接口。
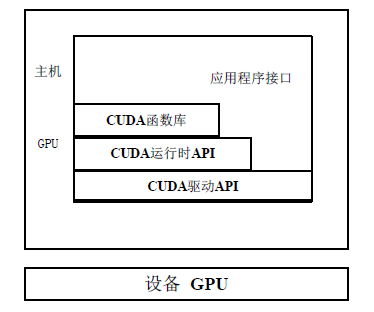
Figure 1. CUDA software architecture diagram
图1. CUDA软件架构图
CUDA应用程序代码包含两部分:一部分是运行在GPU上的设备代码 [10] ,一部分是运行在CPU上的主机代码 [14] 。NVCC (NVIDIA C Compiler) [2] 在编译CUDA应用程序时,如图2所示。NVCC根据CUDA关键字把设备代码和主机代码区分开来。NVCC把这部分主机代码(用ANSI C编写的简单代码)发送到标准C或者C++编译器进一步编译,编译后以一个普通的CPU进行的方式进行运行。而用CUDA关键字标记的设备代码通常再由NVCC编译器进一步编译,并在GPU上运行。
在GPU运行的代码是并行代码,运行这些并行代码的实体是在启动CUDA程序时配置的CUDA线程。在启动核函数时,会产生无数的线程来执行这些并行的代码。CUDA将串行的事物处理,如初始化GPU设备、准备数据、分配显存、主机与设备间数据传输等操作放在GPU上运行。而一些需要大量线程实现来对数据进行计算的并行任务放在GPU上运行。
2.3. CUDA的硬件体系架构
在支持CUDA的GPU中,GPU本质上是一个线程处理器群TPC [1] (Thread Processing Cluster),TCP的核心是流多处理器SM [1] (Streaming Multiprocessor)。由若干个SM组成GPU,不同的设备所包含的SM数量不同。每个SM由若干个SP (Streaming Processor) [2] 组成,每个流处理器SP拥有独立的寄存器和指令指针,并且拥有自己私有的一组32位的寄存器,但是没有取指和调度单元。在一个SM中的所有SP共用一套取指和发射单元,常量缓存、纹理缓存以及共享内存也是SM中所有的SP所共享的。SM是一个完整的核心,拥有完成的前端,包括取指、译码、发送指令、执行单元等,所以SM可以完成线程的创建、调度,而线程的执行由SP完成。一个SM类似于CPU中的一个核。
2.4. CUDA的执行模型
CUDA异构编程架构的硬件由两部分组成,一部分是CPU,也称作主机 [2] (Host),另一部分是是协处理器(co-processor) GPU,也称作是设备。在CUDA异构系统中可以由一个主机和若干个GPU搭配组成。正如前面我们提到的GPU与CPU各有分工,相互合作。计算量比较小的串行计算和逻辑比较复杂的事务性处理都放在CPU上运行,而运算量比较大,数据依赖性比较小的大规模数据处理放在GPU上运行。运行在GPU上的代码叫做设备代码,也成为内核函数(kernel) [2] 。运行在CPU上的代码成为主机代码。通过主机端调用核函数,那么再设备上就会有大量的线程实体来执行核函数代码。为了管理大量

Figure 2. CUDA C compilation process diagram
图2. CUDA C编译过程图
的运行在GPU上的线程,CUDA采用了层次结构来管理这些线程。CUDA把运行在GPU上大量的相处划分成维度和大小都相同的线程块(Block),这些线程块再按照一定的方式排列成线程网格(Grid)。
在CUDA的线程网格中,每个线程块都有一个唯一的标识线程块ID,在线程块中为了标识每一个线程,每个线程都有一个唯一的线程ID。标识线程块ID的内置变量是blockIdx,而标识线程ID的内置变量是threadIdx。运行在GPU上的所有线程组成了线程网格,线程网格grid可以是一维的,也可以二维的,也可以是三维的,同样的组成线程网格的线程块也可以是一维、二维或者三维。而用来表示线程网格维度的内置变量是gridDim,用来表示线程块维度的内置变量是blockDim。gridDim,blockDim,blockIdx,threadIdx这四个内置变量的类型都是CUDA中定义的一个新的数据类型dim3。其实dim3这个数据是由uint3实现的一个结构体。在启动核函数时,会在GPU上产生相应的线程来执行并行代码,线程的数量是由<<<>>>语法来指定的。例如一个核函数testKernal<<<32,128>>>(…)被调用,那么再GPU上就会启动32 × 128个线程,其中32是线程网格中线程块的数量,128是线程块中线程网格的数量。在GPU执行的线程块还会被划分成一个逻辑单位叫线程束(warp),每个线程束一般是32个线程组成,warp是CUDA中的最小执行单位。
2.5. CUDA的存储器模型
GPU的存储器的种类以及层次相比于CPU会非常的复杂,每一种存储器的存取速度以及存储容量都不一样。GPU的存储器包括寄存器存、局部存储器、全局存储器、常量存储器、纹理存储器、共享内存等。在线程网格中,每个线程根据自己的情况所能访问的存储器也不同。在图3中,可以看出每个线
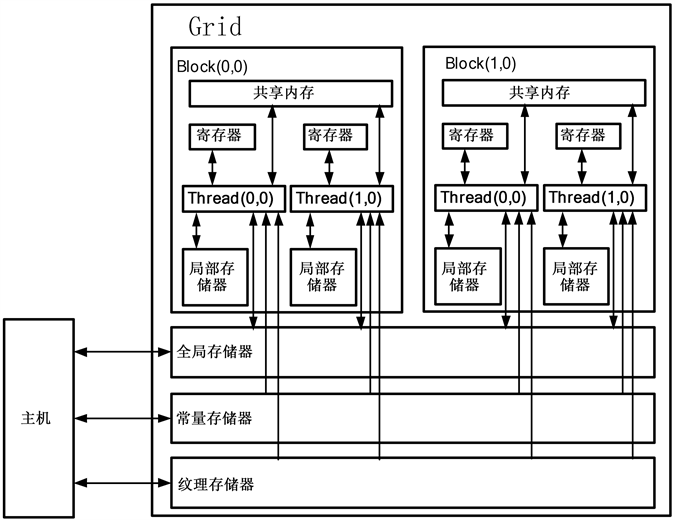
Figure 3. Memory hierarchy diagram
图3. 存储器层次图
程都有私有的寄存器和局部内存。每个线程块都有一块供线程块内所有线程所共享的共享存储器。在线程网格中的所有线程都可以访问全局内存即显存。另外还有两个对线程网格中所有线程都可以访问的只读存储器:常量内存和纹理内存。
3. Bézier曲线相关理论
在1962年,Pierre Bézier以逼近理论为基础,第一次提出了Bézier曲线曲面 [10] [11] ,并给出了相应的计算公式。贝塞尔给出构造Bézier曲线的公式是基于贝塞尔基函数的,在当时贝塞尔并未给出公式的证明,所示很多人难以理解贝塞尔提出的这种曲线理论。一直到1972年,剑桥大学的博士生Forrest在《Computer Aided Design》发了一篇论文,证明了贝塞尔曲线实际上是可以由控制定点和伯恩斯坦基多项式函数的线性组合构成。在1980年,我国的施法中等 [15] 在《航空学报》中给出了贝塞尔基函数的导出的证明。
3.1. Bézier曲线的定义
定义(2.1):给定空间n + 1个点的位置矢量 ,则Bezier曲线段的参数方程表示如下:
[10] [11] (2.1)
其中 是控制多边形的n + 1个顶点,即构成曲线的特征多边形或者称为控制多边形, 称为控制定点。Bi,n(t)是伯恩斯坦多项式,其形式如下:
[10] [11] (2.2)
在图4中展示了3阶4个顶点的Bézier曲线。
3.2. Bézier曲线的性质
在公式(2.1)中可以看到,贝塞尔曲线是由控制定点和伯恩斯坦基函数线性组合生成的,那么伯恩斯坦多项式的性质就决定了贝塞尔曲线的性质。因此贝塞尔曲线具有如下性质:
1) 端点性质。
Bézier曲线的起点和终点与控制多边形的起点和终点重合。
2) 切矢量。
Bézier曲线的起点处的切线方向与特征多边形的第一条边走向一样,终点处的切线方向和特征多边形最后一条边走向一样。
3) 对称性。
由控制顶点 ,构造出的新的Bézier曲线与原Bézier曲线形状相同,但走向相反。

Figure 4. Three order Bessel curve
图4. 三阶贝塞尔曲线图
4) 凸包性。
在几何图形上,这就表示Bézier曲线P(t)在 上,落在 构成的凸多变形中。
5) 几何不变性。
因为采取的是参数方程来表示Bézier曲线,所以具有几何不变性,即一些几何特性不随坐标的变换而变化的特性。
6) 变差缩减性。
若Bézier曲线的特征多边形是一个平面图形,则平面内任意直线与p(t)的交点个数不多于该直线与其特征多边形的交点个数,这一性质叫变差缩减性质。此性质反映了Bézier曲线比其特征多边形的波动还小,也就是说Bézier曲线比特征多边形的折线更光顺。
4. 基于CUDA的Bézier曲线生成算的设计与实现
在几何造型系统中进行复杂设计时需要无数条曲线对要设计的产品进行刻画,为了让人们看到的由设计软件画出的曲线是连续的、不间断的,就必须在用离散的点刻画曲线时采用足够多的采样点。为了让人们看到的曲线是连续的,就需要进行大量的计算,而采用传统的CPU进行Bézier曲线生产算法的计算芯片,无疑会使得曲线生成的时间很长。那么在造型系统中,要设计无数的曲线,采用CPU串行的算法所需要的时间无疑是巨大的,这就严重影响整个造型系统的运行速度,从而为人们设计产品带来了不便。因为GPU有强大的计算能力,并且具有天然的并行优势,所以采用GPU来对Bézier曲线生成算法进行并行化具有一定的意义。
4.1. 基于CUDA的Bézier曲线生成算法的描述
在串行算法中,根据公式(2.1)进行Bézier曲线上采样点的计算时,要求的每个采样点之间是没有依赖关系的。所有的采样点计算都依赖于两部分:一是输入的Bézier曲线控制顶点,二是Bézier曲线控制顶点前面的Bernstein基函数的值。例如我们用513个点来刻画一条Bézier曲线,那么再串行算法中就是每次计算一个采样点,需要做一个513次的循环,每次循环根据公式(2.1)与公式(2.2)来计算一个Bézier曲线的采样点。在公式(2.2)中有一个变量t,t值的计算和采样点的需要有关系。例如一个Bézier曲线是由513个采样点进行刻画,那么当第一个采样点对应的t值就是0/512,第二个采样点对应的t值就是1/512,依次类推,最后一个采样对应的采样点的t值就是512/512。按照这种方法所得到的t值就满足在区间[0, 1]上。
在前面描述的串行算法中,可以看到在计算Bézier曲线上的采样点时是通过循环,并且各个采样点之间并没有依赖关系。因此采样点的计算可以并行化,即采样点的计算可以通过多线程同时进行。所以我们可以把对采样点求值的串行循环部分进行展开,对采样点的计算并行化。
并行算法思想的描述:
1) 在设备上分配用于存储控制顶点以及曲线采样点的设备内存。输入控制顶点以及控制顶点数m,
2) 输入采样点的数N,N的值要是32的整数倍
3) 把控制定点的数据以及计算出的二项式系数传输到设备
4) 启动核函数,启动N/32个线程块,每个线程块32个线程
5) 根据线程块的blockIdx.x以及线程的threadIdx.x,还有blockDim.x来计算每个线程的序号,每个线程的序号就是要计算的采样点的序号。设线程的序号tid=threadIdx.x+blockIdx.x*blockDim.x
6) 根据计算的tid来计算以及N的值按照t=(tid/N)来计算t的值
7) 根据t的值以及控制顶点的坐标对Bézier曲线上的所有采样点同时进行计算
8) 把计算好的采样点坐标值传输回主机
9) 释放设备端分配的内存
在上述算法的描述中步骤(5)、(6)、(7)都是运行在GPU上的。在GPU上运行的示意图如图5所示。
在图5中,在GPU上开辟N个线程,T0, T1, T2, ∙∙∙, Tn-2, Tn-1就是GPU上开启的线程,每个线程计算Bézier曲线上的一个采样点,并把计算完的采样点存入相应的设备内存中。
4.2. 基于CUDA的Bézier曲线生成算法的实现
根据4.1节中的对Bézier曲线生成算法的描述,我们知道对Bézier曲线上采样点的计算进行化。在本节我们给出算法的核心部分。
1) 数据结构设计
每一个点用一个结构体进行表示,因此我们定义结构体Point来表示一个点结构体定义如下:
typedef struct Point{//结构体Point用于存放点
float x;
float y;
}Point;
2) 设备内存分配
对采样点进行计算的输入时控制顶点,控制顶点在计算过程中是只读的。因此未来在计算采样点时对控制顶点的读取更快,把控制顶点的值放在设备上的常量内存,设备上常量内存的定义在主机端进行定义,定义形式如下:
如果想要把主机内存的数据传输到设备的常量内存,必须要用特殊的主机设备传输函数cudaMemcpyToSymbol(destAdd,srcAdd,size);,在cudaMemcpyToSymbol()函数中有三个参数,第一个参数destAdd代表目的地址,srcAdd代表源地址,size代表要传输的数据的大小,单位是字节。所以输入控制顶点的代码以及二项式系数的代码如下:
cudaMemcpyToSymbol(dev_cltpoints,host_ctlpoints,sizeof(Point)*M);
cudaMemcpyToSymbol(dev_bin,host_bin,sizeof(float)*M);
除了上述的控制顶点,还需要在设备中分配输出缓存用来存储求出的采样点的坐标,因为需要对输

Figure 5. GPU calculation sample point diagram
图5. GPU计算采样点简图
出缓存进行写操作,因此不能声明为constant内存。所以需要把输出缓存放在全局设备内存中,分配代码如下:
cudaMalloc((void**)dev_points,sizeof(Point)*N);
cudaMemset(dev_points,0,N*sizeof(Point));//把分配的设备内存初始化为0
3) 二项式的计算
在公式(2.2)中有一个 的计算,其中n代表Bézier曲线的阶数,i代表控制顶点的序号,
且 。设置一个设备函数__device__ int computeBin(int n,int i)来计算每个采样点前的二项式的值。

4) Bézier曲线上采样点的计算
在做完分配好内存,传输数据后的准备工作后,便可以来计算Bézier曲线上的采样点了,其计算函数的代码如下:

启动内核函数的代码如下:
computeBezier<<<(N+63)/64,64>>>(dev_points);
5) 最后清理
在计算完所有的采样点坐标后,需要把计算好的坐标从设备内存传输回主机内存,并把分配的空间进行释放。
代码如下:
cudaMemcpy(host_points,dev_points,N*sizeof(Point),cudaMemcpyDeviceToHost);//把计算好的采样点坐标传输回主机缓冲区。
cudaFree(dev_points);//对cudaMalloc()分配的设备内存进行释放。
5. 实验结果以及分析
为了验证基于CUDA的Bézier曲线生成算法的性能,采用3阶Bézier曲线,并对Bézier曲线的采样点数设置成了64、128、256、512、768、1024。一般情况下采样点设置成1024时,生成的曲线就已经比较平顺光滑了。控制顶点的坐标我们选择{−40.0, 0.0}, {−10.0, 30}, {10.0, 30}, {40.0, 0.0}。
1) 实验环境如下:
硬件环境:
CPU:Intel Core i5-4210M双核处理器
GPU:NVIDA GTX850M DDR3独立显卡
主机内存:4 G
显卡内存:2 G
GPU SM数:5
SP/SM:128
GPU SP数:640
设备计算能力:5.0
软件环境:
操作系统:CentOS 6.5
开发平台:CUDA ToolKit 7.5
2) 实验结果
为了更好的分析算法的性能,对改进后的算法运行的时间采用两种计时方式,第一种是在不考虑设备内存分配、主机端与数据端数据传输情况下的GPU的运行时间,第二种是考虑设备内存分配、主机端与数据端数据传输情况下的GPU的运行时间,并给出两种情况下的加速比。运行时间对比图如图6所示。
3) 实验结果分析
从上述的实验结果中我们可以看到当采样点比较少时,Bézier曲线生成算法的加速效果不是很明显,但是随着采样点的越来越多,可以看到运行在CPU上的串行算法所花费的时间增长的特别块,而在GPU上并行的算法所花费的时间几乎没有改变。可以看出明显的加速效果。从这里可以看到GPU特别适合处理这种并行性比较高且生成的数据的依赖性不强的算法。在Bézier曲线生成算法增加了计算的采样点数量,但是在GPU上运行的算法所花费的时间几乎没有改变,原因是我们计算的采样点数量还不够足够大,实验平台上GPU的性能还没有全部被挖掘,即使增加采样点数量,运行时间也几乎没有改变。除非当采样点的数量足够大,让GPU上所有的SM以及SP都忙碌起来,这时运行在GPU上的时间才会随采样点数量的增加而增加。可以看到包含设备内存分配、设备与主机间数据传输的时间会比仅仅在GPU计算采样点的运行时间高出了很多,因此在GPU中同样才存在GPU真正的计算时间在整个算法中所占的比重很小,在整个算法中内存的数据传输以及内存的分配释放占据了整个算法运行时间的大部分。
6. 结束语
本文对Bézier曲线的生成算法进行了分析,识别出在Bézier曲线生成算法中采样点的计算是一种数据依懒性不强且可以并行的过程,把这个并行的过程移植到GPU进行计算。在NVIDIA公司的CUDA编程架构下对并行的算法进行了实现,最后对实验的结果进行了对比分析。在不考虑设备内存的分配与

Figure 6. Run time contrast diagram
图6. 运行时间对比图
主机设备数据传输的情况下,在GPU上实现Bézier曲线生成算法,获得相对CPU上最高100多的加速比,而考虑设备内存的分配与主机设备数据传输的情况下,在GPU上实现Bézier曲线生成算法,获得相对CPU上的加速比也达到了15.
文章引用
梁志宏,代 飞,曹 鹏,黄宇翔,秦明明. 基于CUDA的Bezier曲线生成算法并行化研究
Research on the Parallelization of Bezier Curve Generation Algorithm Based on CUDA[J]. 计算机科学与应用, 2018, 08(03): 354-365. https://doi.org/10.12677/CSA.2018.83040
参考文献
- 1. 白洪涛. 基于GPU的高性能并行算法研究[D]: [博士学位论文]. 长春: 吉林大学, 2010.
- 2. NVIDIA Corporation. (2015) CUDA C Programming Guide Version 7.5.
- 3. Jason Sanders, Edward Kandrot. GPU高性能编程—CUDA实战[M]. 北京: 机械工业出版社, 2011.
- 4. The Regents of the University of Michigan. http://glotzerlab.engin.umich.edu/hoomd-blue/
- 5. Govindaraju, N.K., Lloyd, B., Wang, W., Lin, M. and Manocha, D. (2004) Fast Computation of Database Operations Using Graphics Processors. Proceedings of the ACM SIGMOD International Conference on Management of Data, Paris, 13-18 June 2004, 215-226.
- 6. 朱鉴, 吴恩华. 基于GPU的球面深度图实时绘制[J]. 计算机学报, 2009, 32(2): 231-240.
- 7. 杨正龙, 金林, 李蔚清. 基于GPU的图形电磁计算加速算法[J]. 电子学报, 2007, 35(6): 1056-1060.
- 8. 陈波. 基于CPU-GPU异构平台的性能优化及多核并行编程模型的研究[D]: [硕士学位论文]. 合肥: 中国科学技术大学, 2011.
- 9. 杨钦, 徐永安, 翟红英. 计算机图形学[M]. 北京: 清华大学出版社, 2005.
- 10. 仇茹. Bezier曲线曲面造型技术研究[D]: [硕士学位论文]. 芜湖: 安徽师范大学, 2015.
- 11. 洪玲. 有理Bézier曲线的扩展及应用[D]: [硕士学位论文]. 合肥: 合肥工业大学, 2015.
- 12. Cook, S. (2012) CUDA Programming: A Developer’s Guide to Parallel Computing with GPUs. Publishing house, location, 147-153.
- 13. 侯立华. 图像分割方法综述[J]. 科技创新导报, 2008, 22: 249.
- 14. DavidB. Kirk, Wen-meiW.Hwu. 大规模并行处理器编程实战[M]. 北京: 清华大学出版社, 2013.
- 15. 施法中, 韩道康. Bézier基函数的导出[J]. 航空学报, 1980, 1(1): 92-98.
NOTES
*通讯作者。