Computer Science and Application
Vol.
09
No.
10
(
2019
), Article ID:
32641
,
8
pages
10.12677/CSA.2019.910215
Prediction of Traffic Accident Severity Based on Random Forest and Logistic Regression Model
Xiaogang Guo1, Tong Li2
1School of Software, Yunnan University, Kunming Yunnan
2School of Big Data, Yunnan Agricultural University, Kunming Yunnan

Received: Oct. 2nd, 2019; accepted: Oct. 17th, 2019; published: Oct. 24th, 2019

ABSTRACT
Traffic safety is closely related to people’s lives. The severity of traffic accidents has a great impact on society and people’s lives. This paper chooses random forest and logistic regression algorithm to construct a traffic accident severity prediction model, and makes a prediction and comparative analysis of the severity of traffic accidents. It shows that stochastic forest model has better prediction effect, and ranks the characteristics that affect the severity of traffic accidents. It can judge which factors have greater impact on the severity of traffic accidents. It provides reference and suggestions for traffic road infrastructure construction, as well as for the prevention and reduction of the severity of traffic accidents.
Keywords:Traffic Safety, Traffic Accident Severity, Random Forest, Logistic Regression
基于随机森林与逻辑回归模型的交通事故严重程度的预测研究
郭小刚1,李彤2
1云南大学软件学院,云南 昆明
2云南农业大学大数据学院,云南 昆明

收稿日期:2019年10月2日;录用日期:2019年10月17日;发布日期:2019年10月24日

摘 要
交通安全与人们的生活紧密相关,交通事故造成的严重程度对社会和人们的生活都有极大的影响,本文选取随机森林与逻辑回归算法构建了交通事故严重程度预测模型,对交通事故严重程度进行了预测与对比分析,对比分析显示出随机森林模型有更好的预测效果,并将影响交通事故严重程度的特征进行重要性排序,可以判断哪些因素对交通事故严重程度影响较大,为交通道路基础建设,以及交通事故严重性预防和降低提供了参考与建议。
关键词 :交通安全,交通事故严重程度,随机森林,逻辑回归

Copyright © 2019 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
随着我国经济的讯速发展与道路基础设施建设的不断完善,人民消费水平的逐步提高,车辆出行已经非常普遍,但与此同时,也为交通出行安全带来了较大的风险系数,造成了许多的交通事故。根据2016年国家统计局统计的数据显示,交通事故共发生268,951起,事故造成65,725死亡,受伤人员有198,902,造成的财产损失共计105,692万元。我们的日常生活与交通问题密切相关,交通事故时刻都在发生,交通安全显得尤为重要,并且交通事故的不同严重程度造成的损失相差也是巨大的,轻则小伤,部分财产损失,重则人员伤亡,将会给家庭带来极大的不幸。因此对交通事故的严重程度进行预测和研究,判断交通中的哪些要素会对交通事故严重程度有较大的影响具有重要的意义。
在最近的研究中有很多学者对交通事故领域的问题进行了研究。例如,Ahmed [1] 等通过提取自动车辆识别系统中的交通流数据对实时事故造成的风险进行了研究和分析;Shinohara [2] 等使用了卡方检验分析了车型和安全带对驾驶员和乘客受伤情况的影响;刘攀等研究了极端天气环境对高速公路交通事故的影响;Olutayo V.A. [3] 等使用美国的交通事故数据,分别使用神经网络、决策树、SVM算法来预测交通事故严重程度,并没有对影响交通事故严重程度的影响因素进行描述和分析。鉴于对于交通事故严重程度预测和分析的研究较少,因此本文选择了随机森林和逻辑回归算法对交通事故严重程度进行预测和研究,并且对影响交通事故严重程度的特征重要程度进行了排序。
2. 数据描述与相关变量说明
2.1. 数据的描述
在我国交通信息化还处于起步的发展阶段,正迈向深入地发展,交通事故数据包含大量的个人隐私数据多为国家交通管理部门保管,并没有向社会公开。所以在本文中选取的是国外交通事故数据进行研究,选取的是某国2013~2014年道路交通事故数据,由于数据量比较大,有一些事故数据记录存在缺失的情况,故把这些具有缺失的数据进行删除来进行数据的清洗,然后随机选取14万条交通事故数据。通常情况下造成交通事故的原因有4个方面即环境、车、路和人。该交通事故数据中含有三个表,其中事故表包含环境、天气状况、伤亡人数等因素;车辆表包含车龄、驾驶人年龄等因素;人员伤亡表包含伤亡人年龄,性别等因素。本文利用三张表中的数据用来进行研究。
2.2. 交通事故严重程度的划分
交通事故严重程度的划分标准在每个国家并不唯一,比如在日本,他们把交通事故严重程度划分为轻伤、重伤、死亡三个级别;德国将交通事故严重程度划分为物体损坏、人员受伤较轻、受伤人员较重、有人员死亡这四个等级;而在美国,则将交通事故严重程度划分为无伤事故、轻微伤事故、非致残事故、严重事故、死亡事故五个级别 [4]。在我国交通事故按事故严重程度可以划分为四个等级,分别是无受伤的轻微事故、受伤较轻的事故、有死亡的重大事故、造成多人死亡的特大事故。从以上信息可以看出,虽然每个国家对交通事故严重程度的划分并不相同,但是交通事故严重程度都基本上含有三个级别,即物损轻度事故、受伤中度事故、死亡重度事故。在本文中由于交通事故数据中轻度事故数据较多,中度和重度交事故数据较少,因此将中度和重度交通事故称为严重事故。
2.3. 部分变量说明
在数据中,数据的变量包含事故严重程度、天气状况、灯光条件等,部分变量说明如表1所示。
Table 1. Description of some variables
表1. 部分变量的说明
3. 模型的建立与实验结果分析
3.1. 模型的建立
3.1.1. 随机森林模型
随机森林算法 [5] 是2001年由Breiman L.提出的一种分类方法,该分类模型包含多棵决策树模型。它继承了CART决策树的思想,基于Bagging的集成学习方法,并且运用了特征随机选取的思想 [6]。使用套袋法来构建随机森林。给定自变量X,随机森林分类模型是组合K个决策树分类器 。随机森林分类主要过程:首先在初始样本集中使用套袋法选取K个样本。其次,选择的K个样本将是用于生长K树以实现K分类结果的训练集。最后,K分类器投票以多数票选取最佳分类。
随机森林算法描述:
假定输入训练数据集 ,样本子集的个数为M,输出的结果为最终强分类器 。
(1) 对于
(a) 随机的从原始样本集中抽取t个样本点,得到一个训练集 ;
(b) 使用得到的训练集 训练一个CART决策树,在训练时每个节点的切分是在所有特征中随机选择K个特征,然后在这K个特征中选择最佳分割点来划分左右子树。
(2) 对于分类算法中,最终预测类别是样本点所属叶节点处投票最多的类别;对于回归算法,最终类别是样本点所属的叶节点的平均值。
随机森林算法的优点:
(1) 在处理数据量较大的样本时高度并行化,训练速度较快。
(2) 随机森林运用集成算法,因此准确性比单个算法高。
(3) 对训练样本有很好的适应能力,可以处理维度较高的数据,也可以处理离散型和连续型数据。
(4) 随机森林使用了随机采样,可以明显改善决策树过拟合问题。
3.1.2. 逻辑回归模型
逻辑回归算法是机器学习分类算法中的一种,是广义线性回归模型 [7]。该算法常用于二分类或多分类问题。在数据挖掘、经济预测、医疗疾病的自动诊断等领域经常会被应用 [8]。
假定自变量X与因变量Y,逻辑回归用来描述因变量Y与自变量X的关系,最后预测因变量Y。具体步骤如下:
(1) 首先需要找一个合适的预测函数,表示为h函数,该函数是我们要找的分类函数,也是预测输入数据的判断结果 [9]。利用Sigmoid函数和线性回归函数可以得出h函数。
Sigmoid函数:
(1)
线性回归函数公式为:
(2)
利用(1)与(2)式可以得到h函数如下:
(3)
(2) 构建能够描述模型预测值 与真实值y之间的偏差函数 ,称为代价函数。代价函数求平均值记作 ,一个模型的优劣可以通过 来行判断,当 函数越小,表明当前模型与参数更适合训练样本。基于最大似然估计可以达到 :
(4)
(3) 求 的最小值使用梯度下降法,使用梯度下降法来求最小值是常用的方法。各个参数的偏导数就是 的梯度,机器学习的过程中参数下降的方向就是偏导数的方向,学习率用 表示,通过偏导数使用梯度下降法求出使 最小的 ,在对参数进行更新。推导后可得出 如下:
(5)
3.2. 度量指标
本文中使用准确率、F1-measure、AUC值等指标来评价分类器的性能。
(1) 准确率
在分类任务中最常用的性能度量指标是准确率,它的含义是正确分类的样本数占总样本数的比例,公式如下:
(6)
(2) AUC是ROC曲线下的面积,AUC的值是一个概率值,当AUC的值越大,则表示当前的分类模型拥有更好的分类能力。
(3) F1-measure是查准率和查全率的加权调和平均数,对于一些非平衡的数据集,难以估计小类样本对预测结果的影响,因此通过查准率和查全率能够够有很好的评价。F1-measure计算公式如下:
(7)
其中P是查准率,R是查全率。
3.3. 实验结果与对比分析
3.3.1. 实验结果
在实验的过程中将交通事故严重程度等级中的中度事故与重度事故归为一类为严重事故,将严重故事称为“好样本”,轻度事故称为“坏样本”,把选取的交通事故数据集分为训练集和测试集,在总的数据集中训练数据占比70%,剩余的数据用来进行测试。用训练数据集分别训练随机森林和逻辑回归模型,然后在测试集上进行测试。
随机森林模型对交通事故严重程度预测的准确率为0.75,F1-measure值为0.72。它的ROC曲线如图1所示。

Figure 1. Random forest model ROC curve
图1. 随机森林模型 ROC曲线图
根据随机森林模型得到特征的重要性,并对特征的重要程度进行了排序如表2所示。
Table 2. Importance of features
表2. 特征的重要性
从特征重要性表中,可以知道限速、事故发生地点、天气状况、事故发生的时间、光照条件等对交通事故严重程度都有重要的影响。
在逻辑回归模型中,选取特征重要性较大的属性进行实验。逻辑回归模型对交通事故严重程度预测的准确率为0.71,F1-measure值为0.70。它的ROC曲线如图2所示。

Figure 2. Logistic regression model ROC curve
图2. 逻辑回归模型 ROC曲线图
3.3.2. 对比分析
随机森林模型与逻辑回归模型预测准确率与F1-measure对比结果如表3。
从表中可以看出:
Table 3. Comparison of the two models
表3. 两种模型对比结果
随机森林模型与逻辑回归模型ROC曲线对比如图3所示。
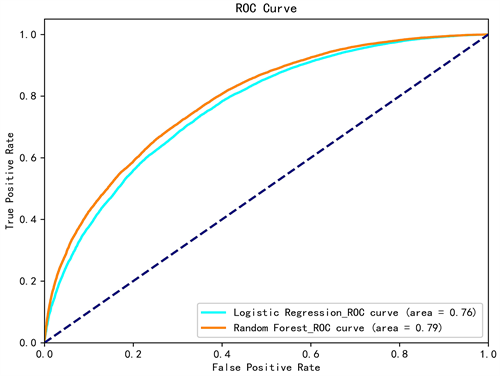
Figure 3. Comparison between random forest and logistic regression model ROC curve
图3. 随机森林与逻辑回归模型 ROC曲线对比图
(1) 随机森林模型的预测准确率为0.75,逻辑回归模型的预测准确率为0.71,可见随机森林模型预测效果更好,优于逻辑回归模型。
(2) 从F1-measure值看,随机森林模型F1-measure值为0.72,逻辑回归模型F1-measure为0.70,可见随机森林模型进行预测时比起逻辑回归模型更加稳定。
(3) 从图3中可以得知随机森林模型AUC的值比逻辑回归模型的值要高一些,随机森林模型分类效果要比逻辑回归模型表现更好。
4. 总结
(1) 本文构建的两个交通事故严重程度预测模型都能够预测交通事故的严重程度,其次交通事故数据具有很多的维度,随机森林算法对于多维数据有很好的适应能力,并且能够获得较好的预测效果。
(2) 通过对交通事故的严重程度进行预测,在研究的过程中知道是否超速,天气状况、事故发生的时间和地点、光照条件等因素都与交通事故严重程度有较大的关系。因此在交通事故严重程度进行预防或降低交通事故严重程度时都有很好的借鉴作用,在建设交通道路时可以尽量考虑这些因素,规划到设计之中,从而能够降低对交通事故造成的影响。
(3) 本文只使用了随机森林与逻辑回归两种建模算法,后续可以研究其它算法来进行验证,以期能够得到更好的预测效果。
基金项目
云南省科技创新团队计划项目“数据驱动的软件工程省科技创新团队”(2017HC012)。
文章引用
郭小刚,李 彤. 基于随机森林与逻辑回归模型的交通事故严重程度的预测研究
Prediction of Traffic Accident Severity Based on Random Forest and Logistic Regression Model[J]. 计算机科学与应用, 2019, 09(10): 1920-1927. https://doi.org/10.12677/CSA.2019.910215
参考文献
- 1. Ahmed, M.M. and Abdel-Aty, M.A. (2012) The Viability of Using Automatic Vehicle Identification Data for Real-Time Crash Prediction. IEEE Transactions on Intelligent Transportation Systems, 13, 459-468. https://doi.org/10.1109/TITS.2011.2171052
- 2. Shinohara, K., Okazaki, J., Sakuma, H., et al. (2003) A Clinical Survey of Motor Vehicle Crashes: What Most Influences the Severity of Patient’s Injuries? JSAE Review, 24, 357-358. https://doi.org/10.1016/S0389-4304(03)00040-7
- 3. Olutayo, V.A. and Eludire, A.A. (2014) Traffic Accident Analysis Using Decision Trees and Neural Networks. International Journal of Information Technology and Computer Science, 6, 22-28. https://doi.org/10.5815/ijitcs.2014.02.03
- 4. 李庚凭. 基于有序Logit和多项Logit模型的高速公路交通事故严重程度预测[D]: [硕士学位论文]. 西安: 长安大学, 2018.
- 5. Breiman, L. (2001) Random For-ests. Machine Learning, 45, 5-32. https://doi.org/10.1023/A:1010933404324
- 6. Breiman, L. (1996) Bagging Predictors. Machine Learning, 24, 123-140. https://doi.org/10.1007/BF00058655
- 7. Menezes, F.S.D., Liska, G.R., Cirillo, M.A., et al. (2017) Data Classification with Binary Response through the Boosting Algorithm and Logistic Regression. Expert Systems with Applications, 69, 62-73. https://doi.org/10.1016/j.eswa.2016.08.014
- 8. Lu, T., Zhu, D., Yan, L., et al. (2015) The Traffic Accident Hotspot Prediction: Based on the Logistic Regression Method. International Conference on Transportation Information & Safety, Wuhan, 25-28 June 2015, 107-110. https://doi.org/10.1109/ICTIS.2015.7232194
- 9. 李卓冉. 逻辑回归方法原理与应用[J]. 中国战略新兴产业, 2017(28): 125-126.
