基于排队论模型的战时机场运行容量评估 Evaluation of Airdrome Operating Capacity in Wartime Based on Queuing Theory Model

doi:10.12677/CSA.2020.104073

Computer Science and Application
Vol. 10 No. 04 ( 2020 ), Article ID: 35210 , 8 pages
10.12677/CSA.2020.104073

Evaluation of Airdrome Operating Capacity in Wartime Based on Queuing Theory Model

Tianwei Ren, Di Shen, Fuping Yu, Xianghui Geng

●How to Cite this Article

Air Force Engineering University, Xi’an Shaanxi

Received: Apr. 1^st, 2020; accepted: Apr. 16^th, 2020; published: Apr. 23^rd, 2020

ABSTRACT

Military airdrome is an important support for the attack and defense of air force under the condition of joint operations. The size of its capacity can improve the intensity of military aircraft, reduce the time-base interval between continuous aircraft flows, and provide further reference for joint operations planning. This paper uses queuing model of wartime military aircraft take-off, landing and single runway theoretical calculation, the operational capacity is derived for the military airfield runway per unit time, can hold the largest aircraft operation, on the basis of theoretical research combined with example analysis, adjustment and supplement of wartime military airdrome to provide the reference suggestion.

Keywords:Military Airdrome, Operating Capacity, Queuing Model

基于排队论模型的战时机场运行容量评估

任天威，沈堤，余付平，耿祥辉

空军工程大学，陕西西安

收稿日期：2020年4月1日；录用日期：2020年4月16日；发布日期：2020年4月23日

摘要

军用机场是联合作战条件下空中力量攻防展开的重要依托，其容量的提升对提高军用航空器出动强度，减少连续飞机流之间的时间间隔具有重要的现实意义。本文运用排队系统模型，对战时军用航空器起飞、着陆和单跑道混合运行容量进行了理论计算，推导出战时军用机场跑道单位时间内所能容纳的最大运行飞机数量，在理论研究的基础上结合实例进行分析，为战时机场调整和补充军用飞机提供参考建议。

关键词 :军用机场，运行容量评估，排队论模型

This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).

http://creativecommons.org/licenses/by/4.0/

1. 引言

过去，无论是全军还是空军组织的各类演习演练活动，作战筹划过程中对于各类行动指定空域和机场的使用，所采取的基本都是定性分析办法，预估一个大概范围，使用方式非常粗放，空域和机场资源浪费严重。究其根本，主要还是缺少系统、完整的战场空域和机场的容量评估理论方法。可见，从作战实践的角度，加强战时空域和机场容量评估问题研究迫在眉睫。战时机场实际容量是在相应的可接受的延误程度下的单位时间内机场可处理的交通量，与平均延误时间密切相关，其大小是空中作战计划制定的重要依据。由于机场空侧一个组成部分的运行一般是相互独立的，因而整个机场空侧的容量为其组成部分中最受限制的容量——跑道容量所控制 [1]。战时机场运行环境错综复杂，涉及飞行器数量多，受到任务、天气、地形等限制因素影响比较大，想要建立完全理论化的模型比较困难，因此建立的模型往往是基于一些假设。我们假设战时军用机场保障对象的起飞、着陆服从某个理论分布，从该分布计算样本的方法对军用机场保障对象流进行仿真。大量研究表明，战时军用机场起飞、着陆保障对象具有泊松流的特点，军用机场起飞、着陆保障符合排队模型 [2]。

2. 战时机场运行容量计算

大量研究表明，机场保障对象具有：平稳性、无后效性和普通性的特点。以战时单跑道全起降机场为例，满足泊松流条件：在不重叠时间区间内各飞机的全起降事件是相互独立的；对于充分小的时间间隔内，有一架飞机到达跑道系统的概率与时刻无关，而约与时间间隔的长成正比；对于充分小的时间间隔内，有两架或两架以上飞机到达跑道系统的概率极小，以至于可以忽略 [3]。战时单跑道系统为飞机起降提供保障可符合系统容量有限(M/M/1/N)排队模型。

令：

N——系统的最大容量；

$λ$ ——单位时间内机场系统平均着陆进近或起飞离场的平均到达数，即飞机平均到达率；

$μ$ ——单位时间内机场跑道系统平均能保障的全起降飞机数，即机场平均保障率；

t——机场跑道的平均全起降保障时间，与 $μ$ 互为倒数，即单位时间内机场跑道所保障的飞机起降均值数。

根据排队理论，则有：

机场跑道的起降保障强度

$ρ = λ t$ (1)

跑道系统空闲状态的概率

$p_{0} = \frac{1 - ρ}{1 - ρ^{N + 1}}, ρ \neq 1$ (2)

跑道系统中飞机数为n的概率

$P_{n} = \frac{1 - ρ}{1 - ρ^{N + 1}} ρ^{n}, n \leq N$ (3)

跑道系统中飞机的队长

$L_{s} = \frac{ρ}{1 - ρ} - \frac{(N + 1) ρ^{(N + 1)}}{1 - ρ^{(N + 1)}}, ρ \neq 1$ (4)

跑道系统队列中飞机的等待时间

$W_{s} = \frac{L_{s}}{μ (1 - P_{0})}$ (5)

下面分别从战时机场的全起、降以及混合运行模式来说明战时机场的运行容量。

3. 战时机场全起飞运行容量计算

由于我军作战飞机性能限制，其起飞容量也有限制。根据排队理论，机场起飞保障符合顾客源为有限(M/M/1)模型。对单跑道的全起飞机场系统而言，对应的各式为:

机场跑道的起飞保障强度

$ρ_{d} = λ_{d} t_{d}$ (6)

起飞时跑道空闲状态的概率

$p_{0}_{d} = \frac{1 - ρ_{d}}{1 - ρ_{d}^{N + 1}}, ρ_{d} \neq 1$ (7)

起飞时跑道系统中飞机数为n的概率

$P_{n}_{d} = \frac{1 - ρ_{d}}{1 - ρ_{d}^{N_{d} + 1}} ρ_{d}^{n}, n \leq N_{d}$ (8)

飞机起飞队长

$L_{s d} = \frac{ρ_{d}}{1 - ρ_{d}} - \frac{(N_{d} + 1) ρ_{d}^{(N_{d} + 1)}}{1 - ρ_{d}^{(N_{d} + 1)}}, ρ_{d} \neq 1$ (9)

每架飞机起飞间隔时间

$W_{s}_{d} = \frac{L_{s d}}{μ_{d} (1 - P_{0 d})}$ (10)

式中

$t_{d}$ ——跑道平均起飞保障占用时间。

$λ_{d}$ ——飞机平均起飞率。

$μ_{d}$ ——跑道平均起飞保障率。

现假设飞机全起飞模式时最大运行容量为 $N_{d}$ ，每架飞机起飞放行等待时间为 $W_{q}_{d}$ ，在起飞队列中等待的最大时间为 $t_{d}_{\max}$ ，要求 $W_{q}_{d} \leq t_{d \max}$ ，即

$W_{q}_{d} = W_{s}_{d} - t_{d} = \frac{\frac{ρ_{d}}{1 - ρ_{d}} - \frac{(N_{d} + 1) ρ_{d}^{(N_{d} + 1)}}{1 - ρ_{d}^{(N_{d} + 1)}} - (1 - \frac{1 - ρ_{d}}{1 - ρ_{d}^{(N_{d} + 1)}})}{λ_{d} (1 - \frac{1 - ρ_{d}}{1 - ρ_{d}^{(N_{d} + 1)}} ρ_{d}^{N_{d}})} \leq t_{d \max}$ (11)

化简得

$\frac{ρ_{d}^{(N_{d} + 1)} - ρ_{d}^{2}}{ρ_{d} - 1} + (\frac{t_{d \max}}{t_{d}} - N_{d}) ρ_{d}^{N_{d}} \leq \frac{t_{d \max}}{t_{d}}$ (12)

令 $f (N_{d}) = \frac{ρ_{d}^{(N_{d} + 1)} - ρ_{d}^{2}}{ρ_{d} - 1} + (\frac{t_{d \max}}{t_{d}} - N_{d}) ρ_{d}^{N_{d}} - \frac{t_{d \max}}{t_{d}}$ (13)

对函数 $f (N_{d})$ 求导，所得的极大值即为战时单跑道全起飞运行容量 $N_{d}$ ，解得

$N_{d} = \frac{t_{d \max}}{t_{d}} - \frac{1}{\ln ρ_{d}} - \frac{ρ_{d}}{1 - ρ_{d}}$ (14)

4. 战时机场全着陆运行容量计算

同理，据排队理论，机场着陆保障符合(M/M/1)模型。现假设飞机全着陆模式时最大运行容量为 $N_{a}$ 对单跑道的全着陆机场系统而言，对应的各式为：

机场跑道的着陆保障强度

$ρ_{a} = λ_{a} t_{a}$ (15)

着陆时跑道空闲状态的概率

$P_{0 a} = \frac{1 - ρ_{a}}{1 - ρ_{a}^{N_{a} + 1}}, ρ_{a} \neq 1$ (16)

着陆时跑道系统中飞机数为n的概率

$P_{n}_{a} = \frac{1 - ρ_{a}}{1 - ρ_{a}^{N_{a} + 1}} ρ_{a}^{n}, n \leq N_{a}$ (17)

飞机着陆队长

$L_{s a} = \frac{ρ_{a}}{1 - ρ_{a}} - \frac{(N_{a} + 1) ρ_{a}^{(N_{a} + 1)}}{1 - ρ_{a}^{(N_{a} + 1)}}, ρ_{a} \neq 1$ (18)

飞机着陆间隔时间

$W_{s}_{a} = \frac{L_{s a}}{μ_{a} (1 - P_{0}_{a})}$ (19)

飞机着陆放行等待时间

$W_{q}_{a} = W_{s a} - \frac{1}{μ_{a}} = \frac{\frac{ρ_{a}}{1 - ρ_{a}} - \frac{(N_{a} + 1) ρ_{a}^{(N_{a} + 1)}}{1 - ρ_{a}^{(N_{a} + 1)}} - (1 - \frac{1 - ρ_{a}}{1 - ρ_{a}^{(N_{a} + 1)}})}{λ_{a} (1 - \frac{1 - ρ_{a}}{1 - ρ_{a}^{(N_{a} + 1)}} ρ_{a}^{N_{a}})}$ (20)

式中：

$t_{a}$ ——机场跑道保障着陆平均占用时间。

$λ_{a}$ ——飞机平均着陆率。

$μ_{a}$ ——跑道平均着陆保障率。

设在着陆放行等待队列中等待的最大时间为 $t_{a \max}$ ，要求 $W_{q}_{a} \leq t_{a \max}$ ，即

$W_{q}_{a} = W_{s}_{a} - \frac{1}{μ_{a}} = \frac{\frac{ρ_{a}}{1 - ρ_{a}} - \frac{(N_{a} + 1) ρ_{a}^{(N_{a} + 1)}}{1 - ρ_{a}^{(N_{a} + 1)}} - (1 - \frac{1 - ρ_{a}}{1 - ρ_{a}^{(N_{a} + 1)}})}{λ_{a} (1 - \frac{1 - ρ_{a}}{1 - ρ_{a}^{(N_{a} + 1)}} ρ_{a}^{N_{a}})} \leq t_{a \max}$ (21)

化简得

$\frac{ρ_{a}^{(N_{a} + 1)} - ρ_{a}^{2}}{ρ_{a} - 1} + (\frac{t_{a \max}}{t_{a}} - N_{a}) ρ_{a}^{N_{a}} \leq \frac{t_{a \max}}{t_{a}}$ (22)

令 $f (N_{a}) = \frac{ρ_{a}^{(N_{a} + 1)} - ρ_{a}^{2}}{ρ_{a} - 1} + (\frac{t_{a \max}}{t_{a}} - N_{a}) ρ_{a}^{N_{a}} - \frac{t_{a \max}}{t_{a}}$ (23)

对函数 $f (N_{a})$ 求导，所得的极大值即为战时单跑道全着陆运行容量 $N_{a}$ ，解得

$N_{a} = \frac{t_{a \max}}{t_{a}} - \frac{1}{\ln ρ_{a}} - \frac{ρ_{a}}{1 - ρ_{a}}$ (24)

5. 战时机场混合起降运行容量计算

由于起飞飞机之间、着陆飞机之间、起飞飞机和着陆飞机之间的间隔都必须满足战时管制规定，因此起飞流和着陆流相互耦合，混合运行关系 [4]。对于混合起降，根据实际工作程序以及相关规定，一般情况下着陆飞机比起飞飞机对跑道有更高的优先权。在着陆飞机占绝对优先权的情况下，可以认为着陆飞机的运行不受起飞飞机的影响 [5]。故在混合起降运行时着陆飞机的延误和容量可以用上式计算；但是起飞受着陆飞机影响，对于起飞的飞机只有在着陆飞机之间有足够的空隙时才能插缝放行 [6]。如图1所示：

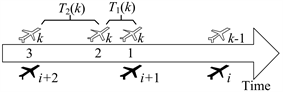注：1) 轴上方为起飞航空器，轴下方为着陆航空器；2) 1、2、3代表起飞航空器3种插缝放行情形在时间轴上的位置。

Figure 1. Schematic diagram of slotting release

图1. 插缝放行情形示意图

情形1表示第i架与第i + 1架着陆飞机间隔能够满足第k − 1架与第k架飞机起飞间隔要求时，第k架飞机于第i + 1架飞机着陆后立即起飞。此时第k架距第i + 1架飞机着陆后的等待时间 $T_{i} (k) = 0$ 。

情形2表示第i架与第i + 1架着陆飞机间隔不能够满足第k − 1架与第k架飞机起飞间隔要求时，第k架飞机需于第i + 1架飞机着陆后等待，直到满足第k − 1架与第k架飞机起飞间隔要求。此时等待时间为 $T_{1} (k)$ 。

情形3表示情形2中第k架飞机等待时间 $T_{1} (k)$ 后，第i + 2架飞机距第k架飞机间隔，不满足起降飞机规定间隔要求，此时航空器还需等待 $T_{2} (k)$ 。

在这三种情况下，设混合起降飞机平均起飞放行等待时间为 $W_{d}$ ，平均起飞间隔为 ${W^{'}}_{q d}$ ，平均等待间隔为 $W_{T (k)}$

${\begin{cases} W_{d} = {W^{'}}_{q d} + W_{T (k)} \\ {W^{'}}_{q d} = \frac{λ_{d} {t^{'}}_{d}^{2}}{1 - λ_{d} {t^{'}}_{d}} \\ W_{T (k)} = \frac{g_{a} {t^{'}}_{a}^{2}}{1 - λ_{a} {t^{'}}_{a}} \end{cases}$ (25)

式中： ${t^{'}}_{d}$ 表示相继起飞的飞机平均间隔时间； ${t^{'}}_{a}$ 表示不能放行的起飞飞机平均等待间隔时间； $g_{a}$ 表示两架相继到达飞机之间发生空档平均率， $g_{a} = P {\frac{1}{λ_{a}} > {t^{'}}_{a}}$ ，则当混合起降飞机平均起飞放行等待时间 $W_{d}$ 最小时，起飞容量达到最大 [7]。

对 $W_{d} = {W^{'}}_{q d} + W_{T (k)} = \frac{λ_{d} {t^{'}}_{d}^{2}}{1 - λ_{d} {t^{'}}_{d}} + \frac{g_{a} {t^{'}}_{a}^{2}}{1 - λ_{a} {t^{'}}_{a}}$ 求导取极小值时，得

$λ_{d} = \frac{W_{d}}{2 {t^{'}}_{d} W_{d} + 2 {t^{'}}_{d}^{2}} + \frac{W_{d} + {t^{'}}_{d} - g_{a} \cdot t_{a}^{2}}{8 {t^{'}}_{d} t_{a}^{2} (W_{d} + {t^{'}}_{d})}$ (26)

由上可知，战时混合起降中机场跑道满负荷运行时，该机场跑道的起飞极限容量 ${N^{'}}_{d}$ 为

${N^{'}}_{d} = λ_{d}$ (27)

战时混合起降中机场跑道满负荷运行时，该机场跑道的容量N为

$N = {N^{'}}_{d} + N_{a}$ (28)

6. 实例分析

本节以某机场保障某次演习任务为例，进行跑道容量分析。

在执行演习任务中测量得到相关演习飞行中飞机起降观测数据以及飞行起降平均占用跑道时间数据如表1和表2所示：

Table 1. Aircraft takeoff and landing observation data in the exercise flight

表1. 演习飞行中飞机起降观测数据

Table 2. Data of average runway time occupied by takeoff and landing

表2. 飞行起降平均占用跑道时间数据

对表1中数据进行统计计算得：平均起飞间隔时间间隔 $τ_{d} = 11.1$ min/批次；平均返场着陆间隔时间间隔 $τ_{a} = 8.9$ min/批次，根据实际情况，为求得飞机连续起飞时机场跑道的极限容量，选取 ${t^{'}}_{a} = 3 \min$ ，即允许连续放飞飞机的最小时间间隔为3 min，参考表1可以得出双机编队时相随出发的飞机平均最小时间间隔 ${t^{'}}_{d} = 5 \min$ 。

1) 计算跑道起飞容量。

假设飞机起飞放行最大等待时间 $t_{d \max} = 30 \min$ ，对表1、表2中数据进行统计计算得：平均起飞间隔时间间隔 $τ_{d} = 11.1$ min/批次，平均跑道保障起飞时间 ${τ^{'}}_{d} = 65.75$ ，代入式

$N_{d} = \frac{t_{d \max}}{t_{d}} - \frac{1}{\ln ρ_{d}} - \frac{ρ_{d}}{1 - ρ_{d}}$

计算该机场跑道的起飞极限容量为 $N_{d} = 22.2$ 。取整数得空中排队的最大着陆容量为 $N_{d} = 22$ 架次/h。

2) 计算跑道着陆容量。

假设飞机空中最大等待时间 $t_{\max} = 30 \min$ ，对表1、表2中数据进行统计计算得:平均返场着陆间隔时间间隔 $τ_{a} = 8.9$ min/批次，平均跑道保障着陆时间 ${τ^{'}}_{a} = 93.58$ ，代入式

$N_{a} = \frac{t_{a \max}}{t_{a}} - \frac{1}{\ln ρ_{a}} - \frac{ρ_{a}}{1 - ρ_{a}}$

计算该机场跑道的着陆极限容量为 $N_{a} = 18.8$ 。取整数得空中排队的最大着陆容量为 $N_{a} = 18$ 架次/h。

3) 计算跑道混合起降容量。

根据实际情况，为求得飞机混合起降时机场跑道的极限容量，选取允许连续放飞飞机的最小时间间隔 ${t^{'}}_{a} = 3 \min$ ，参考表1可以得出两架相随出发的飞机平均最小时间间隔 ${t^{'}}_{d} = 5.1 \min$

${\begin{cases} g_{a} = P {\frac{1}{λ_{a}} > {t^{'}}_{a}} \\ W_{d} = {W^{'}}_{q d} + W_{T (k)} = \frac{λ_{d} {t^{'}}_{d}^{2}}{1 - λ_{d} {t^{'}}_{d}} + \frac{g_{a} {t^{'}}_{a}^{2}}{1 - λ_{a} {t^{'}}_{a}} \\ λ_{d} = \frac{W_{d}}{2 {t^{'}}_{d} W_{d} + 2 {t^{'}}_{d}^{2}} + \frac{W_{d} + {t^{'}}_{d} - g_{a} \cdot t_{a}^{2}}{8 {t^{'}}_{d} t_{a}^{2} (W_{d} + {t^{'}}_{d})} \end{cases}$

代入计算得 $g = \sum_{0}^{1} \frac{2}{λ_{a}} \cdot {t^{'}}_{a}^{2} \cdot e^{- λ_{a} {t^{'}}_{a}} = 0.747$ ， $ω_{d} \to {\bar{τ}}_{d} = 11.1 \min$ ， $λ_{d} = 9.13$ ，取整数得 ${N^{'}}_{d} = λ_{d} = 10$ 。

4) 设跑道运行容量为N，则

$N = \max {{N^{'}}_{d} + N_{a}, N_{a}, N_{d}}$

跑道的运行容量为28架次/h。

7. 结束语

机场容量是决定飞机可出动架次的关键因素，对飞机空中飞行时间产生了重要影响 [8]。本文运用排队论模型，基于数学计算模型的评估方法，计算出作战飞机起飞和着陆对机场容量的需求，其优点是简单、快速、投入少，评估结果较为准确；缺点是没有量化考虑人为因素，此外只对军用单跑道机场进行了运行容量评估，建立的模型不能很好地与军用双跑道机场对应。机场容量问题是一项非常复杂的系统工程问题，由于研究条件和时间的限制，本文不可能做到全面研究与实现。战时机场运行容量模型的建立对战时作战筹划，以及指挥决策人员对作战飞机调配和补充有一定的参考作用。对于战场空域容量评估问题的理解，我们不但要在民航容量评估理论的基础上进行重新剪裁与嫁接，还必须有创新，因此理论研究价值与意义非常明显。

文章引用

任天威,沈堤,余付平,耿祥辉. 基于排队论模型的战时机场运行容量评估
Evaluation of Airdrome Operating Capacity in Wartime Based on Queuing Theory Model[J]. 计算机科学与应用, 2020, 10(04): 702-709. https://doi.org/10.12677/CSA.2020.104073

参考文献

1. 孔航, 胡明华, 姚逸, 裔田园. 不同运行模式下跑道容量评估技术研究[J]. 航空计算技术, 2017.

2. 唐应辉, 唐小我. 排队论-基础与分析技术[M]. 北京: 科学出版社, 2006.

3. Graham, R. (2015) RECAT-EU European Wake Turbulence Categorisation and Separation Minima on Approach and Departure. Eurocontrol, Europe.

4. Federal Aviation Administration (2013) SAFO 12007. Re-Categorization (RECAT) of FAA Wake Turbulence Separation Categories at Specific Airports. Federal Aviation Administration, Washington, DC.

5. 王声. 战时机场保障概论[M]. 北京: 空军后勤部机场管理部, 2005.

6. 王莉莉, 陈云翔. 考虑机场容量的作战飞机调配保障模型[J]. 电光与控制, 2010, 01-0054-03.

7. 潘卫军, 冉斌, 吴郑源, 朱新平 . 尾流间隔分类标准综述[J]. 中国民航飞行学院学报, 2019(2): 54-57.

8. 王声. 战时机场保障概论[M]. 北京: 空军后勤部机场管理部, 2005.

期刊菜单