Advances in Applied Mathematics
Vol.05 No.04(2016), Article ID:19034,10
pages
10.12677/AAM.2016.54078
Modified Moving Least Square Method
Xi Zhang, Renzhong Feng
School of Mathematics and System Science, Beijing University of Aeronautics and Astronautics, Beijing

Received: Nov. 2nd, 2016; accepted: Nov. 19th, 2016; published: Nov. 24th, 2016
Copyright © 2016 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
In this paper, based on the MLH (Least-Hardy Moving) method, we present a modified MLS (Moving Least-Squares) method by introducing the correction weight in MLS method. The method is the same as the MLH method, which can effectively approximate the scattered data with outliers. At the same time, this method avoids the problem of MLS method to approximate this kind of scattered data, and its computing efficiency is significantly better than that of MLH method. In order to improve the accuracy of approximation, we also introduce the natural neighbor points, which replace the role of MLS weight function.
Keywords:Scattered Data, Outlier, Moving Least Square (MLS), Moving Least-Hardy Approximation (MLH), Modified Moving Least Square (MMLS)

修正的移动最小二乘方法
张熙,冯仁忠
北京航空航天大学,数学与系统科学学院,北京

收稿日期:2016年11月2日;录用日期:2016年11月19日;发布日期:2016年11月24日

摘 要
本文在MLH (Moving Least-Hardy)逼近方法的基础上,通过在MLS (Moving Least-Squares)方法中引入修正权给出了一种修正的MLS方法。该方法与MLH方法一样,能够对带有奇异值的散乱数据进行有效的逼近,避免了MLS方法对这类数据逼近的不理想问题,并且其计算效率明显高于MLS方法。为了提高逼近值精度,该方法还引入了自然邻点,以自然邻点替代目标函数中权函数的作用。
关键词 :散乱数据,奇异值,移动最小二乘(MLS),移动最小Hardy逼近(MLH),修正移动最小二乘(MMLS)

1. 引言
散乱数据的函数逼近是函数逼近论中的一个重要问题,可以用于数据拟合、几何建模、CAD、医学成像、微分方程数值解等许多领域。构造逼近函数的常用方法有插值和拟合两类方法。McLain [1] 在1974年提出了一种移动最小二乘逼近方法(Moving Least-Squares简记为MLS)。这种方法可以用于任意维的散乱数据逼近且已用于计算机图形学、微分方程数值解等领域,见文献 [2] [3] [4] 。Zuppa,Armentano等在 [5] [6] 给出了MLS方法关于函数值、一阶和二阶导函数值的逼近误差分析。MLS方法在含有噪音数据的情况下,其逼近能力也有一定的保证。但是对于存在奇异值(采样值远远偏离真实值)的散乱数据,MLS方法的逼近效果就变得非常不理想,见 [7] 。针对采样数据中存在奇异值的情况,Levin [7] 在MLS的方法基础上提出了一种叫MLH (Moving Least-Hardy)的逼近方法。该方法对带奇异值的散乱数据逼近有着理想的逼近效果。
MLH方法是引进了Hardy’s multiquadric函数 [8] 并结合了MLS和 (移动最小
(移动最小 逼近)两种逼近方法的思想。当数据中存在奇异值时,MLH方法中发挥主要作用的是
逼近)两种逼近方法的思想。当数据中存在奇异值时,MLH方法中发挥主要作用的是 部分,而
部分,而 具有对奇异值不敏感性。与MLS不同的是MLH方法不是仅通过求解一次法方程就能获得解而是经过有限次迭代后的一个近似解,属于一种效率低的逼近方法。在本文中我们提出了一种修正的MLS (Moving Least-Squares)方法,它不仅具有MLH方法处理带奇异值散乱数据的能力,而且计算效率显著高于MLH。本文余下部分安排如下:第二节简要介绍MLH方法的工作原理;第三节介绍修正的MLS方法的构造;第四节为数值实验;第五节提出结论。
具有对奇异值不敏感性。与MLS不同的是MLH方法不是仅通过求解一次法方程就能获得解而是经过有限次迭代后的一个近似解,属于一种效率低的逼近方法。在本文中我们提出了一种修正的MLS (Moving Least-Squares)方法,它不仅具有MLH方法处理带奇异值散乱数据的能力,而且计算效率显著高于MLH。本文余下部分安排如下:第二节简要介绍MLH方法的工作原理;第三节介绍修正的MLS方法的构造;第四节为数值实验;第五节提出结论。
2. MLH方法概述
给定一组散乱数据 ,
, 其中的某些
其中的某些 的采样存在奇异值
的采样存在奇异值 ,即
,即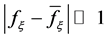 。MLH方法构造逼近这类散乱数据的方法如下:设
。MLH方法构造逼近这类散乱数据的方法如下:设 是一组基(
是一组基( 表示所有次数不超过
表示所有次数不超过 次的
次的 元多项式空间),取误差函数
元多项式空间),取误差函数
 (2.1)
(2.1)
其中 ,
,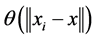 是权函数,
是权函数,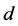 是一个小参数。
是一个小参数。 称为multiquadric函数,对于很小的
称为multiquadric函数,对于很小的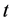 ,
,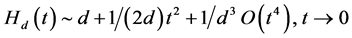 ;对于很大的
;对于很大的 ,
, 。
。
MLH方法是要确定一组值(解) 使误差函数(2.1)极小化,不难知道这组解是满足下列方程组
使误差函数(2.1)极小化,不难知道这组解是满足下列方程组
 . (2.2)
. (2.2)
奇异值点误差 ,该项变为
,该项变为 ,是关于
,是关于 的常数项,从而对奇异值不敏感。
的常数项,从而对奇异值不敏感。
因方程组(2.2)是一个关于 的非线性方程组,所以MLH方法定义了一个迭代过程来求解。它以
的非线性方程组,所以MLH方法定义了一个迭代过程来求解。它以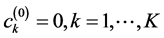 为初始值,通过下列迭代过程由第s步的值得到第s + 1步的值
为初始值,通过下列迭代过程由第s步的值得到第s + 1步的值
 (2.3)
(2.3)
记 ,上面的迭代过程可以写为
,上面的迭代过程可以写为
 , (2.4)
, (2.4)
其中(2.4)右端的矩阵 和向量
和向量 具体形式为
具体形式为
 (2.5)
(2.5)
对于迭代格式(2.4),文献 [7] 给出了以下两点结论:
1) 该方法经有限次迭代收敛;
2) 对带有奇异值的散乱数据具有较好的逼近性。
MLH方法具体描述详见 [7] 。该方法虽经有限次迭代达到收敛,但是每次迭代相当于求解一次移动最
小二乘问题,就是需要计算(2.4)中 ,导致其计算效率低下。我们针对这个问题提出了一
,导致其计算效率低下。我们针对这个问题提出了一
种修正的MLS方法(简记为MMLS方法),它只需求一次移动最小二乘问题,但对带有奇异值的散乱数据也有类似MLH一样的逼近性质。
3. 修正的MLS方法(MMLS)
MLS的目标是欲在 中找到一个多项式
中找到一个多项式 ,使下列误差达到极小:
,使下列误差达到极小:
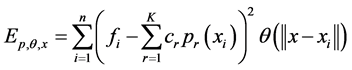 . (3.1)
. (3.1)
优化问题(3.1)的解向量 是下列法方程
是下列法方程
 ,(3.2)
,(3.2)
的解,其中 ,
,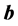 的表达式如下:
的表达式如下:
 ,
, . (3.3)
. (3.3)
如果从给定的散乱数据集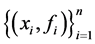 中去掉数据点
中去掉数据点 ,此时相应的MLS逼近问题的解是下列方程组的解
,此时相应的MLS逼近问题的解是下列方程组的解
 , (3.4)
, (3.4)
其中
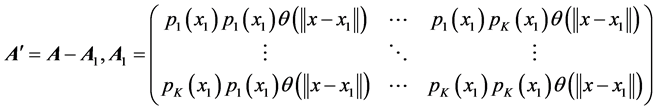 ,(3.5)
,(3.5)
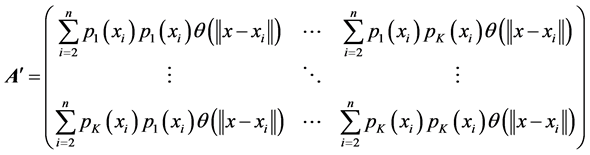 , (3.6)
, (3.6)
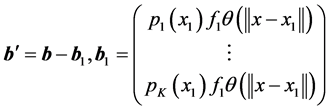 ,
, . (3.7)
. (3.7)
由(3.2)~(3.4)得
 。 (3.8)
。 (3.8)
把(3.5)和(3.7)代入(3.8)式的右端,展开得到
 . (3.9)
. (3.9)
文献 [2] [3] [4] [7] 给出:如果真实采样函数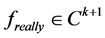 ,那么MLS的逼近误差
,那么MLS的逼近误差
 , (3.10)
, (3.10)
这里 通过MLS方法得到的逼近函数值,
通过MLS方法得到的逼近函数值, 是网格范数。那么通过(3.9)和(3.10)得到
是网格范数。那么通过(3.9)和(3.10)得到
 ,
, .
.
由于 是对称正定的,有
是对称正定的,有 。关于这个极限我们可以理解为当采样点取得非常密集时,去掉某一个散乱数据点对我们逼近的结果影响可以忽略。
。关于这个极限我们可以理解为当采样点取得非常密集时,去掉某一个散乱数据点对我们逼近的结果影响可以忽略。
假设在散乱点集 中,某些点处有
中,某些点处有 (
( 是真实的值,
是真实的值,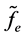 是采样得到的值)。不失一般性我们设
是采样得到的值)。不失一般性我们设 为奇异点(
为奇异点( )。那么,此时MLS的法方程是
)。那么,此时MLS的法方程是 ,其中
,其中
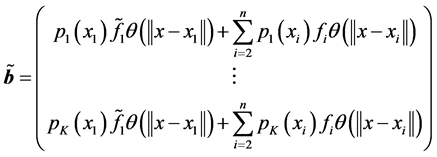 . (3.11)
. (3.11)
可以发现,奇异值的存在主要是将列向量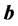 变成了
变成了 ,进而影响了解向量
,进而影响了解向量 。根据前述的记号
。根据前述的记号
 。 (3.12)
。 (3.12)
为了使得逼近多项式对应的权系数 ,
, 是任意正常数。根据线性方程组解的稳定性理论,如果
是任意正常数。根据线性方程组解的稳定性理论,如果 ,
, ,
, 是很小的正常数,那么
是很小的正常数,那么 可以满足
可以满足 ,这里
,这里 是无奇异值采样时最小二乘(3.2)的解。因此我们希望在带有奇异值的散乱数据的MLS逼近问题得到的法方程形式为
是无奇异值采样时最小二乘(3.2)的解。因此我们希望在带有奇异值的散乱数据的MLS逼近问题得到的法方程形式为
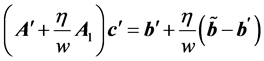 , (3.13)
, (3.13)
其中要求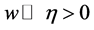 。这样,奇异值就被削弱成了一个较小的扰动项加在了不含奇异值的节点组法方程中。
。这样,奇异值就被削弱成了一个较小的扰动项加在了不含奇异值的节点组法方程中。
基于以上两种假设分析,我们可以构造一个修正的MLS方法来处理带奇异值的散乱数据逼近问题,其思想是:在我们修正的MLS方法中使用下列误差函数
 , (3.14)
, (3.14)
其中 ,
, 是标准MLS方法中的权函数,
是标准MLS方法中的权函数, 是对采样函数值
是对采样函数值 的一个修正表达式。加入这个修正就是为了针对存在奇异点值时,满足前述MLS逼近中去除奇异值点或者弱化奇异值点对逼近问题的影响。假设采样点
的一个修正表达式。加入这个修正就是为了针对存在奇异点值时,满足前述MLS逼近中去除奇异值点或者弱化奇异值点对逼近问题的影响。假设采样点 来自连续函数。
来自连续函数。
按照求解MLSS问题的方法对误差函数(3.14)极小化得到
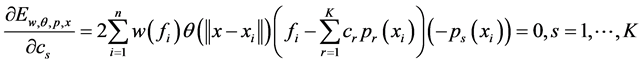 (3.15)
(3.15)
整合得到
 , (3.16)
, (3.16)
其中, 是法方程矩阵,
是法方程矩阵, 是一个列向量,它们的具体表达式如下:
是一个列向量,它们的具体表达式如下:

 .(3.17)
.(3.17)
关于修正的MLS问题(3.14)~(3.17)中的修正 ,我们希望其能根据数据
,我们希望其能根据数据 的不同情况满足相应的条件:
的不同情况满足相应的条件:
(i) 若数据中不存在奇异值时,我们希望当网格范数 时,
时, 满足
满足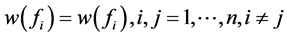 ,这样
,这样 退化成(3.3)中
退化成(3.3)中 ,MMLS逼近趋向于MLS逼近。
,MMLS逼近趋向于MLS逼近。
(ii) 若存在奇异值时,不妨假设存在一个奇异点 ,
, 是采样奇异值,
是采样奇异值, 是真实值,可以将
是真实值,可以将 转化为
转化为 ,其中
,其中
 ,
,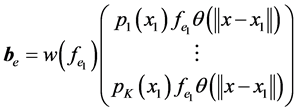 . (3.18)
. (3.18)
我们希望当网格范数 时,
时, 满足
满足 并且
并且 。当
。当 时,带有奇异点
时,带有奇异点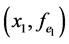 的逼近问题退化为关于散乱数据
的逼近问题退化为关于散乱数据 的MLS逼近问题,法方程形式变为(3.4);当
的MLS逼近问题,法方程形式变为(3.4);当 时,由于
时,由于 ,可以认为在法方程(3.4)的矩阵
,可以认为在法方程(3.4)的矩阵 加一个小的扰动矩阵
加一个小的扰动矩阵 ,向量
,向量 加一个小的扰动向量
加一个小的扰动向量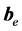 ,法方程形式变为(3.13)。因此,有
,法方程形式变为(3.13)。因此,有 ,对
,对 。
。
注释1:修正的MLS方法是考虑了关于目标点处的函数值信息对逼近效果的影响, 是关于采样值的修正,
是关于采样值的修正,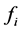 的值与真实值的偏离越大其对逼近的影响越小。
的值与真实值的偏离越大其对逼近的影响越小。
注释2:修正的MLS方法同样也可以逼近存在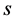 (
( )个奇异值的散乱数据。
)个奇异值的散乱数据。
根据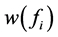 所需要满足的条件(i)和(ii),我们给出下列两个
所需要满足的条件(i)和(ii),我们给出下列两个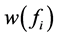 模型。
模型。
模型一:
 (其中是一个小参数)。
(其中是一个小参数)。
这个模型利用符号函数的性质排除奇异点。如果存在奇异值将退化为不含有奇异值的逼近问题(3.4)。且当 时,
时, 满足条件(i)、(ii)。
满足条件(i)、(ii)。
模型二:
 .
.
 是一个小参数,
是一个小参数, 。
。 可以看作
可以看作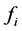 对
对 的方差贡献率的倒数,或者
的方差贡献率的倒数,或者 对集合
对集合 的偏离程度。偏离程度越高
的偏离程度。偏离程度越高 越小,反之越大。
越小,反之越大。 根据
根据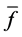 而定,
而定, 正比于
正比于 。因为我们的模型
。因为我们的模型 不能严格满足(i)、(ii)中的设定,在
不能严格满足(i)、(ii)中的设定,在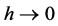 的条件下,
的条件下, 。但是模型的作用同前述分析。
。但是模型的作用同前述分析。
为了测试这两个模型的效果,我们在第四节的数值试验中进行了验证。
4. 数值实验
4.1. 自然邻点
MLS中非负权函数 一般被选取成当
一般被选取成当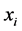 距离
距离 越大时,
越大时,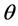 值快速下降接近零,甚至
值快速下降接近零,甚至 被选成具有紧支撑性,即
被选成具有紧支撑性,即 。所以移动最小二乘中权函数的作用是选取目标点
。所以移动最小二乘中权函数的作用是选取目标点 附近的
附近的
参与逼近的数据节点。自然邻点是“最靠近”目标点的邻域节点。在本节我们使用自然邻点来替代权函数的这种选取性质,即修正MLS逼近中通过使用自然邻点作为(3.14)中的逼近节点,而不是通过权函数来选取逼近节点集。这样做既提高了MMLS的计算效率同时又保证逼近精度。图1是二维平面上的自然邻点的一个示例。自然邻点的详细内容和选取方法见 [9] [10] 。
在目标函数(3.1)和(3.14)中,如果 ,根据MLS逼近理论知道逼近函数将会是一个插值于这
,根据MLS逼近理论知道逼近函数将会是一个插值于这 个散乱节点的插值多项式。因此,在使用自然邻点时,如果得到的自然邻点个数小于
个散乱节点的插值多项式。因此,在使用自然邻点时,如果得到的自然邻点个数小于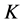 ,我们拟将自然邻点的自然邻点也加入其中。
,我们拟将自然邻点的自然邻点也加入其中。
图2给出了一组二维散乱节点,红色的点代表目标点的自然邻点,绿色的点代表红色点自然邻点,黑色点代表绿色点的自然邻点,我们称为三层自然邻点模板。在后面的数值试验中,将统一采用这种三层自然邻点模板进行逼近。
4.2. MMLS方法与MLH方法的逼近精度比较
我们选取Franke函数作为被采样函数,其表达式为

选择(2.1)和(3.14)中 ,目标逼近散乱点取511个,如图3中红色点表示,为了消除边界影响加入蓝色散乱点,这样散乱点总个数为1000个。我们加入的奇异点为
,目标逼近散乱点取511个,如图3中红色点表示,为了消除边界影响加入蓝色散乱点,这样散乱点总个数为1000个。我们加入的奇异点为 ,其中真实值为
,其中真实值为 ,
, 。模型中
。模型中 。
。
本文使用下列两种误差表达式
 ,
,
fi表示精确函数值, 表示逼近的函数值
表示逼近的函数值
 ,
,

Figure 1. Target point x and its surrounding natural neighbor points 
图1. 目标点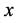 及其周围的自然邻点
及其周围的自然邻点
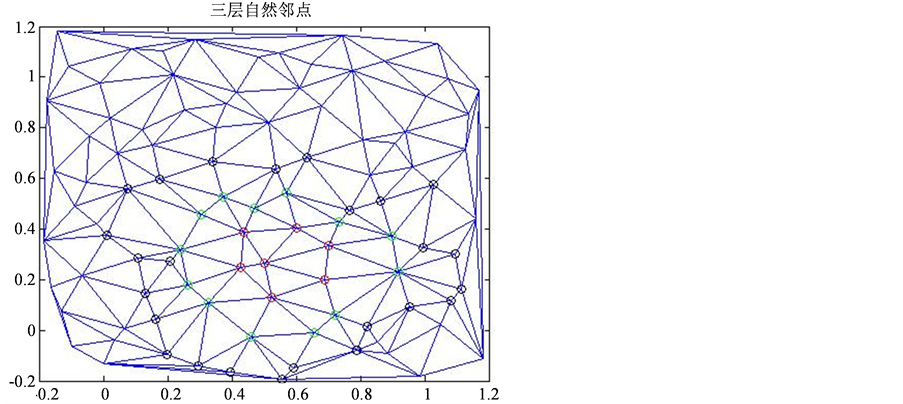
Figure 2. Extended three layer natural neighbor points
图2. 扩展的三层自然邻点

Figure 3. Two dimensional scattered nodes (red dots represent the point of approximation, the blue dots around the red dots are the scattered nodes to eliminate the influence of the boundary)
图3. 二维散乱节点(红色点代表待逼近点,围绕红色点的蓝色点是为了消除边界影响加入的散乱节点)
表1说明了,MMLS模型一是将含有奇异值的散乱节点逼近问题转化为排除散乱节点后的MLS逼近问题,MMLS模型二是将奇异值的影响转化为了求解过程中法方程和右端向量的小扰动的影响。在这里模型一优于模型二。
从表2看出MMLS模型二的精度稍低于MLH方法,但计算效率却优于MLH方法,这和MLH方法需要求解多遍移动最小二乘问题,而MMLS只需求解一次该问题的结论一致。
表3中的噪音是按照 ,如果是5%的噪音,s是[−5,5]之间的随机数。从表中的结果看出,在相同条件下,MLH方法的逼近效果稍优于MMLS方法,但是从计算效率看,MMLS方法明显优于MLH方法。这也说明了MMLS方法对含有奇异值和噪音的数据集逼近都能保证一定的精度,但是计算效率优于MLH方法。
,如果是5%的噪音,s是[−5,5]之间的随机数。从表中的结果看出,在相同条件下,MLH方法的逼近效果稍优于MMLS方法,但是从计算效率看,MMLS方法明显优于MLH方法。这也说明了MMLS方法对含有奇异值和噪音的数据集逼近都能保证一定的精度,但是计算效率优于MLH方法。
5. 结论
文中提出的MMLS方法同MLH方法一样,能够解决带有奇异点和小噪声的散乱数据集的逼近问题,但本文中的方法较MLH方法在计算效率上有着显著的提高。可是本文中的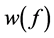 函数还可以进一步的改进和提高,因为针对带有奇异点的散乱数据集的逼近中,更加合理的选择函数
函数还可以进一步的改进和提高,因为针对带有奇异点的散乱数据集的逼近中,更加合理的选择函数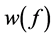 将会直接影响我们对于逼近问题的逼近精度。
将会直接影响我们对于逼近问题的逼近精度。
Table 1. Error comparison of MMLS method with two different correction methods
表1. 两种不同修正权的MMLS方法误差对比
Table 2. Error comparison between MMLS method and MLH method
表2. MMLS方法与MLH方法误差对比
Table 3. Scattered data approximation error comparison with outliers and noise
表3. 带有奇异值和噪音的散乱数据逼近对比
基金项目
该工作受到国家自然科学基金项目(No.11271041)的支持。
文章引用
张熙,冯仁忠. 修正的移动最小二乘方法
Modified Moving Least Square Method[J]. 应用数学进展, 2016, 05(04): 662-671. http://dx.doi.org/10.12677/AAM.2016.54078
参考文献 (References)
- 1. Mclain, D.H. (1974) Drawing Contours from Arbitrary Data Points. Computer Journal, 17, 318-324. https://doi.org/10.1093/comjnl/17.4.318
- 2. Fasshauer, G.E. and Zhang, J.G. (2007) Scattered Data Approximation of Noisy Data via Iterated Moving Least Squares.In: Lyche, T., Merrien, J.L. and Schumaker, L.L., Eds., Proceedings of Curve and Surface Fitting: Avignon 2006, Nashboro Press, 150-159.
- 3. Ding, H., Shu, C. and Tang, D.B. (2005) Error Estimates of Local Multiquadric-Based Differential Quadrature (LMQDQ) Method through Numerical Experiments. International Journal for Numerical Methods in Engineering, 63, 1513-1529. https://doi.org/10.1002/nme.1318
- 4. Wendland, H. (2004) Scattered Data Approximation. Cambridge University Press, Cambridge. https://doi.org/10.1017/CBO9780511617539
- 5. Zuppa, C. (2001) Error Estimates for Moving Least Square Approximations. Applied Numerical Mathematics, 37, 397-416. https://doi.org/10.1016/S0168-9274(00)00054-4
- 6. Armentano, M.G. (2001) Error Estimates in Sobolev Spaces for Moving Least Square Approximations. Society for Industrial & Applied Mathematics, 39, 38-51. https://doi.org/10.1137/s0036142999361608
- 7. Levin, D. (2014) Between Moving Least-Squares and Moving Least-l1. BIT Numerical Mathematics, 55, 781-796. https://doi.org/10.1007/s10543-014-0522-0
- 8. Hardy, R.L. (1971) Multiquadric Equations of Topography and Other Irregular Surfaces. Journal of Geophysical Research Atmospheres, 76, 1905-1915. https://doi.org/10.1029/JB076i008p01905
- 9. Sibson, R. (1981) A Brief Description of Natural Neighbour Interpolation. Interpreting Multivariate Data, 21, 21-36.
- 10. Watson, D.F. (1985) Natural Neighbour Sorting. Australian Computer Journal, 17, 189-193.
