Advances in Applied Mathematics
Vol.06 No.07(2017), Article ID:22554,12
pages
10.12677/AAM.2017.67109
On the Number of D-Points on a Line in the Tiling (3.6.3.6)
Lin Peng, Liping Yuan
College of Mathematics and Information Science, Hebei Normal University, Shijiazhuang Hebei
Received: Oct. 8th, 2017; accepted: Oct. 24th, 2017; published: Oct. 31st, 2017

ABSTRACT
A vertex of the Archimedean tiling (3.6.3.6) is called a D-point. In this paper, we first investigate the number of D-points lying on any given line in the plane, and prove that all the lines can be classified into three categories according to the numbers of D-points lying on them, namely, no D-point, one and only one D-point and an infinitely many D-points. We also give the whole characterizations of those three types of lines by some necessary and sufficient conditions. Furthermore, we consider the broadest paths that contain no D-points in their interiors in any given direction
.
Keywords:Archimedean Tiling, Lattice, Line, D-Point, Broadest Path
铺砌(3.6.3.6)中直线上的D-点数
彭琳,苑立平
河北师范大学数学与信息科学学院,河北 石家庄
收稿日期:2017年10月8日;录用日期:2017年10月24日;发布日期:2017年10月31日

摘 要
阿基米德铺砌(3.6.3.6)的顶点称为D-点。论文首先研究了平面内任意给定直线上的D-点数,证明了所有直线按其所含D-点数可分为三类,即不含D-点、含且仅含一个D-点与含无穷多个D-点,同时给出了刻画这三类直线的充要条件,进而探讨了
方向上内部不含D-点的最宽路径问题。
关键词 :阿基米德铺砌,格,直线,D-点,最宽路径

Copyright © 2017 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
平面铺砌
是指由可数个闭集构成的集族
,满足
与
。每个闭集
称为铺砌
的铺砌元。一个平面铺砌
中有限个(至少两个)铺砌元的交或为空集,或为孤立点,或为一段弧,称孤立点为铺砌顶点,弧为铺砌边。
若铺砌
的每个铺砌元均为多边形且每个铺砌元的顶点和边恰好是整个铺砌的顶点和边,则称
为边对边铺砌 [1] 。平面铺砌中与某一个铺砌顶点关联的所有铺砌元的个数、类型及彼此的邻接顺序,统称为该铺砌顶点的顶点特征。若平面铺砌
是以正多边形为铺砌元、各顶点的顶点特征均相同的边对边铺砌,则称
为阿基米德铺砌 [1] 。阿基米德铺砌有且仅有11种,如图1所示。
设u,v为二维平面内两个线性无关的向量,称点集
为由向量u与向量v生成的一般格
,一般格
中的点称为格点。特别地,若u与v是两个单位正交向量,则称
为整数格。显然,铺砌元的边长为1的阿基米德铺砌(44)的顶点集即为整数格。因此,将数的几何中关于格点的研究方法和相关理论推广到阿基米德铺砌中是一个有意义的研究课题。
在文献 [2] 中,Olds等人首先讨论了平面内任意给定直线上所含整数格点的个数问题,指出所有直线按其所含整数格点的个数可以分为三类,即不含任何整数格点、含且仅含一个整数格点与含无穷多个整数格点。文献 [3] 中创造性地将此结果推广到了一般格与铺砌(36)中,文献 [4] 中将相应的结果推广到了铺砌(33.42)中。
阿基米德铺砌(3.6.3.6)与一般格的联系十分紧密,本文将一般格中直线上的顶点计数的相关理论和方法推广到铺砌(3.6.3.6)中,按照所含D-点数对直线进行分类,同时给出刻画各类直线的充要条件;并进一步利用此结果讨论了内部无D-点的最宽路径问题。
2. 预备知识
阿基米德铺砌(3.6.3.6) (下记为
)由正六边形与正三角形铺砌元构成,为讨论方便,设其铺砌边的长为1。设D为铺砌
的顶点集,C为由铺砌
的所有正六边形铺砌元的中心构成的集合,并称D中的点为D-点,C中的点为C-点。D不具有一般格结构,但其可划分为3个一般格的不交并。不失一般性,以任一铺砌顶点为原点O,以过O及与O关联的正六边形的中心的直线为x-轴,建立如图2所示的坐标系。
设
为由向量
与向量
生成的一般格,则有
由
分别沿向量
和
平移得到
图1. 阿基米德铺砌
图2. 坐标系
显然有
。由
平移向量
可得到C,故有
进而根据顶点坐标的特征化简整理可得
铺砌元的边长为1的铺砌(36)的顶点集即为特殊的一般格,亦称为三角格T,称T中的点为T-点。而三角格T可由向量(1,0)与向量
生成,即
进一步化简可得
因此
。我们称集合
中的点为
-点,用符号
与
分别表示任意给定直线
上的
-点数与C-点数。
引理2.1:若点
,则
,其中
。
证明:已知点
,不妨设
,其中
,则
,显然有
且
,因此
。
引理2.2:设α为奇数,β为偶数,则有
(a) 若点
,则
。
(b) 若点
,则
。
(c) 若点
,则
。
证明:设点
,则可设
,其中
。不妨设
。
因为α为奇数,故可设
,则
,从而由
可得
,且易得
,因此
。
因为β为偶数,故可设
,则
,从而由
可得
,且易得
,因此
。
对于
或
,同理可证结论成立。
引理2.3:若点
,则点
;若点
,则点
。
证明:对点
综合应用引理2.1与引理2.2立即得证。
引理2.4:设点
,则有
(a) 若
,则
-点
-点
,C-点
C-点。
(b) 若
,则
-点
-点,
-点
-点,
-点
C-点,C-点
-点。
(c) 若
,则
-点
-点,
-点
-点,
-点
C-点,C-点
-点。
(d) 若
,则
-点
C-点,C-点
-点,
-点
-点,
-点
-点。
(e) 若点
,则点
。
其中,
表示P沿向量OQ平移后变为
,即
。
证明:任取三角格T中的点
,
,不妨设其相应坐标为
,其中
且满足
,
;
,
;
,
;
,
。令点
。
(a) 若
,则
,
。于是
,
,故点
与点
属于同一类型。因此,平移OQ后,
-点变为
-点,C-点变为C-点。
(b) 若
,则
,
。由于
,
,则点
;由于
,
,则点
;由于
,
,则点
;由于
,
,则点
。故平移OQ后,
-点变为
-点,
-点变为
-点,
-点变为C-点,C-点变为
-点。
情形(c),(d)类似于(b)可证。
(e) 记点
,则点
。根据引理2.3,由点
可得点
,于是综合(a)~(d)可得,若点
,则
,即点
,与条件点
矛盾,故
。
3. 平面内任意直线上的D-点数及其分布
设
为平面内任意一条直线,若直线l的斜率k不存在,可设其方程为
,则显然有下述定理:
定理3.1:设直线
,则
(a)
当且仅当
,其中
。
(b)
当且仅当
,其中
。
注意到,对于直线
,当m为奇数时,l上含无穷多个
-点与
-点,
-点与
-点交替出现且距离为
;当m为偶数时,l上仅含
-点且相邻两个
-点的距离为
。
现在我们考虑斜率存在的直线,不失一般性,可设直线l的方程为
。下面首先考虑
即l的方程为
的情形。
定理3.2:设直线
,则
当且仅当直线l上至少含有一个非原点的T-点。
证明:必要性显然成立。下证充分性:设直线l上含有非原点的T-点P,令点
,其中λ为偶数,显然有点
,进而综合引理2.1与引理2.2可得点
。因此
,即
。
推论3.3:设直线
,若
,则
。
证明:由定理3.2及其充分性的证明立即可得。
定理3.4:设直线
,则
的充要条件是
。
证明:必要性:已知
,则直线l上至少含有一个非原点的T-点P,不妨设
,其中
,
。根据条件可知直线l的斜率k存在,则
,于是
,故
。
充分性:已知
,则可设
,其中
,
。于是直线l的方程为
。令点
,易知点
且
,又由
且
可得点
,进而由定理3.2可得
。
定理3.5:设直线
,则
的充要条件是
。
证明:通过定理3.2分析可得,对于直线
而言,要么含无穷多个D-点,要么只含一个D-点即
,进而根据定理3.4立即可得定理3.5成立。
直线
可由直线
平移得到,接下来考虑直线
上的D-点数。
定义3.6:称直线
具有性质
,若存在
满足
,
或
,
,使得
。
引理3.7:设直线
,则
的充要条件为直线l具有性质
。
证明:必要性:由于
,可设l上含有D-点
,其中
,
,
或
,
,将其坐标代入直线方程
可得
。因此直线l具有性质
。
充分性:设直线l具有性质
,则可设
,其中
,
,
或
,
,从而直线l的方程为
。显然,点
,当
,
时,
或
;当
,
时,
,故点
。因此,l上至少含有一个D-点,即
。
由上述引理立即可得下述定理:
定理3.8:设直线
,则
当且仅当直线l不具有性质
。
定理3.9:设直线
,若直线l上含有D-点P,则有
(a)
当且仅当
。
(b)
当且仅当
。
证明:已知直线
上含有点
,令直线
,则
,于是
。
(a) 必要性:由于
,则直线l上必含不同于点P的D-点
。令点
,显然有点
,根据引理2.3可得点
,从而由引理2.4可得点
。因为
,所以
。于是由定理3.2可得
,进而根据定理3.4可得直线
的斜率即直线l的斜率
。
充分性:设直线l的斜率
,则由定理3.4可知
,于是根据推论3.3可得
,记直线
上的无穷多个
-点为
,令点
,则点
,又由引理2.4可得,点
与点
为同类D-点,因此
。
(b) 必要性:假设直线l的斜率
,由(a)可得此时
,与已知条件
矛盾,因此
。
充分性:假设
,由于直线l上含有D-点P,则直线l上必含不同于点P的D-点Q,而由(a)中必要性的证明过程可得,此时直线l的斜率
,与已知条件
矛盾,因此
。
综上所述,可得下述定理:
定理3.10:设直线
,则
当且仅当
(1) 直线l具有性质
;
(2)
。
定理3.11:设直线
,则
当且仅当
(1) 直线l具有性质
;
(2)
。
注3.12:直线
显然也具有性质
,从而定理3.4与定理3.5分别为定理3.10与定理3.11中
时的特殊情形。
对于含有D-点的直线
,其中
,必含无穷多个D-点。下面对直线l上D-点类型的分布进行讨论,并依据所含的D-点类型对此类直线进一步进行划分及刻画。
定理3.13:设直线
,其中
,
,则有
(a) 直线l上仅含无穷多个
-点当且仅当
;特别地,此时
。
(b)
,
当且仅当
;特别地,此时
。
(c)
,
当且仅当
;特别地,此时
。
证明:已知直线
,其中
,
,则由定理3.4可得直线l上必含无穷多个D-点。由
可得整数m与n或为两个奇数,或为一奇一偶,即有
或
。
(a) 必要性:令点
,则点P在直线l上。若
,则
,于是当
时点
;当
时点
。从而直线l上必含
-点或
-点,与条件直线l上仅含
-点矛盾,因此
。
充分性:设直线
,其中
,
且
,要证直线l上仅含无穷多个
-点,只需证直线l上不含其它类型的D-点。假设
,即可设直线l上含有
-点
,其中
,
,
,将其坐标代入直线方程可得
,即
。由于
与
均为奇数,而m与n必为一奇一偶,则乘积
与
必
为一奇一偶,二者不可能相等,产生矛盾,因此
。同理可证
。综上可得,直线l上仅含无穷多个
-点。
特别地,下证此时
。令点
,则易知点
且
,
,又由
可得
,从而点
。令点
,其中t为奇数,则易知点
,进而由引理2.2可得点
,因此
。
(b) 必要性:由于
,即直线l上不仅含
-点,则由(a)可得
。于是有
,此时
,从而有
或
。易验证点
在直线l上,若
,则点
,与已知条件
矛盾,因此
。
充分性:设直线
,其中
,
且
,易得
。对于点
有
且
。令点
,其中
,则点
。根据引理2.2可知,当λ为奇数时,点
;当
为偶数时,点
。因此
。假设
,即可设直线l上含
-点
,其中
,
且
,将其坐标代入直线方程可得
,即
。于是有
,即
。由于
,则
,而由
可得
,于是
,与已知条件
矛盾,因此
。综上可得
且
。
特别地,下证此时
。假设l上含有C-点
,其中
,
,
,将其坐标代入直线方程可得
,即
。于是有
,即
。由
可得
,又由
可得
,于是
,进而由
可得
,从而有
,与已知条件
矛盾,因此
。
情形(c)类似于情形(b)可证。
定理3.14:设直线
,其中
,
。若l上含有
-点
,则有
(a) 直线l上仅含无穷多个
-点当且仅当
。
(b)
,
当且仅当
。
(c)
,
当且仅当
。
证明:已知直线
上含有点
,令直线
,则
,于是
,即直线l可由直线
平移向量OP0得到。由引理2.4可知,直线l与
上D-点的类型及分布情况一致,进而根据定理3.13立即得证。
定理3.15:设直线
,其中
。若l上含有
-点
,则有
(a) 直线l上仅含无穷多个
-点当且仅当
。
(b)
,
当且仅当
。
(c)
,
当且仅当
。
证明:已知直线
上含有点
,令直线
,则
,于是
,即直线l可由直线
平移向量OP1得到。因此,可根据
上D-点的类型及分布情况,利用引理2.4讨论l上D-点的类型及分布情况。
(a) 由定理3.13可知
,
当且仅当
,且此时
,即
上除了
-点及
-点以外,其它点均为非T-点。由引理2.4可得,将直线
平移至直线l后,
上的
-点与
-点分别变为l上的
-点与C-点,而
上的其它点均变为l上的非T-点,亦为非D-点,于是直线l上仅含无穷多个
-点。因此,直线l上仅含无穷多个
-点当且仅当
。
(b) 由定理3.13可知
,
当且仅当
,且此时
,即
上除了
-点及
-点以外,其它点均为非T-点。由引理2.4可得,将
平移至l后,
上的
-点与
-点分别变为l上的
-点与
-点,而
上的其它点均变为l上的非T-点,亦为非D-点,于是
且
。因此
,
当且仅当
。
(c) 由定理3.13可知直线
上仅含无穷多个
-点当且仅当
,且此时
,即
上除了
-点及C-点以外,其它点均为非T-点。由引理2.4可得,将
平移至l后,
上的
-点与C-点分别变为l上的
-点与
-点,而
上的其它点均变为l上的非T-点,亦为非D-点,于是
且
。因此
,
当且仅当
。
类似地可得下述定理:
定理3.16:设直线
,其中
,
。若l上含有
-点,则有
(a) 直线l上仅含无穷多个
-点当且仅当
。
(b)
,
当且仅当
。
(c)
,
当且仅当
。
4.
方向上内部无D-点的最宽路径
通过对于任意直线上所含D-点数的讨论可知,存在不含D-点的直线。因而,可进一步探究是否存在由两条平行线所界定的带形区域满足其内部不含D-点,若存在那么进一步刻画其最大宽度。
定义4.1:设直线l与
是平面内倾斜角为
的两条平行直线,则称直线l与
所夹的带形区域为
方向上的路径,称直线l与
间的垂直距离为该路径的宽度。
注4.2:在三角格T中,
方向上内部不含T-点的路径的最大宽度记为
。在铺砌
中,
方向上内部不含D-点的路径的最大宽度记为
。
根据铺砌
的特征,显然有:
定理4.3:当
时,
;当
时,
。
当
时,按
是否具有形式
可以分为两种情形讨论。首先考虑
的情形,对于直线
,其中
,其至多含一个D-点,下面考虑l附近的D-点分布情况。
引理4.4 [2] :设α为任意的无理数, ,则存在一对整数
满足不等式
,则存在一对整数
满足不等式
(1)
类似地,存在另一对整数
满足不等式
(2)
定理4.5:设直线
,其中
,则对任意给定的
且
,在直线l的两侧均存在无穷多个D-点到直线l的距离小于ε。
证明:令
,
。因为
,所以
为无理数,显然
。下面根据k的取值分为两种情形。
情形1:
因为
,故存在
且满足
。令
,由引理4.4可得,存在一对整数
满足
,即
于是有
令点
,易知点
。设
到l的垂直距离与竖直距离分别为
和
(如图3),从而
,又由于
,所以点
在l的上方且满足
。
根据引理4.4可得,对于任意给定的实数
,均存在一对整数
满足不等式(1)。因此,对于任意给定的无穷递减序列
,可以运用上述的构造方法,给出无穷多个D-点
,满足每个
均在l的上方且到l的垂直距离
。因此证得在l的上方存在无穷多个D-点到l的距离小于ε。
另一方面,若在上述证明过程中用引理4.4中的不等式(2)替换不等式(1),则同理可得在l的下方存在无穷多个D-点到l的距离小于ε。
情形2:
由于
,不妨令
,根据情形1同理可证。
由上述定理分析可得,当
时,对于θ方向上的直线l而言,在其两侧均存在无穷多个D-点无限逼近l,故此时θ方向上不存在内部不含D-点的路径。
接下来考虑当
时,θ方向上内部不含D-点的最宽路径。
引理4.6:设直线
,其中
,若l上含有C-点,则
且
。
证明:不妨设直线
上含有C-点P,令直线
,则
,于是
,即直线l可由直线
平移向量OP得到。由于
,则根据定理3.13可得,
含无穷多个
-点,且含有无穷多个点
满足
。进而根据引理2.4可得,将直线
平移至直线l后,
上的
-点变为l上的C-点且
上的点
均变为l上的D-点,由此可得
且
。
定理4.7:设直线
,其中
,若直线l上含T-点,则l上必含D-点。
证明:不妨设直线l上含点
,则点
。若点
,则结论显然成立;否则,点
,由引理4.6可得,此时直线l上含D-点。因此直线l上必含D-点。
引理4.8 [5] :在三角格T中,设
,其中
,
,
。若m和n均
图3. 构造D-点
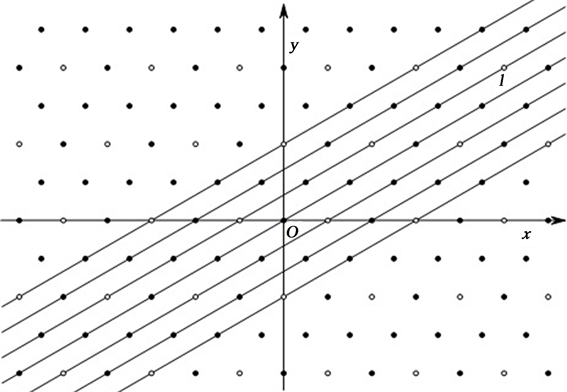
Figure 4. The broadest paths containing no D-points in their interiors
图4. 内部无D-点的最宽路径
为奇数,则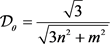 ;否则,
;否则,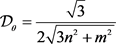 。
。
定理4.9:在铺砌
中,设
,其中
,
,
,则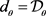 ,即
,即
.
证明:在铺砌
中,对于任意斜率为
的直线l,由定理4.7可知,若直线l上含T-点,则直线l上必含D-点。因此,在铺砌
中,θ方向上内部无D-点的路径的最大宽度即为θ方向上内部无T-点的路径的最大宽度(如图4),故 。由引理4.8可得,当m和n均为奇数时,
。由引理4.8可得,当m和n均为奇数时, ;当m和n有一个为偶数时,
;当m和n有一个为偶数时, 。
。
文章引用
彭琳,苑立平. 铺砌(3.6.3.6)中直线上的D-点数
On the Number of D-Points on a Line in the Tiling (3.6.3.6)[J]. 应用数学进展, 2017, 06(07): 905-916. http://dx.doi.org/10.12677/AAM.2017.67109
参考文献 (References)
- 1. Grünbaum, B. and Shephard, G.C. (1987) Tilings and Patterns. W. H. Freeman and Company, New York.
- 2. Olds, C.D., Lax, A. and Davidoff, G.P. (2001) The Geometry of Numbers. The Mathematical Association of America, Washington.
- 3. Cao, P. and Yuan, L. (2014) The Number of Lattice Points and T-Points on a Line in . Southeast Asian Bulletin of Mathematics, 38, 21-25.
- 4. 常之魁, 李英姿. 铺砌(33.42)中直线上的D-点数[J]. 数学杂志, 2013, 33(2): 359-362.
- 5. 曹鹏浩. 关于H-点相关问题的研究[D]: [硕士学位论文]. 石家庄: 河北师范大学, 2010.







 ,则存在一对整数
满足不等式
,则存在一对整数
满足不等式

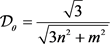 ;否则,
;否则,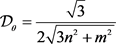 。
。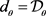 ,即
,即 。由引理4.8可得,当m和n均为奇数时,
。由引理4.8可得,当m和n均为奇数时, ;当m和n有一个为偶数时,
;当m和n有一个为偶数时, 。
。