ABSTRACT

In this paper, we present a high speed compressible lattice Boltzmann model coupled with Lee-Tarver reaction rate function for detonation. Two distribution functions are used to describe the density, momentum and energy of reactant and product in the lattice Boltzmann scheme, which gives consistent results with the Navier-Stokes equation in the continuum limit. Due to the separation of time scales in the chemical and thermodynamic process, the operator-splitting scheme is employed to solve Lee-Tarver reaction rate function. To indicate the validity of the model, we studied the collision between detonation and shock waves, the Richtmyer-Meshkov instability by detonation. The numerical examples show that the scheme can be used to compute the detonation phenomena.

Keywords:Lattice Boltzmann Model, Detonation, Richtmyer-Meshkov Instability, Lee-Tarver Reaction Rate Function

基于格子Boltzmann模型的Lee-Tarver爆轰波计算

闫铂，王建朝

吉林建筑大学土木工程学院，吉林 长春

收稿日期：2017年11月28日；录用日期：2017年12月14日；发布日期：2017年12月21日

摘 要

本文提出了高速可压格子Boltzmann模型与Lee-Tarver反应率函数相耦合的模型求解爆轰问题。格子Boltzmann模型使用两个平衡态分布函数分别描述反应物和产物的密度、动量和能量。在连续极限假设下，模型能够给出与Navier-Stokes方程一致的结果。由于化学反应过程和热动力学过程的时间尺度是分离的，所以采用算子分裂法求解Lee-Tarver反应率函数。为了验证模型的有效性，我们研究了爆轰波与冲击波的对撞问题以及爆轰波引发的Richtmyer-Meshkov不稳定性问题。数值结果表明，本文所提出的模型可以用来模拟爆轰现象。

关键词 :格子Boltzmann模型，爆轰，Richtmyer-Meshkov不稳定性，Lee-Tarver反应率函数

Copyright © 2017 by authors and Hans Publishers Inc.

This work is licensed under the Creative Commons Attribution International License (CC BY).

http://creativecommons.org/licenses/by/4.0/

1. 引言

爆轰是通过冲击波传播的超声速燃烧。爆轰过程释放巨大能量，爆轰波扫过的介质成为高温高压的爆轰产物。模拟爆轰系统的方法主要是求解Naiver-Stokes方程和化学反应方程相耦合的方程组，有追踪法 [1] [2] [3] 、Arbitrary Lagrange-Euler法 [4] [5] 、level set法 [6] [7] 、Volume of Fluid法 [8] 等。随着格子Boltzmann方法在高速可压流体系统建模中取得一系列进展，使得格子Boltzmann模型模拟冲击与爆轰问题成为可能 [9] - [15] 。

本文采用高速可压格子Boltzmann模型与Lee-Tarver反应率模型相耦合的方法求解爆轰问题。在格子Boltzmann模型中，使用两个平衡态分布函数分别描述反应物和产物的密度、动量和能量。在连续极限下，该模型可以恢复Navier-Stokes方程。由于爆轰过程中化学反应时间的尺度比宏观流动的时间尺度小几个数量级，因此采用算子分裂法求解Lee-Tarver反应率函数。该模型突破了化学反应对流场没有影响的限制，实现了化学反应和流场的自然耦合。数值结果表明，本文所提出的模型能够用来模拟爆轰现象。

2. 格子Boltzmann模型

2.1. 描述宏观流动的格子Boltzmann模型

本文采用双组份格子Boltzmann模型描述爆轰的宏观流动过程。其离散速度模型使用文献 [16] 所提出的D2V33模型。D2V33模型具有33个离散速度，能够满足恢复Navier-Stokes方程所需的七阶各向同性。其中，

$\{\begin{array}{l}{v}_0=0,\\ v_{ki}=v_k\left[cos\left(i\text{π}/4\right),sin\left(i\text{π}/4\right)\right].\end{array}$ (1)

下标 $k=1,2,3,4$ 表示第 $k$ 组粒子速度是 $v_k$ ，本文选取 $v_1=1.00$ 、 $v_2=1.92$ 、 $v_3=2.99$ 、 $v_4=4.49$ ； $i=1,2,\cdots ,8$ 表示粒子速度方向。

分布函数 $f_{ki}^{\sigma }$ 遵循以下格子Boltzmann方程：

$\frac{\partial f_{ki}^{\sigma }}{\partial t}+v_{ki}\cdot \frac{\partial f_{ki}^{\sigma }}{\partial r}=-\frac{1}{{\tau }^{\sigma }}\left[f_{ki}^{\sigma }-f_{ki}^{\sigma ,eq}\right]$ . (2)

其中 $\sigma \in \left(r,p\right)$ ，分别代表反应物和产物； $r$ 表示空间坐标； ${\tau }^{\sigma }$ 为 $\sigma$ 组份的松弛因子； $\sigma$ 组份的局域平衡态分布函数 $f_{ki}^{\sigma ,eq}$ 由下式给出

$\begin{array}{c}{f}_{ki}^{\sigma ,eq}={\rho }^{\sigma }{F}_k\{\left[1-\frac{u^2}{2T}+\frac{u^4}{8T^2}\right]+\frac{v_{ki\epsilon }{u}_{\epsilon }}{T}\left(1-\frac{u^2}{2T}\right)+\frac{v_{ki\epsilon }{v}_{ki\pi }{u}_{\epsilon }{u}_{\pi }}{2T^2}\left(1-\frac{u^2}{2T}\right)\\ +\frac{v_{ki\epsilon }{v}_{ki\pi }{v}_{ki\upsilon }{u}_{\epsilon }{u}_{\pi }{u}_{\upsilon }}{6T^3}+\frac{v_{ki\epsilon }{v}_{ki\pi }{v}_{ki\upsilon }{v}_{ki\xi }{u}_{\epsilon }{u}_{\pi }{u}_{\upsilon }{u}_{\xi }}{24T^4}\}.\end{array}$ (3)

在(3)式中， ${\rho }^{\sigma }$ 表示 $\sigma$ 组份的密度； $u$ 表示局域平均速度，有

$u=\frac{{\rho }^r{u}^r+{\rho }^p{u}^p}{{\rho }^r+{\rho }^p}$ ； (4)

$T$ 表示局域平均温度，有

$T=\frac{{\rho }^r{T}^r+{\rho }^p{T}^p}{{\rho }^r+{\rho }^p}$ ； (5)

权重因子 $F_k$ 和 $F_0$ 与文献 [13] [17] 一致。

为了在连续极限下得到与恢复Navier-Stokes方程一致的结果， $\sigma$ 组份的局域平衡态分布函数 $f_{ki}^{\sigma ,eq}$ 需要满足以下矩关系

${\displaystyle \sum _{ki}{f}_{ki}^{\sigma ,eq}}={\rho }^{\sigma }$ , (6)

${\displaystyle \sum _{ki}{v}_{ki}{f}_{ki}^{\sigma ,eq}}={\rho }^{\sigma }{u}^{\sigma }$ , (7)

${\displaystyle \sum _{ki}\frac{1}{2}{v}_{vi}^2{f}_{ki}^{\sigma ,eq}}=e_{therm}^{\sigma }+\frac{1}{2}{\rho }^{\sigma }{\left(u^{\sigma }\right)}^2={\rho }^{\sigma }{T}^{\sigma }+\frac{1}{2}{\rho }^{\sigma }{\left(u^{\sigma }\right)}^2=P^{\sigma }+\frac{1}{2}{\rho }^{\sigma }{\left(u^{\sigma }\right)}^2$ , (8)

${\displaystyle \sum _{ki}{v}_{ki\alpha }{v}_{ki\beta }{f}_{ki}^{\sigma ,eq}}=e_{therm}^{\sigma }{\delta }_{\alpha \beta }+{\rho }^{\sigma }{u}_{\alpha }^{\sigma }{u}_{\beta }^{\sigma }$ , (9)

${\displaystyle \sum _{ki}{v}_{ki\alpha }{v}_{ki\beta }{v}_{ki\gamma }{f}_{ki}^{\sigma ,eq}}=e_{therm}^{\sigma }\left(u_{\gamma }^{\sigma }{\delta }_{\alpha \beta }+u_{\alpha }^{\sigma }{\delta }_{\beta \gamma }+u_{\beta }^{\sigma }{\delta }_{\gamma \alpha }\right)+{\rho }^{\sigma }{u}_{\alpha }^{\sigma }{u}_{\beta }^{\sigma }{u}_{\gamma }^{\sigma }$ ,(10)

${\displaystyle \sum _{ki}\frac{1}{2}{v}_k^2{v}_{ki\alpha }{f}_{ki}^{\sigma ,eq}}=2e_{therm}^{\sigma }{u}_{\alpha }^{\sigma }+\frac{1}{2}{\rho }^{\sigma }{\left(u^{\sigma }\right)}^2{u}_{\alpha }^{\sigma }$ , (11)

${\displaystyle \sum _{ki}\frac{1}{2}{v}_k^2{v}_{ki\alpha }{v}_{ki\beta }{f}_{ki}^{\sigma ,eq}}=\left[2T^{\sigma }+\frac{1}{2}{\left(u^{\sigma }\right)}^2\right]e_{therm}^{\sigma }{\delta }_{\alpha \beta }+\left[3e_{therm}^{\sigma }+\frac{1}{2}{\rho }^{\sigma }{\left(u^{\sigma }\right)}^2\right]u_{\alpha }^{\sigma }{u}_{\beta }^{\sigma }$ . (12)

首先，通过(6)~(8)式计算 $\sigma$ 组份的密度 ${\rho }^{\sigma }$ 、速度 $u^{\sigma }$ 、压力 $P^{\sigma }$ 和温度 $T^{\sigma }$ 。当 $r$ 组份(反应物)和 $p$ 组份(产物)处于平衡状态时，通过(3)式计算 $\sigma$ 组份( $r$ 和 $p$ )的局域平衡态分布函数 $f_{ki}^{\sigma ,eq}$ ，并使用共同的局域平均速度 $u$ 和局域平均温度 $T$ 。在双组份流动系统中， $r$ 组份(反应物)和 $p$ 组份(产物)的粒子通过碰撞过程交换动量和能量，相对应的分布函数 $f_{ki}^r$ 和 $f_{ki}^q$ 不是相互独立的，而是通过两个格子Boltzmann方程耦合。分布函数 $f_{ki}^{\sigma }$ 通过松弛时间松弛到局域平衡状态，在求解 $f_{ki}^{\sigma ,eq}$ 过程中，即在(3)式中使用相同的局域平均速度 $u$ 和局域平均温度 $T$ 实现两个格子Boltzmann方程的耦合。

将方程(2)的左端用Lax-Wendroff有限差分格式离散，右端添加色散项和附加粘性项，并用二阶中心差分格式离散，得到以下形式的有限差分格子Boltzmann方程 [17] ：

$\begin{array}{c}{f}_{kiI}^{\sigma ,new}=f_{kiI}^{\sigma }-\frac{c_{ki\alpha }}{2}\left(f_{kiI+1}^{\sigma }-f_{kiI-1}^{\sigma }\right)-\frac{\Delta t}{\tau }\left(f_{kiI}^{\sigma }-f_{kiI}^{\sigma ,eq}\right)+\frac{c_{ki\alpha }^2}{2}\left(f_{kiI+1}^{\sigma }-2f_{kiI}^{\sigma }+f_{kiI-1}^{\sigma }\right)\\ +\frac{c_{ki\alpha }\left(1-c_{ki\alpha }^2\right)}{12}\left(f_{kiI+2}^{\sigma }-2f_{kiI+1}^{\sigma }+2f_{kiI-1}^{\sigma }-f_{kiI-2}^{\sigma }\right)+\frac{{\theta }_{\alpha I}^{\sigma }\left|k_{\alpha }^{\sigma }\right|\left(1-\left|k_{\alpha }^{\sigma }\right|\right)}{2}\left(f_{kiI+1}^{\sigma }-2f_{kiI}^{\sigma }+f_{kiI-1}^{\sigma }\right).\end{array}$ (13)

其中， $c_{ki\alpha }=v_{ki\alpha }\Delta t/\Delta r_{\alpha }$ ； $k_{\alpha }^{\sigma }=u_{\alpha }^{\sigma }\Delta t/\Delta r_{\alpha }$ ；； ${\theta }_{\alpha I}^{\sigma }={\eta }^{\sigma }\left|\frac{P_{\alpha I+1}^{\sigma }-2P_{\alpha I}^{\sigma }+P_{\alpha I-1}^{\sigma }}{P_{\alpha I+1}^{\sigma }+2P_{\alpha I}^{\sigma }+P_{\alpha I-1}^{\sigma }}\right|$ ； $I-2$ 、 $I-1$ 、 $I$ 、 $I+1$ 、 $I+2$ 代表 $x$ 或 $y$ 方向的5个连续点。修正的Lax-Wendroff有限差分格式是单调的守恒格式，能够改善数值稳定性。方程(13)中的“ $\frac{{\theta }_{\alpha I}^{\sigma }\left|k_{\alpha }^{\sigma }\right|\left(1-\left|k_{\alpha }^{\sigma }\right|\right)}{2}\left(f_{kiI+1}^{\sigma }-2f_{kiI}^{\sigma }+f_{kiI-1}^{\sigma }\right)$ ”项为附加粘性项，使模型既适用于低速不可压缩流体，又适用于高Mach数系统，使模型能够用于稳定冲击与爆轰问题。

2.2. 描述化学反应的Lee-Tarver反应率函数

爆轰中的化学反应过程相当复杂，选用恰当的化学反应率函数是关键，因为化学反应率函数能够决定爆轰的点火、发展和传播过程。Lee-Tarver反应率函数是与实验数据拟合最好的化学反应模型之一 [18] 。本文使用的Lee-Tarver反应率函数和初始条件如下：

$\frac{\text{d}\lambda }{\text{d}t}=\{\begin{array}{l}a\left(1-\lambda \right)+b\left(1-\lambda \right)\lambda ,T\ge T_{th},且0\le \lambda \le 1\\ 0,其它\end{array}$ (14)

其中， $\lambda$ 表示产物的组份数， $a$ 、 $b$ 为常数， $T_{th}$ 为化学反应的温度阈值。

由于爆轰化学反应的时间非常快，比宏观流动的时间小几个数量级，所以化学反应和宏观流动不能用同一时间尺度描述。为此，采用算子分裂法求解方程(14)，即将化学反应过程分为两步：

首先计算对流过程，

$\frac{\partial \lambda }{\partial t}+u\nabla \lambda =0$ (15)

并使用迎风格式计算，即

$\frac{{\lambda }_I^{n+1}-{\lambda }_I^n}{\Delta t}=-\{\begin{array}{l}\frac{u\left({\lambda }_I^n-{\lambda }_{I-1}^n\right)}{\Delta x},u\ge 0\\ \frac{u\left({\lambda }_{I+1}^n-{\lambda }_I^n\right)}{\Delta x},u<0\end{array}$ (16)

其中， $I-1$ 、 $I$ 、 $I+1$ 代表 $x$ 或 $y$ 方向的3个连续点。

然后计算化学反应过程

$\frac{\partial \lambda }{\partial t}=a\left(1-\lambda \right)+b\left(1-\lambda \right)\lambda$ , (17)

式(17)的解析解为

${\lambda }_I^{n+1}=\frac{{\text{e}}^{\left(a+b\right)\Delta t}+a\left({\lambda }_I^n-1\right)/\left(a+b{\lambda }_I^n\right)}{{\text{e}}^{\left(a+b\right)\Delta t}+b\left(1-{\lambda }_I^n\right)/\left(a+b{\lambda }_I^n\right)}$ . (18)

2.3. 化学反应与流动的耦合

在真实的燃烧过程中，化学反应放出的热量和内能是耦合的。化学反应放出热量必然导致内能增加，内能的增加引起压强的变化，进而影响密度和流速的变化。在本文所构建的双组份格子Boltzmann模型中，总的内能 $\dot{e}$ 由化学反应产生的内能 ${\dot{e}}_{chem}$ 和热力学内能 ${\dot{e}}_{therm}$ 两部分组成

$\dot{e}={\dot{e}}_{therm}+{\dot{e}}_{chem}$ , (19)

${\dot{e}}_{chem}=\dot{\lambda }\rho Q$ . (20)

其中， $Q$ 是单位质量反应物发生化学反应放出的热量，局域平均密度 $\rho ={\rho }^r+{\rho }^p$ 。

在数值模拟中，首先通过(5)式计算热力学部分的内能 $e_{therm}$ ，然后通过(19)~(20)式计算总的内能 $e$ ；再用总内能 $e$ 替代 $e_{therm}$ 并更新压力 $P$ 和温度 $T$ ；最后更新反应物和产物的密度，即

${\rho }^{r,new}={\rho }^r-\dot{\lambda }\rho$ ,(21)

${\rho }^{p,new}={\rho }^p+\dot{\lambda }\rho$ .(22)

通过这样的过程，化学反应和流场实现了自然耦合。

3. 数值例子

例1：首先考虑一均匀充满可燃气体的刚性长管，左端为稳定爆轰波，右端为冲击波。假设冲击波的强度不足以引爆可燃气体，即冲击波波阵面后的温度低于可燃气体发生化学反应的温度阈值。首先，爆轰波和冲击波分别沿着各自传播方向运动，瞬时完成了冲击波和爆轰波前导冲击波的相交，由于熵值不同，两波之间形成一道接触间断；在接触间断的左侧，透射冲击波与燃烧产物相互作用；在接触间断的右侧，透射爆轰波的前导冲击波与可燃气体相互作用，可燃气体受到压缩，发生化学反应。

左边界爆轰波的初值为 ${\left(\rho ,u,v,T,\lambda \right)}_L={\left(1.42,1.52,0,6.12,1.00\right)}_L$ ，即爆轰波的Ma数为3.5；右边界冲击波的Ma数为1.5，其初值可以根据冲击波Hugoniot关系和强度计算。其它参数为：空间步长 $\Delta x=\Delta y=0.001$ 、 ${\tau }^{\sigma }={10}^{-5}$ 、 $Q=3.5$ 、绝热指数 $\gamma =2.0$ 、化学反应温度阈值 $T_{th}=3.8$ 、网格数 $N_x\times N_y=1000\times 3$ ；Lee-Tarver反应率函数中的参数为 $a=1$ 、 $b={10}^3$ 。

爆轰波的Hugoniot关系为

${\rho }_0\left(D-u_0\right)={\rho }_1\left(D-u_1\right)$ , (23)

$P_1-P_0={\rho }_0\left(D-u_0\right)\left(u_1-u_0\right)$ , (24)

$e_1-e_0=0.5\left(P_1+P_0\right)\left(1/{\rho }_0-1/{\rho }_1\right)+\lambda Q$ . (25)

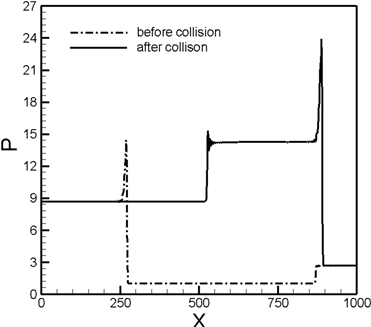
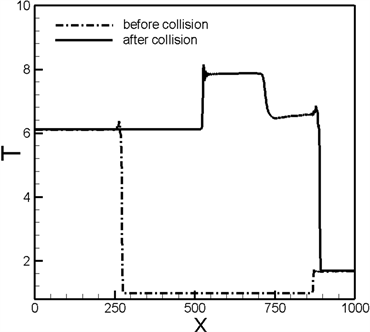
图1(a)~图1(d)给出了爆轰波与冲击波对撞前后的物理量密度 $\rho$ 、压力 $P$ 、流速 $u$ 、温度 $T$ 的变化曲线。图中可以清晰地观测到爆轰波的von Neumann峰、化学反应区和Taylor稀疏波等基本特征。

为了验证模型的有效性，我们计算了对撞后透射爆轰波的Hugoniot关系和透射冲击波的Hugoniot关系。从图1中，测得入射爆轰波和入射冲击波的速度分别为5.0和−2.1；透射爆轰波和透射冲击波的速度分别为4.5和−2.7。将透射爆轰波前后的各物理量带入方程(23)~(25)两侧进行计算，表1给出了透射爆轰波前后的Hugoniot关系以及方程右侧对左侧的偏差。同样地，我们将透射冲击波前后的各物理量带入冲击波的Hugoniot关系，即方程(23)~(25)中 $\lambda Q=0$ 时所得的方程，表2给出了透射冲击波前后的Hugoniot关系以及方程右侧对左侧的偏差。以上数值结果充分表明，本文所提出的格子Boltzmann模型符合爆轰波/冲击波的Hugoniot关系，可以用于爆轰/冲击问题的模拟。

例2：Richtmyer-Meshkov(R-M)不稳定性是冲击波加速两种密度不同的分层流体所导致的界面失稳现象。我们使用本文所提出的格子Boltzmann模型研究了爆轰波从轻流体进入重流体时的R-M不稳定性。

考虑一爆轰管，里面均匀充满可燃气体。爆轰波从左侧进入，其前端为前导冲击波，前导冲击波后跟随一化学反应区。前导冲击波使可燃气体受到压缩，温度升高，当温度超过发生化学反应的温度阈值时引爆可燃气体，释放热量并支持前导冲击波。初始状态为：

${\left(\rho ,u,v,T,\lambda \right)}_L={\left(1.26,0.35,0,1.26,0\right)}_L$ ,

${\left(\rho ,u,v,T,\lambda \right)}_M={\left(1,0,0,1,0\right)}_M$ ,

${\left(\rho ,u,v,T,\lambda \right)}_R={\left(5.04,0,0,0.19,0\right)}_R$ .

下标L、M、R分别表示计算域左侧、中间、右侧部分。空间步长 $\Delta x=\Delta y=0.001$ 、时间步长 $\Delta t={10}^{-5}$ 、绝热指数 $\gamma =2.0$ 、化学反应温度阈值 $T_{th}=1.1$ 、网格数 $N_x\times N_y=600\times 100$ ；Lee-Tarver反应率函数中的参数为 $a=1$ 、 $b={10}^3$ 。初始界面扰动为 $x=0.15\times N_x\times \Delta x+8\times {10}^{-3}\cos \left(40\text{π}y\right)$ ，即初始扰动界面平均位置为0.15，初始扰动的周期为0.05，振幅为 $8\times {10}^{-3}$ 。在数值模拟中，左侧边界采用入流边界条件，右侧边界采用出流边界条件；上侧和下侧边界采用周期边界条件。

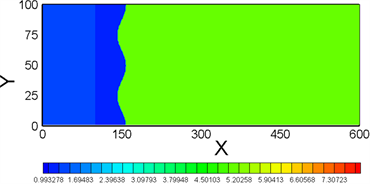
图2给出了t = 0、0.05、0.2、和1.0时刻密度等值线图。从图中可以看出，在t = 0.05时刻，爆轰波的前导冲击波与界面相互作用后，形成一列向左的反射冲击波和一列向右的透射爆轰波。刚扫过界面的透射爆轰波具有一定的曲率，由于压缩作用，界面产生了一个较小的变形，振幅略有减小；在t = 0.2时刻，反射冲击波已经出了计算区域，透射爆轰波阵面趋于平缓，说明透射爆轰波是稳定的。钉子结构内

图1. 爆轰波与冲击波对撞前后各物理的变化曲线。(a) 密度 $\rho$ ，(b) 压力 $P$ ，(c) x方向的速度分量 $u$ ，(d) 温度 $T$

表1. 透射爆轰波前后的Hugoniot关系

表2. 透射冲击波前后的Hugoniot关系

图2. 爆轰波由轻流体流入重流体时引发的Richtmyer-Meshkov不稳定性的密度等值线快照。(a) t = 0, (b) t = 0.05, (c) t = 0.2, (d) t = 1.0

部的压强大于外部压强，在压强差的作用下界面扰动振幅开始逐渐增加，并缓慢地形成了由右侧重流体流向左侧轻流体的钉子结构和左侧轻流体进入右侧重流体的泡状结构，与文献 [19] [20] 相类似。

4. 结论

本文构造了用于模拟爆轰问题的完全可压缩格子Boltzmann模型：流场采用双组份格子Boltzmann模型描述，化学反应采用Lee-Tarver反应率函数描述，实现了化学反应与流体流动过程的自然耦合。由于化学反应和宏观流动不能用同一时间尺度描述，因此采用算子分裂法求解化学反应率方程。为了验证模型的有效性，模拟研究了爆轰波与冲击波的对撞和爆轰波引发的Richtmyer-Meshkov不稳定性问题。数值结果充分表明，本文所提出的模型能够用来模拟冲击起爆和热起爆的基本过程，能够准确描述爆轰的von Neumann峰、化学反应区、Taylor稀疏波等基本特征。

基金项目

感谢闫广武教授、许爱国研究员、张广财研究员的建议、讨论和各类帮助。感谢国家自然科学基金(NO. 51406067, NO. 11272133)，吉林省教育厅科研项目(吉教科合字[2016]第141号)资助。

文章引用

闫 铂,王建朝. 基于格子Boltzmann模型的Lee-Tarver爆轰波计算
The Computation of Lee-Tarver Detonation Based on Lattice Boltzmann Model[J]. 应用数学进展, 2017, 06(09): 1126-1134. http://dx.doi.org/10.12677/AAM.2017.69137

参考文献 (References)