Advances in Applied Mathematics
Vol.07 No.07(2018), Article ID:25984,6
pages
10.12677/AAM.2018.77101
Critical Groups of Zeros for a Quasilinear Elliptic Equation
Zhenting Wang*, Mingshuang Duan, Weiwei Li, Yaqiong Wang
College of Sciences, North China University of Technology, Beijing

Received: Jun. 23rd, 2018; accepted: Jul. 13th, 2018; published: Jul. 20th, 2018

ABSTRACT
In this paper, we will study a class of quasilinear elliptic equations by Morse theory. Compared with the existing results, our new contents include two aspects: we first get the isolation of the zero when the nonlinear is resonant. Secondly, the critical groups for the zero are obtained under the weak condition.
Keywords:Quasilinear Elliptic Equations, Resonance, Morse Theory
一类拟线性椭圆方程零点的临界群
王振婷*,段明双,李微微,王亚琼
北方工业大学理学院,北京

收稿日期:2018年6月23日;录用日期:2018年7月13日;发布日期:2018年7月20日

摘 要
本文使用Morse理论来研究一类拟线性椭圆方程,与已有的结果相比,我们内容包含两个新的方面:一是在非线性项共振时证明了零点的孤立性,二是在弱的条件下计算出了零点的临界群。
关键词 :拟线性椭圆方程,共振,Morse理论

Copyright © 2018 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
拟线性椭圆型方程有很好的应用背景,比如在物理上可以用来研究非牛顿流体、孤立波的传播现象及非线性弹性问题等(请参考文献 [1] )。Morse理论是目前研究具有变分结构的椭圆型方程可解性最常用的工具之一,已经在半线性椭圆方程的研究中发挥了重要的作用。使用Morse理论时,需要刻画方程对应的泛函在其孤立临界点附近的局部拓扑性质,以及泛函整体拓扑性质,并运用Morse等式等工具来得到方程非平凡解的存在性以及解的各种几何性质。但是,人们若想利用Morse理论来研究拟线性方程临界点的性质,就会产生许多技术性的困难,比如,泛函对应的空间不再是具有正交分解的Hilbert空间,而是一般的Banach空间,许多经典的理论如Gromoll-Meyer定理和Morse引理不再成立,等等。这就要求人们不断的去完善并拓展已有的工具,推广已有的理论方法,得到新的应用范围更广的临界点理论。
2. 已有结果与本文定理
假设 是边界光滑的有界区域,本文研究下面的拟线性椭圆方程
(P)
这里 ;特别地,当 时, 为经典的拉普拉斯算子。
假定非线性项满足下面的条件:
(f1) 并且
这里 是一个常数, ,其中 如果 , 如果 。使用于(f1),由文献 [2] 可知方程(P)的弱解等价于 泛函 的临界点,这里I定义如下
其中 , 的范数定义为
本文拟使用Morse理论和变分方法来研究我们的方程(P),因此我们首先给出所需的定义以及一些预备知识(请看文献 [3] [4] )。设空间E是Banach空间, 是 泛函。我们约定以下记号:
。
下面是基本的紧性条件:
定义1.1:假设泛函 ,若任何满足 有界, 的序列 都有收敛子列,则称J满足Palais-Smale (简称(PS))条件。
我们用
表示拓扑对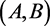 的q阶相对奇异同调群,其系数用G表示。
的q阶相对奇异同调群,其系数用G表示。
定义1.2:设 为J的一个孤立临界点 ,U是 的领域,使得 是J在U中唯一的临界点。我们称相对奇异同调群
是J在 处的q阶临界群。
下面列举方程(P)已有的一些结果。假设
是算子 在空间
中的特征值。如果
在空间
中的特征值。如果
(g1) ,满足
,
那么根据文献 [5] 得到
。
另外,在下面的共振条件下,
(g2) ,满足 及存在常数 使得
,
文章 [6] 使用局部环绕以及有限维约化的方法得到
。
其它类似的结果请参考文献 [5] [7] 。
本文主要是减弱文章 [6] 中的条件,但能得到更多的结果。假设
,
满足下面条件:
(f2) ,并且存在常数 , 及 使得
。
本文的结果如下。
定理1.1:如果条件(f1)与(f2)成立,那么 为泛函I的孤立临界点,并且
。
注:1) 本文主要使用临界群的同伦不变性来证明定理,因此我们的泛函根据条件(f1)只需要是 的,而文章 [6] 中的泛函要求是 光滑;
2) 在之前的文章中,为了使用临界群,一般都是假设零点是孤立的临界点,而在我们的结果中可以证明此结论;
3) 根据条件(f2),可以推出存在常数 使得
,
因此我们的条件比(g2)的范围更广;总之,我们的定理是新的。
3. 定理的证明
由文章 [6] 中的结果知泛函I在有界闭集上满足(PS)条件,所以零点临界群的定义有意义。在不引起混淆的情况下,下面我们都用C表示不同的正常数。
引理1.2:如果(f1)与(f2)成立,那么 为泛函I的孤立临界点。
证:反设存在非零元素 使得 ,即 为泛函的非零临界点,由椭圆方程的正则性估计( [5] )得到
,
所以当n充分大时 ,再由(f2)得到
。
根据特征值的定义及 得到
根据 ,当n充分大时有 ,此时上式表明
,
此矛盾推出 为泛函I的孤立临界点。证毕。
为了计算零点的临界群,我们需要下面的临界群的同伦不变性定理。
命题1.3:( [8] )设X为Banach空间, ,其中 ,并且 为泛函列 的共同临界点。如果存在 的一个邻域U使得
1) 在邻域U中满足(PS)条件;
2) 对于 , 是 在邻域U中的唯一临界点;
3) 算子 是 光滑的;
那么我们有
。
类似于文章 [9] ,对于 ,我们首先定义一个函数 如下
并定义泛函 为
,
其中G为 的原函数。明显地, 。
引理1.4:如果(f1)与(f2)成立,那么对于任意的 , 为泛函 的孤立临界点。
证:反设存在 及 使得 为泛函 的非零临界点,即有 ,再由椭圆方程的正则性估计得到
,
所以当n充分大时 ,此时得到
,
所以
,
即 为泛函I的非零临界点,这与引理1.2矛盾。证毕。
引理1.5:如果(f1)与(f2)成立,那么
证:根据 的定义可知
,
所以根据(f2)得到
因为 ,当 充分小时 ,即零点为泛函 的局部极小,如此根据文献 [3] 得到我们的结论。证毕。
证明定理1.1:使用引理1.2,我们得到 为泛函I的孤立临界点。对于任意的 ,条件(f1)保证了泛函 在任何的有界区域上都满足(PS)紧性条件,并且算子 是 光滑的;另外,引理1.4说明 为泛函 的孤立临界点。
综上所述,使用命题1.3和引理1.5,我们有
,
定理证明完毕。
4. 结语
近十几年来,拟线性椭圆方程是非线性分析方向的一个热点问题,不仅因为此类方程有很好的物理生物背景,更重要的是人们发现以往处理半线性椭圆问题的工具,比如极小极大方法、上下解方法、Morse理论等,并不能直接的平移到拟线性椭圆方程中,这就给此类问题的研究带来了极大的挑战,它要求人们不断的去完善并拓展已有的工具。在无穷维Morse理论中,用两类整数来刻划泛函在其孤立临界点附近的局部拓扑性质和泛函定义域的整体拓扑性质。本文中只是研究了泛函在零点的性质,如果还能得到方程在无穷远处的几何结构,我们还可以得到方程非平凡解的存在性,这也是我们今后要研究的问题。另外,我们期望本文所得到结果和方法发展到其它变分问题上,如椭圆系统、Hamilton系统等。
基金项目
北京市教育委员会科技计划一般项目(KM201710009012)、北方工业大学基金。
文章引用
王振婷,段明双,李微微,王亚琼. 一类拟线性椭圆方程零点的临界群
Critical Groups of Zeros for a Quasilinear Elliptic Equation[J]. 应用数学进展, 2018, 07(07): 842-847. https://doi.org/10.12677/AAM.2018.77101
参考文献
- 1. Benci, V., Fortunato, D. and Pisani, L. (1998) Soliton-Like Solutions of a Lorentz Invariant Equation in Dimension 3. Journal of Mathematical Physics, 3, 315-344. https://doi.org/10.1142/S0129055X98000100
- 2. Dinca, G., Jebelean, P. and Mawhin, J. (2001) Variational and Topological Methods for Dirichlet Problems with p Laplacian. Portugal. Math. (N.S), 58, 339-378.
- 3. Chang, K. (1993) Infinite Dimensional Morse Theory and Multiple Solution Problems. Birkhauser. https://doi.org/10.1007/978-1-4612-0385-8
- 4. 张恭庆. 临界点理论及其应用[M]. 上海: 上海科学技术出版社, 1986.
- 5. Cingolani, S. and Vannella, G. (2003) Critical Groups Computations on a Class of Sobolev Banach Spaces via Morse Index. Annales de l’Institut Henri Poincare. Analyse Non Lineaire, 20, 271-292. https://doi.org/10.1016/S0294-1449(02)00011-2
- 6. Sun, M.Z., Zhang, M.L. and Su, J.B. (2015) Critical Groups at Zero and Multiple Solutions for a Quasilinear Elliptic Equation. Journal of Mathematical Analysis and Applications, 428, 696-712. https://doi.org/10.1016/j.jmaa.2015.03.033
- 7. Sun, M. (2012) Multiplicity of Solutions for a Class of the Quasilinear Elliptic Equations at Resonance. Journal of Mathematical Analysis and Applications, 386, 661-668. https://doi.org/10.1016/j.jmaa.2011.08.030
- 8. Chang, K.-C. and Ghoussoub, N. (1996) The Conley Index and the Critical Groups via an Extension of Gromoll-Meyer Theory. Topol. Methods Nonlinear Analysis, 7, 77-93. https://doi.org/10.12775/TMNA.1996.003
- 9. Iannizzotto, A., Liu, S., Perera, K. and Squassina, M. (2016) Existence Results for Fractional p-Laplacian Problems via Morse Theory. Advances in Calculus of Variations, 9, 101-125. https://doi.org/10.1515/acv-2014-0024