Advances in Applied Mathematics
Vol.
08
No.
03
(
2019
), Article ID:
29287
,
15
pages
10.12677/AAM.2019.83054
Dynamic Scheduling Strategy of Smart RGV Based on Matrix Cycle
Yang Gu*#, Zhourong Zhang†, Jin Jiang†
College of Science, Nanjing University of Aeronautics and Astronautics, Nanjing Jiangsu

Received: Feb. 28th, 2019; accepted: Mar. 12th, 2019; published: Mar. 19th, 2019

ABSTRACT
This paper mainly studies the dynamic scheduling problem of a smart RGV. For the processing operation of one process, it is judged by simulation analysis that the cyclic cycle scheduling is the optimal scheduling. Therefore, we establish an optimal scheduling model based on matrix cycle, and transform the path planning into a traveling salesman problem (TSP). Then we use Lingo and MATLAB to solve three sets of parameters, the total number of workpiece production is 384, 347, and 395, respectively, and the system operation efficiency is as high as 98%. For the two processes, the time determinant y is introduced to represent the ratio of the time required for the two processes. We analyze in three cases: y is approximately 1, y is greater than 1 and y is less than 1, and respectively establish optimal scheduling model based on time determinant. The total number of workpieces produced under the three parameters of the solution is 243, 226, 295, and the system operating efficiency is 88%, 82%, and 89%, respectively. For the fault situation, the time is divided into several segments according to the fault point, and we establish the optimal scheduling model for fault reduction dimension based on time segmentation. The total number of workpieces produced in one process is 370, 322, and 378, and the system operation efficiency is as high as 94%, 91%, and 94%. The total number of workpieces produced in two processes is 212, 198, and 250, respectively, and the system operation efficiency is 77%, 72%, and 75%, respectively.
Keywords:Matrix Cycle, Traveling Salesman Problem, Time Determinant, Fault Reduction Dimension, Optimal Scheduling
基于矩阵循环的智能RGV的动态调度策略
顾扬*#,张洲镕†,姜锦†
南京航空航天大学理学院,江苏 南京

收稿日期:2019年2月28日;录用日期:2019年3月12日;发布日期:2019年3月19日

摘 要
本文主要研究一种智能RGV的动态调度问题。针对一道工序的加工作业,通过模拟分析判断出周期循环调度是最优调度。因此建立基于矩阵循环的最优调度模型,将路径规划转化为旅行商问题,利用Lingo、MATLAB求得三组参数条件下工件生产总数分别为384、347、395,系统作业效率均高达98%。针对两道工序,引入时间决定因子y表示两道工序所需时间的比值,分三种情况分析:y近似于1,y大于1和y小于1,分别建立基于时间决定因子的最优调度模型,求解可得三组参数条件下工件生产总数分别为243、226、295,系统作业效率分别达88%、82%、89%。针对故障情况,按照故障点把时间分割成若干片段,建立基于时间分段的故障降维最优调度模型,求解可得一道工序下工件生产总数分别为370、322、378,系统作业效率高达94%、91%、94%;两道工序下工件生产总数分别为212、198、250,系统的作业效率分别达77%、72%、75%。
关键词 :矩阵循环,旅行商问题,时间决定因子,故障降维,最优调度

Copyright © 2019 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
智能加工系统如图1所示,由8台计算机数控机床(Computer Number Controller, CNC)、1辆轨道式自动引导车(Rail Guide Vehicle, RGV)、1条RGV直线轨道、1条上料传送带、1条下料传送带等附属设备组成。RGV是一种无人驾驶、能在固定轨道上自由运行的智能车。它根据指令能自动控制移动方向和距离,并自带一个机械手臂、两只机械手爪和物料清洗槽,能够完成上下料及清洗物料等作业任务。
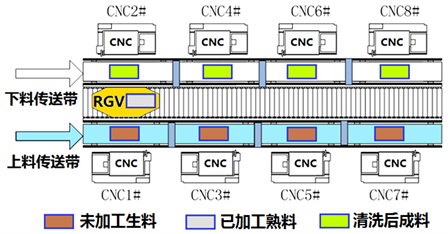
Figure 1. Schematic diagram of smart processing system
图1. 智能加工系统示意图
智能RGV的动态调度问题针对下面三种具体情况:
1) 一道工序的物料加工作业情况,每台CNC安装同样的刀具,物料可以在任一台CNC上加工完成;
2) 两道工序的物料加工作业情况,每个物料的第一和第二道工序分别由两台不同的CNC依次加工完成;
3) CNC在加工过程中可能发生故障(据统计:故障的发生概率约为1%)的情况,每次故障排除(人工处理,未完成的物料报废)时间介于10~20分钟之间,故障排除后即刻加入作业序列。要求分别考虑一道工序和两道工序的物料加工作业情况。
为了解决此问题,本文基于2018年全国大学生数学建模竞赛B题所提供的数据针对下列两项任务展开研究:
任务1:对一般问题进行研究,给出RGV动态调度模型和相应的求解算法;
任务2:利用表1中系统作业参数的3组数据分别检验模型的实用性和算法的有效性,给出RGV的调度策略和系统的作业效率,并得出具体的结果。
Table 1. Three sets of data sheets for smart processing system operating parameters (Time unit: second)
表1. 智能加工系统作业参数的3组数据表(时间单位:秒)
注:每班次连续作业8小时。
2. 问题分析
该问题是对智能加工系统中RGV的动态调度问题,理想的调度策略可以保证系统的作业效率,以高效地满足生产需求。
按照要求在智能系统实际的运作规则下,考虑三种一般问题:
1) 一道工序的物料加工作业;
2) 两道工序的物料加工作业;
3) CNC发生故障情况下一道工序和两道工序的物料加工作业。
建立出RGV动态调度模型,给出相应的求解算法,并利用给出的3组数据系统作业参数分别检验模型的实用性和算法的有效性,给出RGV的调度策略和系统的作业效率。
2.1. 任务一的问题分析
2.1.1. 情况(1)的分析
在分析了智能加工系统的工作流程之后,进行程序模拟只有一道工序的调度过程,发现RGV的调度是周期循环调度,在验证了周期性的合理性后,可判断循环调度即为最优调度。同时,所有CNC完成上下料作业与相应的清洗作业所用总时间都是固定值,因此可将该部分时间消耗看作一个整体,将优化策略体现在RGV的移动顺序上,整个过程就可以简化为单纯的路径规划问题,从寻找最优路径着手,逐步建立调度模型。为此,引入邻接矩阵A和位置矩阵B,可以认为邻接矩阵在每个周期内均为同一状态,于是可以将模型简化,把规划目标转化为RGV调度周期最短,从而基于矩阵循环建立RGV最优调度模型,该模型的求解从根本上可归结为旅行商问题 [1] ,利用Lingo [2] 软件可解出其最优路径,用MATLAB软件 [3] 模拟仿真可得三组参数条件下工件生产总数和系统的作业效率。
2.1.2. 情况(2)的分析
与情况(1)的分析过程类似,程序模拟后发现在两道工序的物料加工作业情况下RGV的调度路线也呈现周期性循环,最优生产效果的关键在于RGV的调度顺序,于是单独考虑一个循环节的调度规划,把RGV调度周期最短作为最终的规划目标。
由于两道工序所需时间之间大小关系不同,其呈现出的周期性特点也不相同,因此需要分三种情况对其周期性特点进行讨论:
1) 两道工序所需时间大小相当;
2) 第一道工序所需时间明显大于第二道;
3) 第一道工序所需时间明显小于第二道。
考虑在模型一的基础上,以两道工序所需时间的比值作为决定因子,建立基于时间决定因子的最优调度模型,用MATLAB模拟一个班次内的调度策略 [4] ,可得三组参数条件下工件生产总数和系统的作业效率。
2.1.3. 情况(3)的分析
在加工过程中一旦有CNC发生故障,可将发生故障时间段截取出来,使一个班次内的时间被分割成若干片段,对于不产生故障的时间段,动态调度策略完全按照情况(1)和情况(2)执行;对于故障段,剔除了故障节点,则邻接矩阵和距离矩阵均进行了降维,可将新状态视为原状态的子状态,但仍然适用于原模型,对新状态下的智能系统重新规划最优循环路径,建立基于时间分段的故障降维最优调度模型。对各段均求解出最优循环路径下子状态的工件生产量,从而得到一个班次内工件生产总量和系统的作业效率。
2.2. 任务二的问题分析
最后,利用题目给出的3组系统作业参数分别对模型求解,同时计算未优化路线下系统的生产总量,使之与模型所求结果进行比较,从而可以检验模型的实用性和算法的有效性,进一步可科学合理地给出三种情况下RGV的调度策略与相应的系统作业效率。
3. 模型假设
经过对问题的分析,提出以下几点假设:
1) RGV在调度过程中运输正常,不会出现偶然事故,且不受其他因素的影响;
2) RGV在上下料、清洗等作业过程中不会出现时间浪费;
3) 熟料在清洗槽中的实际清洗时间很短,忽略不计。
4. 符号说明
A表示RGV的调度路线中n个(本题n = 8) CNC形成的邻接矩阵;
B表示RGV在n个(本题n = 8) CNC之间移动时间形成的位置矩阵;
表示一道工序的物料加工作业情况下RGV调度的最短周期(单位:秒);
表示RGV为CNC2#,4#,6#,8#一次上下料所需时间(单位:秒);
表示RGV为CNC1#,3#,5#,7#一次上下料所需时间(单位:秒);
q表示RGV完成一个物料的清洗作业所需时间(单位:秒);
y表示时间决定因子;
表示CNC加工完成一个两道工序物料的第一道工序所需时间;
CNC加工完成一个两道工序物料的第二道工序所需时间。
表示RGV从 所用时间;
表示RGV从 所用时间;
表示理想情况下一个班次内最多可生产的工件数;
表示系统作业效率;
t表示当前循环最后一个物料下料开始时间。
5. 模型的建立与求解
5.1. 任务一模型的建立
5.1.1. 基于矩阵循环的最优调度模型
分析智能加工系统的组成与作业流程,得知,尽管RGV为偶数编号CNC一次上下料所需时间要大于为奇数编号CNC一次上下料所需时间,并且在RGV为某CNC完成一次上下料作业后,还要对加工完成的熟料进行清洗作业,但综合整个一轮的工作,所有CNC完成上下料作业与相应的清洗作业所用总时间都是固定值,因此可将该部分时间消耗看作一个整体,于是优化策略便体现在RGV的移动顺序上,整个过程就可以简化为单纯的路径规划问题,从寻找最优路径着手,逐步建立最优调度模型 [5] 。于是,引入邻接矩阵A和位置矩阵B。
将RGV的调度路线量化成n个(本题n = 8) CNC形成的邻接矩阵A。
(1.1)
其中,
(1.2)
将RGV在n个(本题n = 8) CNC之间移动的时间量化成位置矩阵B。
(1.3)
其中, 表示RGV从i号CNC移动到j号CNC所用时间, 。
在分析智能加工系统的工作流程之后,不难得出,最好的调度策略是使加工成料总数最多,也就是说使得RGV在移动过程中,CNC的等待时间尽可能短,然而在一段时间内,RGV的调度路线呈周期性循环,于是认为RGV的调度策略采用循环调度具有合理性,而在每一段循环节里,8个CNC全部完成上下料作业和相应的孰料清洗时间都是固定值,可视为一个整体,对优化目标不会产生影响,可将该定值整体视为周期时间的一部分,因此优化目标函数则体现在邻接矩阵A和位置矩阵B之间的运算关系上,同时,已知每一个循环节里邻接矩阵A均为确定状态,而位置矩阵B始终是确定状态,于是可以单独考虑一个循环节的调度规划,把RGV调度周期最短作为最终的规划目标。
在每一个周期内,时间分析可分为两种情况:
1) 工件加工时间大于RGV移动遍历所有CNC、上下料作业和清洗作业总时间;
2) 工件加工时间小于RGV移动遍历所有CNC、上下料作业和清洗作业总时间。
在两种情况下,导致一个周期内RGV返回初始位置的时间点不同,因此要单独考虑RGV回到初始点的移动时间和回到初始点后对初始点CNC的上下料时间。
因此基于循环矩阵的RGV最优调度模型目标函数为:
(1.4)
约束条件为:
(1.5)
其中, 为最短周期, 为RGV为CNC2#,4#,6#,8#一次上下料所需时间, 为RGV为CNC1#,3#,5#,7#一次上下料所需时间,q为RGV完成一个物料的清洗作业所需时间, 表示集合s中元素个数。
5.1.2. 基于时间决定因子的最优调度模型
在情况(1)模型建立的基础上,考虑两道工序的物料加工作业情况,综合分析一个班次内的RGV调度路线,同样发现其呈现周期性循环,而在每一段循环节里,所有CNC全部完成上下料作业和相应的熟料清洗时间都是固定值,可视为一个整体,对优化目标不会产生影响,于是单独考虑一个循环节的调度规划,把RGV调度周期最短作为最终的规划目标。
由于CNC分别加工完成两道工序所需时间的大小关系不同,定义时间决定因子为:
(1.6)
其中,y表示时间决定因子, 表示CNC加工完成一个两道工序物料的第一道工序所需时间, 表示CNC加工完成一个两道工序物料的第二道工序所需时间。
则其周期性特点可分为以下三种情况讨论:
1) 当y近似于1,即两道工序所需时间大小相当,则采用控制加工第二道工序物料CNC个数的方法,根据第二道工序的加工时间采取适当的循环节点数。
截取一个完整循环进行分析,首先在智能系统开始运转时让所有CNC都处于工作状态,即所有CNC此时都在进行第一道工序,经过如图2的调度,最终会出现所有CNC都在进行第一道工序,即出现开始循环,但循环起始节点不一样。
 注:CNC = 1表示在进行第一道工序的加工,CNC = 2表示在进行第二道工序的加工。
注:CNC = 1表示在进行第一道工序的加工,CNC = 2表示在进行第二道工序的加工。
Figure 2. Cycle diagram (1)
图2. 循环示意图(1)
2) 当y大于1,即第一道工序加工时间明显大于第二道工序加工时间,则选取所有CNC均在进行第一道工序的加工为循环节的初始状态,此时从第二道工序到第一道工序切换的优先级高于从第一道工序到第二道工序切换。经过如图3所示的调度过程,则最终一定会出现所有的CNC均进行第一道工序加工的状态,即出现了循环现象。
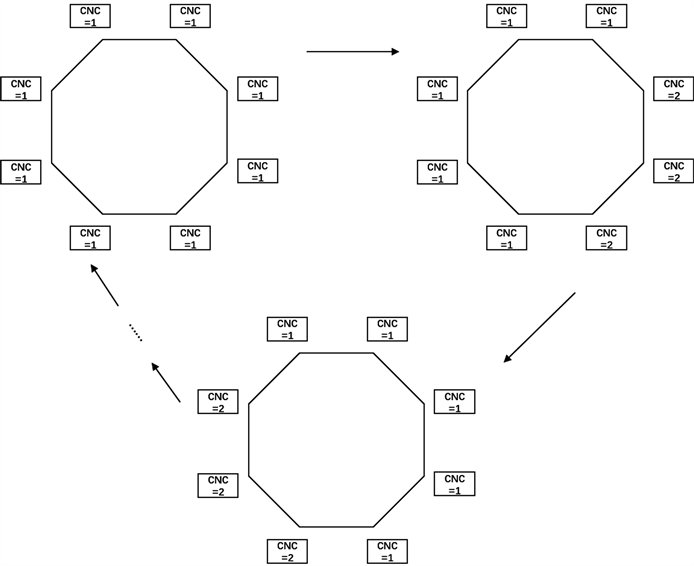
Figure 3. Cycle diagram (2)
图3. 循环示意图(2)
3) 当y小于1,即第一道工序加工时间明显小于第二道工序加工时间,则选取所有CNC均在进行第二道工序的加工为循环节的初始状态,RGV的调度情况与(2)同理,如图4所示,则一定会出现所有的CNC均进行第二道工序加工的状态,即出现了循环现象。
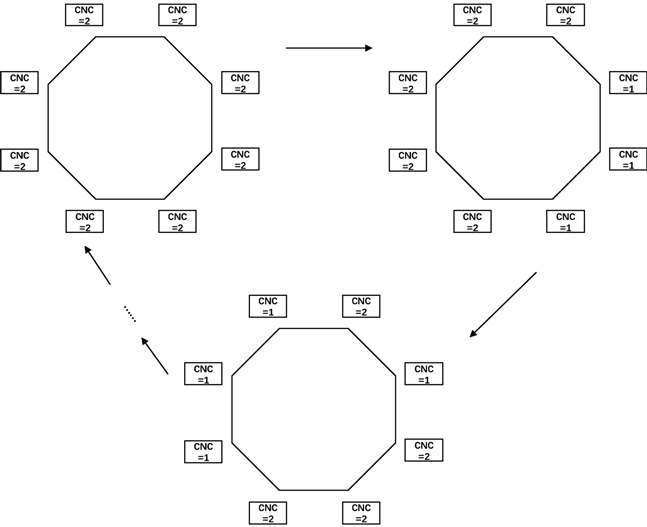
Figure 4. Cycle diagram (3)
图4. 循环示意图(3)
综合以上分析,可得二道工序的物料加工作业下RGV调度模型分别为:
1) 当y近似于1,即两道工序所需时间大小相当时:
目标函数:
(1.7)
约束条件:
(1.8)
2) 当y小于1第一道工序所需时间明显小于第二道时:
在图5中,(a)是事实情景的反映,但由于各个点方格线对建模的影响较大,将(a)改进变形得到(b)。由于各个点的等价性,忽略点在某具体位置,得到空的正八边形。用该图形对问题进行分析,规划,结合数据的特性,得到如图的线路。为了分析路径的段数,将改进(b)得到容易分析的(c)。
针对图5(b),箭头所指路线为:
针对图5(c),路径经过的路线段长为:
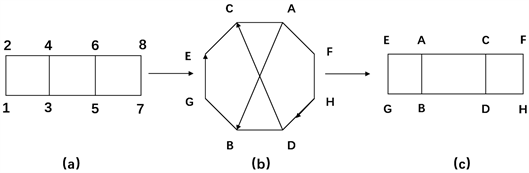
Figure 5. Abstract route (1)
图5. 抽象路线(1)
从而得目标函数:
(1.9)
约束条件:
(1.10)
注: 表示RGV从 所用时间, 表示RGV从 所用时间。
3) 当y大于1,即第一道工序所需时间明显大于第二道时:
同理,如图6所示对循环路线抽象:
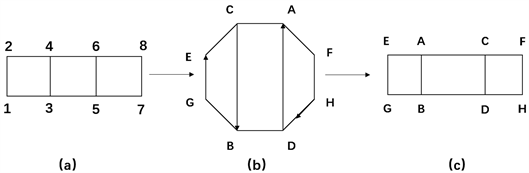
Figure 6. Abstract route (2)
图6. 抽象路线(2)
从而得目标函数:
(1.11)
约束条件:
(1.12)
5.1.3. 基于时间分段的故障降维最优调度模型
CNC在加工过程中可能发生故障(据统计:故障的发生概率约为1%)的情况,每次故障排除(人工处理,未完成的物料报废)时间介于10~20分钟之间,故障排除后即刻加入作业序列。
由分析知,在某一处CNC发生故障后,由于故障时间较长,在发生故障期间,可视其他CNC开始组成新的循环,因此可对情况(1)和情况(2)模型进行推广,一旦有CNC发生故障,将发生故障时间段截取出来,则一个班次内的时间被分割成若干片段。对于无故障发生的时间段,动态调度策略同情况(1)和情况(2);对于故障段,剔除发生故障的节点,则该段循环内邻接矩阵和距离矩阵均发生了降维 [6] ,可将新状态视为原状态的子状态,仍然适用于原模型,对降维后的智能系统运用Lingo软件重新规划最优循环路径,从而可用已有的模型求解出最优循环路径下子状态的工件生产总量。
对于一道工序的物料加工作业,推广后模型的目标函数为:
(1.13)
约束条件为:
(1.14)
其中,n < 8,且8-n表示产生故障的CNC数量。
对于二道工序的物料加工作业,以y近似于1,即两道工序所需时间大小相当的情况为例,推广后的优化模型为:
目标函数:
(1.15)
约束条件:
(1.16)
其中,n < 8,且8 − n表示产生故障的CNC数量。
5.2. 任务二模型的求解
5.2.1. 基于矩阵循环的最优调度模型求解
根据最优调度模型(1.4),为使RGV调度周期最短,必须寻找RGV循环调度的最优路径,从而利用该路径循环模拟一定时间内的RGV调度路线,得出系统的作业效率。求解该最优调度模型的算法步骤如下所示:
Step 1:初始化:将RGV的调度路线量化成 的邻接矩阵A,将RGV在8个CNC之间移动的时间量化成位置矩阵B。
Step 2:求解目标函数:即最优路径的求解,根据RGV调度模型(1.4)数学规划的具体形式,最优路径的求解从根本上来看属于TSP问题,可以使用Lingo软件解决该类问题,从而得出一个循环周期内邻接矩阵A的具体表达形式。
Step 3:判断:利用Step 2中所得的邻接矩阵A,用Matlab软件模拟一个班次(即8小时)内RGV的循环调度过程,若当前上下料开始时间大于28,800秒,则退出循环。
Step 4:输出结果:输出一个班次内RGV的调度策略,从而得出该时段内生产工件的总数n。
Step 5:计算系统的作业效率:理想情况下,一个最短循环周期内完成8个工件的加工是最高效的,从而一个班次内最多可生产的工件数为:
(1.17)
其中, 表示理想情况下一个班次内最多可生产的工件数, 表示最短循环周期。
由此定义所要求的系统作业效率为:
(1.18)
根据如图7所示的算法流程对模型进行求解,分别得到三组参数的加工作业数据结果。
以第一组数据为例,用Lingo软件可得到邻接矩阵为:
(1.19)
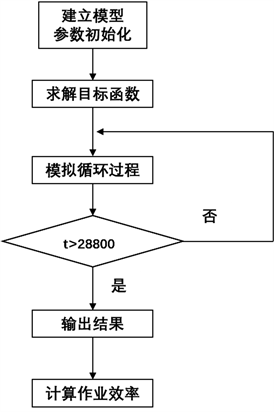 注:t表示当前循环最后一个物料下料开始时间。
注:t表示当前循环最后一个物料下料开始时间。
Figure 7. Algorithm flowchart of Model 1
图7. 模型一算法流程图
通过MATLAB上的模拟结果可知,该时段内共可生产工件384个,同时系统的作业效率高达98%。
从而RGV的具体调度策略和系统的作业效率如下表2所示:
Table 2. Scheduling strategy of RGV and system operating efficiency
表2. RGV的调度策略和系统的作业效率
5.2.2. 基于时间决定因子的最优调度模型求解
两道工序的物料加工作业情况下RGV的调度路线也呈现周期性循环,最优生产效果的关键在于RGV的调度顺序,于是单独考虑一个循环节的调度规划,把RGV调度周期最短作为最终的规划目标。
Step 1:穷举路线:因为Lingo的局限性,采用穷举算法得到所有的路线排序。
Step 2:求解目标函数:根据约束条件,用穷举产生的所有排序求解目标函数,得到最优解,即是最优排序。
Step 3:判断:模拟一个班次(即8小时)内RGV的循环调度过程,若当前上下料开始时间大于28,800秒,则退出循环。
Step 4:输出结果:输出一个班次内RGV的调度策略,从而得出该时段内生产工件的总数n。
Step 5:计算系统的作业效率:理想情况下,一个最短循环周期内完成8个工件的加工是最高效的,从而一个班次内最多可生产的工件数和作业效率分别为:
(1.20)
(1.21)
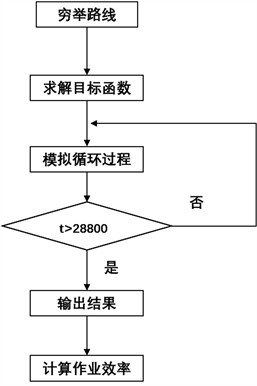
Figure 8. Algorithm flowchart of Model 2
图8. 模型二算法流程图
根据如图8所示的算法流程对模型进行求解,分别得到三组参数的加工作业数据结果。从而RGV的具体调度策略和系统的作业效率如下表3所示:
Table 3. Scheduling strategy of RGV and system operating efficiency in two processes
表3. 两道工序时RGV的调度策略和系统的作业效率
5.2.3. 基于时间分段的故障降维最优调度模型求解
一旦有CNC发生故障,将发生故障时间段截取出来,则一个班次内的时间被分割成若干片段,对每一段根据相应的最优调度模型,寻找RGV循环调度的最优路径,从而利用该路径循环模拟一定时间内的RGV调度路线,得出系统的作业效率。求解该最优调度模型的算法步骤如下所示:
Step 1:初始化:将RGV的调度路线量化成 的邻接矩阵A,将RGV在8个CNC之间移动的时间量化成位置矩阵B。
Step 2:班次时间分段:以1%为故障发生概率随机生成故障点,使故障点均匀的分布在n个加工成品之间,由故障点将一个班次时间分成若干片段。
Step 3:求解目标函数:对于无故障时间段,最优循环路径不变,对于故障段,对降维后的系统按照相应的最优调度模型求解,重新求解最优路径。
Step 4:判断:模拟一个班次(即8小时)内RGV的循环调度过程,若当前上下料开始时间大于28,800秒,则退出循环。
Step 5:输出结果:输出一个班次内RGV的调度策略,从而得出该时段内生产工件的总数n。
Step 6:计算系统的作业效率:理想情况下,一个最短循环周期内完成8个工件的加工是最高效的,从而一个班次内最多可生产的工件数和作业效率分别为:
(1.20)
(1.21)
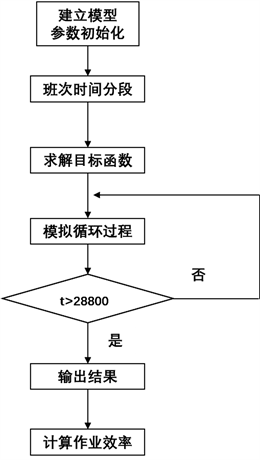
Figure 9. Algorithm flowchart of Model 3
图9. 模型三算法流程图
根据如图9所示的算法流程对模型进行求解,分别得到三组参数的加工作业数据结果。从而RGV的具体调度策略和系统的作业效率如下表4、表5所示:
Table 4. Scheduling strategy of RGV and system operating efficiency in one process in case of failure
表4. 故障情况下一道工序时RGV的调度策略和系统的作业效率
Table 5. Scheduling strategy of RGV and system operating efficiency in two processes in case of failure
表5. 故障情况下两道工序时RGV的调度策略和系统的作业效率
6. 总结
本文所建立的RGV最优调度模型能有效解决题中智能系统的调度问题。该方法可以有效地运用于诸如机械系统、航班调度等优化设计当中。
文章引用
顾 扬,张洲镕,姜 锦. 基于矩阵循环的智能RGV的动态调度策略
Dynamic Scheduling Strategy of Smart RGV Based on Matrix Cycle[J]. 应用数学进展, 2019, 08(03): 481-495. https://doi.org/10.12677/AAM.2019.83054
参考文献
- 1. Bhargava, A. 算法图解[M]. 袁国忠, 译. 北京: 人民邮电出版社, 2017.
- 2. 司守奎, 孙玺菁. LINGO软件及应用[M]. 北京: 国防工业出版社, 2017.
- 3. 张平. Matlab基础与应用[M]. 北京: 北京航空航天大学出版社, 2007.
- 4. 史峰, 王辉. Matlab智能算法30个案例分析[M]. 北京: 北京航空航天大学出版社, 2011.
- 5. 王燕军, 梁治安. 最优化基础理论与方法[M]. 上海: 复旦大学出版社, 2011.
- 6. 张贤达. 矩阵分析与应用[M]. 第2版. 北京: 清华大学出版社, 2013.
NOTES
*第一作者。
#通讯作者。
†共同第二作者。
