Advances in Applied Mathematics
Vol.
09
No.
01
(
2020
), Article ID:
33972
,
4
pages
10.12677/AAM.2020.91013
The Maximum Number of Hyperedges of An r-Uniform D-Hypergraph
Yiping Zhu, Yaping Xiong
School of Mathematics and Statistics, Shandong Normal University, Jinan Shandong

Received: Dec. 26th, 2019; accepted: Jan. 8th, 2020; published: Jan. 15th, 2020

ABSTRACT
A mixed hypergraph on a finite set X is a triple
, where C and D are families of subset of X. The member of C is called C-edge and the member of D is called D-edge. A mixed hypergraph is called C-hypergraph when
, a mixed hypergraph is called D-hypergraph when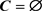 . Let
be a mixed hypergraph, r is a positive integer not less than 2. For an arbitrary C-edge and D-edge, if we have
,, then the mixed hypergraph H is called r-uniform mixed hypergraph. In particular, if
. Let
be a mixed hypergraph, r is a positive integer not less than 2. For an arbitrary C-edge and D-edge, if we have
,, then the mixed hypergraph H is called r-uniform mixed hypergraph. In particular, if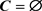 , the mixed hypergraph H is called r-uniform mixed D-hypergraph. In this paper, we solve the problem about the maximum number of hyperedges of an r-uniform D-hypergraph when
, the mixed hypergraph H is called r-uniform mixed D-hypergraph. In this paper, we solve the problem about the maximum number of hyperedges of an r-uniform D-hypergraph when
Keywords:Mixed Hypergraph, r-Uniform D-Hypergraph, The Maximum Number of Hyperedges

r-一致D-超图的最大边数
朱义坪,熊亚萍
山东师范大学数学与统计学院,山东 济南

收稿日期:2019年12月26日;录用日期:2020年1月8日;发布日期:2020年1月15日

摘 要
混合超图
是一个三元组,其中X为H的顶点集。C为X的子集族,记作C-边。D为X的子集族,记作D-边。
的混合超图称为D-超图,
的混合超图称为C-超图。
是一混合超图,r是不小于2的正整数,若满足对任意的C-超边和D-超边,都有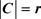 ,
, ,则称混合超图H为r-一致混合超图。特别地,若又有
,则称混合超图H为r-一致混合超图。特别地,若又有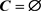 ,则称混合超图H为r-一致D超图。在本文中,我们解决当
时,r-一致D-超图H的最大边数这一问题。
,则称混合超图H为r-一致D超图。在本文中,我们解决当
时,r-一致D-超图H的最大边数这一问题。
关键词 :混合超图,r-一致D-超图,最大超边数

Copyright © 2020 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
1995年,Vitaly Voloshin [1] 对于超图的染色理论提出了其对偶问题,即:使某些超边中至少有两个点染相同的颜色,此类超边称为C-边,传统超边称为D-边,同时包含C-边和D-边的超图称为混合超图,记为
。这两种超图的主要区别体现在染色上。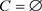 的混合超图称为D-超图,
的混合超图称为D-超图, 的混合超图称为C-超图。
的混合超图称为C-超图。
设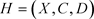 是一混合超图,H的一个正常的k-染色是一个映射
:
,使得下述条件成立:
是一混合超图,H的一个正常的k-染色是一个映射
:
,使得下述条件成立:
1) 每条C-边中至少有两个顶点染相同的颜色;
2) 每条D-边中至少有两个顶点染不同的颜色。
混合超图 的一个k色严格染色是一个正常的k-染色且恰使用了k种染色。使混合超图 有一个严格染色所需的最多(最少)的颜色数被称为H的上色数(下色数),记作 ( )。
混合超图的概念一经提出,关于混合超图的新的问题也随之产生,如对C-超图的染色的研究。C-超图的染色理论是最大顶点染色理论,因为对于C-超图来说,存在1色严格染色。而在超图中所用的最多颜色数即为超图的顶点数,故超图的染色理论是最小顶点染色理论。因此,对于混合超图来说,最小最大顶点染色理论都是有意义的。对于D-超图的染色问题已有许多结果,本文中我们将研究r-一致D-超图,我们首先给出r-一致D-超图的概念:
设
是一混合超图,r是不小于2的正整数,若满足对任意的C-超边和D-超边,都有
,
,则称混合超图H为r-一致混合超图。特别地,若又有
(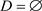 ),则称H为r-一致D-超图(r-一致C-超图)。
),则称H为r-一致D-超图(r-一致C-超图)。
极值问题在超图与混合超图中是有趣的而又极具挑战性的。在参考文献 [1] [2] [3] [4] 中已有一些关于混合超图的最小点数,最小边数等问题的结果。Vitaly Voloshin 在文献 [3] 中提出一个公开问题:当 时,r-一致C-超图H的最大边数是多少?该问题已经在文献 [5] 中得到解决。在本文中,我们解决当 时,r-一致D-超图H的最大边数这一问题。
2. 定理及其证明
定理1 设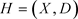 是具有n个顶点的r-一致D-超图,
是顶点集X的一个k-染色且
。则H的最大边数为
,其中r充分大时,对任意的
,
。
是具有n个顶点的r-一致D-超图,
是顶点集X的一个k-染色且
。则H的最大边数为
,其中r充分大时,对任意的
,
。
断言1 存在 使得 。
因为 。当 时,函数 取得最小值。将p代入上面的函数,若
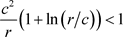
则断言1成立。当r充分大时,对任意的 , ,这个不等式是成立的。因此,断言1的证明完成。
设
具有
条边且p满足上述条件。首先我们随机地用 中的一种颜色逐个给H的顶点着色。其次对于每个顶点v,我们抛掷硬币,出现正面的概率为p。另外,对V中的顶点随机排序。
中的一种颜色逐个给H的顶点着色。其次对于每个顶点v,我们抛掷硬币,出现正面的概率为p。另外,对V中的顶点随机排序。
步骤1. 随机地用 中的一种颜色逐个给H的顶点着色,称之为第一次染色。令B表示位于某条(可能多条)单色边 中的点 的集合。
步骤2. 按V中顶点的顺序依次考虑B中的元素。当我们考虑b时,若存在某条(可能多条)包含b的边 在第一次染色中是单色的且这条边中至今没有顶点改变颜色,则称b仍然危险。若b不是仍然危险的,则保持原有染色。但若b是仍然危险的,则抛掷硬币。若出现正面则改变b的颜色,否则保持原有染色。我们称终止时的染色为最终染色。
坏事件 在最终的染色中,某条边 是单色的。
是单色的。
在最终的染色中,边
是单色的有两种情况。要么在第一次染色中,边e是单色的且在最终的染色中,边e仍然是单色的;要么在第一次染色中,边e不是单色的但在最终的染色中,边e是单色的。第一种情况记作
,第二种情况记作
。在第一次染色中,边e是单色的概率为
,在最终的染色中,所有的硬币出现反面的概率为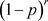 ,即边e仍然是单色的概率为
,则
,即边e仍然是单色的概率为
,则
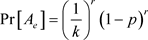
故
为了避免过度重染且得到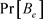 更好的界,我们巧妙地界定
。对于不同的边
,若
更好的界,我们巧妙地界定
。对于不同的边
,若
1) 边 恰重叠一个元素,记作v;
2) 在第一次染色中边f是单色的且在最终的染色中e是单色的;
3) 在步骤2中,点v是边e中最后一个改变颜色的点;
4) 当考虑点v时,边f仍然是单色的;
则称边e取决于边f。
假设
成立。因边e中的某些点会改变染色,故存在最后一个改变颜色的点v。但对于点v,为什么仍要抛掷硬币?因为点v一定存在于某条(可能多条)边f中,边f在第一次染色中是单色的且当考虑点v时,边f仍然是单色的。那么边
会重叠另一个点
?答案是否定的。因为点
一定在点v之前改变颜色,则当考虑点v时,边f不再是完全单色的,与边f的假设矛盾。因此当
成立时,边e取决于边f。令
表示事件边e取决于边f,则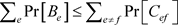 。
。
设边 固定且 (否则 不发生)。顶点集V的随机排序导致了 的一个随机排序 。令 ( )表示在点v之前点 的数量, 表示在点v之前的点 的数量。
由上述讨论知,计算
须同时满足以下几点。首先,在第一次染色中,边f是单色的,在最终的染色中,点v一定会改变颜色。其次,对点v之前的点
进行抛掷硬币时全部是反面朝上。再者,点v之后的点
的颜色起初就相同(因为点v是边e中最后一个改变颜色的顶点)。最后,随机从
中选择颜色对点v之前的点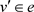 进行染色且最终染色与点v之后的顶点颜色相同。
进行染色且最终染色与点v之后的顶点颜色相同。
固定 得到
得到
故
引理4 [6] 。
因为至多存在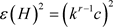 对边
且边
,则
对边
且边
,则
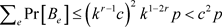
因此坏事件出现的概率为 。由断言1,坏事件不发生的概率为正。这表明存在一种无单色边e的染色。因此,定理1的证明完成。
致谢
感谢导师蔡建生教授给我们介绍混合超图的相关知识,并对本文进行了全面的修改。最后,向各位尊敬的评审专家致以诚挚的感谢,谢谢你们对本论文做出的评审以及提出的宝贵意见。
文章引用
朱义坪,熊亚萍. r-一致D-超图的最大边数
The Maximum Number of Hyperedges of An r-Uniform D-Hypergraph[J]. 应用数学进展, 2020, 09(01): 105-108. https://doi.org/10.12677/AAM.2020.91013
参考文献
- 1. Voloshin, V.I. (2002) Coloring Mixed Hypergraphs: Theory, Algorithms and Applications, AMS, Providence.
- 2. Bujt´as, C. and Tuza, Z. (2008) Uniform Mixed Hypergraphs: The Possible Numbers of Colors. Graphs and Combinatorics, 24, 1-12.
https://doi.org/10.1007/s00373-007-0765-5 - 3. Diao, K., Zhao, P. and Wang, K. (2014) The Smallest One-Realization of a Given Set III. Graphs and Combinatorics, 30, 875-885.
https://doi.org/10.1007/s00373-013-1322-z - 4. Voloshin, V.I. (1992) On the Upper Chromatic Number of a Hypergraph. Scientific Research Conference of the Moldova State University, Theses of Resports, Kishinev, Vol. 1, 42.
- 5. Cai, J., Xiong, Y. and Yang, D. (2020) A Note on the Maximum Number of Hyperedge so f C-Hypergraph. Submitted for Publication.
- 6. Alon, N. and Spencer, J.H. (2008) The Probablistic Method. 3rd Edition, John Wiley and Sons, New York.